13. Условие параллельности прямых на плоскости, заданных общими уравнениями.

Уравнение

Ах+Ву+С=0

(где А, В, Смогут иметь любые значения, лишь бы коэффициентыА, Вне были нулями оба сразу) представляетпрямую линию. Всякую прямую можно представить уравнением этого вида. Поэтому его называютобщим уравнением прямой.

Если А=0, то есть уравнение не содержитх, то оно представляет прямую,параллельную оси ОХ.

Если В=0, то есть уравнение не содержиту, то оно представляет прямую,параллельную оси ОY.

Когла Вне равно нулю, то общее уравнение прямой можноразрешить относительно ординаты у, тогда оно преобразуется к виду

y=ax+b

(где a=-A/B; b=-C/B).

Аналогично, при Аотличным от нуля общее уравнение прямой можно разрешить относительнох.

Если С=0, то есть общее уравнение прямой не содержит свободного члена, то оно представляет прямую, проходящую через начало координат

14. Условие перпендикулярности прямых на плоскости, заданных уравнениями с угловым коэффициентом.

15. Условие перпендикулярности прямых на плоскости, заданных общими уравнениями.

16. Исследование взаимного расположения пар прямых на плоскости, заданных общими уравнениями.

17. Нахождение координат точки пересечения прямых на плоскости.

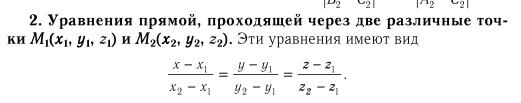
18. Расстояние от данной точки до данной прямой на плоскости.

С =>

18. Линейное уравнение, определение решения линейного уравнения. Равносильность линейных уравнений. Противоречивые и тривиальные уравнения. Общий вид решения уравнения.

Линейное уравнение с одной переменной x – это уравнение вида a·x+b=0, где a и b – некоторые числа, называемые коэффициентами линейного уравнения.

определение решения линейного уравнения: перенос слагаемого из одной части уравнения в другую с противоположным знаком, а также умножение или деление обе частей уравнения на одно и то же отличное от нуля число.

два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

модель — система уравнений и неравенств — противоречива, что нельзя подобрать такие числовые значения неизвестных, при которых выполнялись бы одновременно все уравнения и неравенства. Тривиальное уравнение имеет нулевое решение.

18. Системы линейных уравнений: определение решения системы линейных уравнений. Свойства систем уравнений: совместность, несовместность, определенность, неопределенность. Аналогия с исследованием взаимного расположения двух прямых на плоскости.

Решением системы линейных алгебраических уравнений называют набор значений неизвестных переменных, обращающий все уравнения системы в тождества. 1) Пусть нам требуется решить систему линейных алгебраических уравнений, в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля.

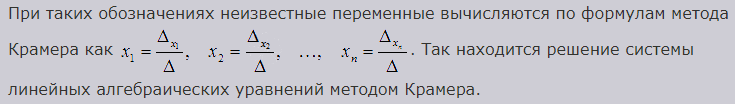2)

Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x1 из всех уравнений системы, начиная со второго, далее исключается x2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная xn. Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находится xn, с помощью этого значения из предпоследнего уравнения вычисляется xn-1, и так далее, из первого уравнения находится x1. Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса.

Свойства систем уравнений: совместность, несовместность, определенность, неопределенность.

Если система уравнений имеет хотя бы одно решение, то она называется совместной. Если система уравнений решений не имеет, то она называется несовместной. Если СЛАУ имеет единственное решение, то ее называют определенной; если решений больше одного, то – неопределенной.

Аналогия с исследованием взаимного расположения двух прямых на плоскости.

Нахождение координат точки пересечения двух прямых. Координаты должны одновременно удовлетворять уравнениям обеих прямых, т.е. системе.