8. Прямая на плоскости: уравнение прямой в отрезках.

Уравнение прямой в отрезках

Уравнение (**), где все А, В, С отличны от нуля, можно привести к виду:

Действительно,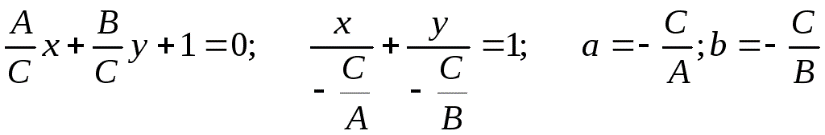 

Числа а и b имеют простой геометрический смысл: это отрезки осей координат, которые отсекает прямая линия, удовлетворяющая этому уравнению.

Действительно, при х = 0 : 

при у = 0 : х = а

9.Общее уравнение прямой и его исследование

Теорема: В декартовой прямоугольной системе координат Oxy на плоскости любая прямая может быть задана уравнением первой степени относительно x и y:

Аx+By+C=0 (1)

Где A,B,C – постоянные числа, причем A² + B² > 0 и обратно, всякое уравнение вида (1) определяет прямую. Вектор n = (A,B) перпендикулярен к прямой (1) и называется нормальным вектором прямой. Само уравнение называется общим уравнением прямой. Если В не равно 0, то уравнение можно представить в виде y=kx+b (k=tg α). Последнее уравнение называется уравнением прямой с угловым коэффициентом.

10. Построение прямой на плоскости по его уравнению. Чтобы построить прямую линию, достаточна нанести на чертеж две какие-нибудь ее точки. Для отыскания координат какой-либо точки, лежащей на прямой, выбираем произвольно значение одной из координат и по уравнению прямой находим соответствующее значение второй координаты.

Пример 1. Построить прямую, заданную уравнением

Положим, например,  тогда  или  Следовательно, точка  лежит на прямой. Аналогично, полагал, например,  найдем точку  также лежащую на прямой. Двумя найденными точками определяется прямая (рис. 44).

Пример 2. Построить прямую 

Так как в уравнении  отсутствует свободный член, то, прямая, определяемая этим уравнением, проходит через начало координат. Чтобы найти точку прямой, отличную от начала, положим  равным, например, 1; тогда или 

Следовательно, точка 1, — лежит на прямой. Остается провести прямую через эту точку и начало координат.

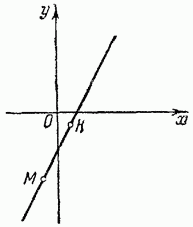
Рис. 44.

Замечание. Практически при построении прямой удобно использовать уравнение в отрезках, или найти точки пересечения прямой с осями координат.

11. Определение угла между двумя прямыми на плоскости. Угол между прямыми на плоскости

Определение. Если заданы две прямые y = k₁ x + b₁ , y = k₂x + b₂ , то острый угол между этими прямыми будет определяться как

 

.

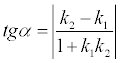Две прямые параллельны, если k₁ = k₂ . Две прямые перпендикулярны, если k₁ = -1/ k₂ .

Теорема. Прямые Ах + Ву + С = 0 и А ₁ х + В₁ у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = λА, В₁ = λВ. Если еще и С₁ = λС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

 

Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой

Определение. Прямая, проходящая через точку М₁ (х₁ , у₁ ) и перпендикулярная к прямой у = kx + b представляется уравнением:

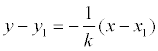
12. Условие параллельности прямых на плоскости, заданных уравнениями с угловым коэффициентом.

В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую.

Уравнение вида

 (1)

называется общим уравнением прямой.

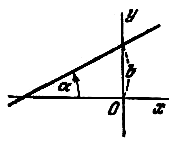
Угол , определяемый, как показано на рис., называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:

Уравнение  называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением

,

то ее угловой коэффициент определяется по формуле

.

Уравнение  является уравнением прямой, которая проходит через точку  (, ) и имеет угловой коэффициент k.

Если прямая проходит через точки (, ), (, ), то ее угловой коэффициент определяется по формуле

.

Уравнение

является уравнением прямой, проходящей через две точки (, ) и (, ).

Если известны угловые коэффициенты  и  двух прямых, то один из углов  между этими прямыми определяется по формуле

.

Признаком параллельности двух прямых является равенство их угловых коэффициентов:.

Признаком перпендикулярности двух прямых является соотношение , или .

Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.