45 Уравнение прямой в пространстве, проходящее через две различные данные точки.

Аналитическая геометрия

Уравнение прямой, проходящей через две данные точки.

Пусть на плоскости даны М1(х1у1) и М2(х2у2). Составим каноническое уравнение прямой, проходящей через эти две точки в качестве направляющего вектора S возьмем M1M2

тройка.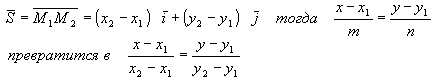

- это уравнение прямой, проходящей через две данные точки (х1 у1) и (х2, у2)

Перейдем теперь к уравнениям прямой и плоскости в пространстве.

Аналитическая геометрия в 3-мерном пространстве

Аналогично двумерному случаю любое уравнение первой степени относительно трех переменных x, y, z есть уравнение плоскости в пространстве Оxyz.. Общее уравнение плоскости АX + ВY + СZ + D = 0, где вектор N=(A,B,C) есть нормаль к плоскости. Каноническое уравнение плоскости, проходящей через точку М(х0,у0,z0) и имеющей нормаль N(А,В,С) А(х – х0) + В(у – у0) + С(z – z0)=0 – что представляет собой это уравнение?

Значения х –х0, у-у0 и z –z0 — это разности координат текущей точки и фиксированной точки. Следовательно, вектор а (х-х 0, у-у0, z-z0) -это вектор, лежащий в описываемой плоскости, а вектор N — вектор, перпендикулярный к плоскости, а значит, они перпендикулярны между собой.

Тогда их скалярное произведение должно равняться нулю.

В координатной форме (N,a)=0 выглядит так:

А·(х-х0)+В·(у-у0)+С·(z-z0)=0

В пространстве различают правые и левые тройки векторов. Тройка некомпланарных векторов а, b, с называется правой, если наблюдателю из их общего начала обход концов векторов a, b, с в указанном порядке кажется совершающимся по часовой стрелке. В противном случае a,b,c - левая .

61. Условия параллельности и перпендикулярности двух прямых в пространстве.

Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т. е. их соответствующие координаты были пропорциональны.

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т. е. косинус угла между ними равен нулю.

62. Условия параллельности и перпендикулярности прямой и плоскости в пространстве.

Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.

Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарные. Это условие выполняется, если векторное произведение этих векторов было равно нулю.