
- •1. Предмет и метод аналитической геометрии. Начальные понятия геометрии.
- •2. Направленные отрезки на оси. Величина направленного отрезка. Линейные операции над направленными отрезками.
- •8. Прямая на плоскости: уравнение прямой в отрезках.
- •9.Общее уравнение прямой и его исследование
- •11. Определение угла между двумя прямыми на плоскости. Угол между прямыми на плоскости
- •Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- •12. Условие параллельности прямых на плоскости, заданных уравнениями с угловым коэффициентом.
- •13. Условие параллельности прямых на плоскости, заданных общими уравнениями.
- •21. Эквивалентность систем линейных уравнений. Элементарные преобразования систем, приводящие к эквивалентным системам линейных уравнений.
- •22. Метод Гаусса решения систем линейных уравнений (метод исключения переменных). Основные шаги, прямой и обратный ход метода.
- •Формулы прямого хода
- •Обратный ход
- •23. Три варианта завершения прямого хода метода Гаусса: а) система несовместная, б) система совместная и неопределенная; в) система совместная и определенная.
- •24. Общее и частное решение системы линейных уравнений. Привести пример. Фундаментальная система решений.
- •25. Матрицы, операции над ними и их свойства: сложение матриц, умножение матрицы на число (произведение матрицы на число), транспонирование матриц.
- •26. Произведение матриц: умножение матрицы строки на матрицу-столбец; умножение матрицы на столбец; умножение строки на матрицу; умножение матриц.
- •27. Условия существования произведения матриц. Свойства операции умножения матриц.
- •Возведение матрицы в степень, условие существования степени матрицы.
- •Понятие определителя матрицы. Формулы для вычисления определителей 2-го и третьего порядков. Свойства определителя.
- •Формулы Крамера для решения систем линейных уравнений. Исследование систем с определителем, равным нулю.
- •Миноры и алгебраические дополнения, их связь с определителем матрицы. Вычисление определителей методом разложения по строке или столбцу.
- •32. Обратная матрица: определение, условие существования. Присоединенная матрица.
- •33. Алгоритм вычисления обратной матрицы.
- •34. Решение систем линейных уравнений с использованием обратной матрицы.
- •35. Ранг матрицы и его свойства. Алгоритм вычисления ранга матрицы.
- •36. Исследование систем линейных уравнений с использованием теоремы Кронекера-Капелли.
- •37. Базисное решение. Однородные и неоднородные системы линейных уравнений.
- •38. Векторы на плоскости и в пространстве: определение, параллельный перенос, равенство векторов. Классы равных векторов. Коллинеарные и компланарные векторы.
- •39. Операции над векторами и их свойства
- •40. Направляющие косинусы Формула вычисления направляющих косинусов вектора для плоских задач
- •Формула вычисления направляющих косинусов вектора для пространственных задач
- •41. Координаты вектора. Декартова система координат в пространстве. Радиус-векторы: взаимнооднозначное соответствие между точками и направленными отрезками. Связь координат коллинеарных векторов.
- •42. Линейно зависимые системы векторов и их свойства.
- •43. Линейно независимые системы векторов и их свойства.
- •44.Ранг и базис системы векторов. Разложение вектора по базису.
- •46. Линейная зависимость и системы линейных уравнений. Связь ранга матрицы с базисом системы векторов.
- •47. Общее уравнение кривой второго порядка. Определение вида кривой второго порядка по коэффициентам ее уравнения.
- •Определение окружности. Каноническое уравнение окружности. Приведения общего уравнения окружности к каноническому.
- •Определение эллипса. Каноническое уравнение эллипса. Приведение общего уравнения эллипса к каноническому.
- •Координаты фокусов эллипса и его эксцентриситет.
- •51. Гипербола: определение. Общее и каноническое уравнения гиперболы. Координаты фокусов гиперболы и уравнения его асимптот.
- •Определение параболы. Каноническое уравнение параболы. Приведение общего уравнения параболы к каноническому.
- •53. Координаты вершины и фокуса параболы. Уравнение директрисы параболы.
- •54. Скалярное произведение векторов и его свойства.
- •55. Выражение скалярного произведения в декартовых координатах. Необходимое и достаточное условие ортогональности векторов. Нормальный вектор прямой (на плоскости) и плоскости (в пространстве).
- •56. Векторное произведение векторов и его свойства.
- •57. Смешанной произведение векторов и его свойство.
- •58. Общее уравнение плоскости в пространстве. Уравнение плоскости в отрезках. Общее уравнение плоскости в пространстве
- •59. Условия параллельности и перпендикулярности двух плоскостей в пространстве.
- •60. Общие уравнения прямой в пространстве. Канонические уравнения прямой в пространстве. Уравнения прямой в пространстве, проходящей через две точки.
- •44 Параметрические уравнения прямой
- •45 Уравнение прямой в пространстве, проходящее через две различные данные точки.
- •61. Условия параллельности и перпендикулярности двух прямых в пространстве.
- •62. Условия параллельности и перпендикулярности прямой и плоскости в пространстве.
56. Векторное произведение векторов и его свойства.
Векторным
произведением двух векторов ![]() и
и ![]() ,
заданных в прямоугольной системе
координат трехмерного пространства,
называется такой вектор
,
заданных в прямоугольной системе
координат трехмерного пространства,
называется такой вектор ![]() ,
что
,
что
-
он является нулевым, если векторы
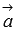 и
и 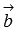 коллинеарны;
коллинеарны; -
он перпендикулярен и вектору
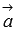 и
вектору
и
вектору 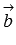 (
(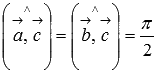 );
); -
его длина равна произведению длин векторов
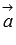 и
и 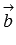 на
синус угла между ними (
на
синус угла между ними (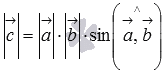 );
); -
тройка векторов
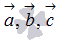 ориентирована
так же, как и заданная система координат.
ориентирована
так же, как и заданная система координат.
свойства векторного произведения:
-
антикоммутативность
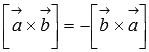 ;
; -
свойство дистрибутивности
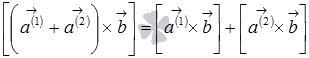 или
или 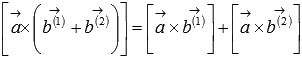 ;
; -
сочетательное свойство
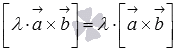 или
или 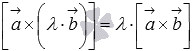 ,
где
,
где 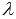 -
произвольное действительное число.
-
произвольное действительное число.
57. Смешанной произведение векторов и его свойство.
Смешанным
произведением трех векторов ![]() и
и ![]() называется
действительное число, равное скалярному
произведению векторов
называется
действительное число, равное скалярному
произведению векторов 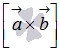 и
и ![]() ,
где
,
где 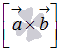 -
векторное произведение векторов
-
векторное произведение векторов ![]() и
и ![]() .
.
свойства смешанного произведения:
-
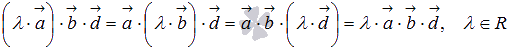 ;
; -
 ;
; -
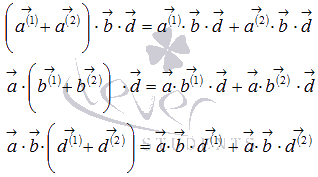
58. Общее уравнение плоскости в пространстве. Уравнение плоскости в отрезках. Общее уравнение плоскости в пространстве
![]() –
общее
уравнение плоскости в пространстве
–
общее
уравнение плоскости в пространстве
Нормальный вектор плоскости
Нормальным вектором плоскости назовем ненулевой вектор, ортогональный каждому вектору, лежащему в плоскости.
Уравнение
плоскости, проходящей через точку![]() с
заданным вектором нормали
с
заданным вектором нормали
![]() –
уравнение
плоскости, проходящей через точку M0 с
заданным вектором нормали
–
уравнение
плоскости, проходящей через точку M0 с
заданным вектором нормали
Направляющие векторы плоскости
Два неколлинеарных вектора, параллельных плоскости, назовем направляющими векторами плоскости
Параметрические уравнения плоскости
![]() –
параметрическое
уравнение плоскости в векторном виде
–
параметрическое
уравнение плоскости в векторном виде
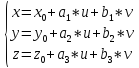 –
параметрическое
уравнение плоскости в координатах
–
параметрическое
уравнение плоскости в координатах
Уравнение плоскости через заданную точку и два направляющих вектора
![]()
![]()
![]() –фиксированная
точка
–фиксированная
точка
![]() –просто
точка лол
–просто
точка лол
![]() –компланарные,
значит их смешанное произведение равно
0.
–компланарные,
значит их смешанное произведение равно
0.
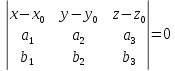
Уравнение плоскости, проходящей через три заданные точки
![]()
![]()
![]()
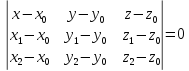 –
уравнение
плоскости через три точки
–
уравнение
плоскости через три точки
Уравнение плоскости в отрезках
![]()
![]()
![]()
![]() –
уравнение
плоскости в отрезках
–
уравнение
плоскости в отрезках
59. Условия параллельности и перпендикулярности двух плоскостей в пространстве.
Даны две плоскости, заданные общими уравнениями:
A1x + B1y + C1z + D1 = 0,
A2x + B2y + C2z + D2 = 0.
Они имеют нормальные векторы:
![]() 1(A1, B1, C1),
1(A1, B1, C1),
![]() 2(A2, B2, C2).
2(A2, B2, C2).
1. Если плоскости параллельны, то векторы нормалей коллинеарны.
![]() -
условие параллельности плоскостей.
-
условие параллельности плоскостей.
2. Если плоскости перпендикулярны, то векторы нормалей ортогональны.
![]() 1
1 ![]() 2 =
0,
2 =
0,
A1A2 + B1B2 + C1C2 = 0 - условие перпендикулярности плоскостей.
60. Общие уравнения прямой в пространстве. Канонические уравнения прямой в пространстве. Уравнения прямой в пространстве, проходящей через две точки.
Пусть прямая проходит через точку M1 (x1, y1, z1) и параллельна вектору (m ,n, l). Составим уравнение этой прямой.
Возьмем
произвольную точку M (x, y, z) на этой прямой
и найдем зависимость между x, y, z. Построим
вектор ![]()
Векторы ![]() и
и![]() коллинеарны.
коллинеарны.
![]() -
каноническое уравнение прямой в
пространстве.
-
каноническое уравнение прямой в
пространстве.
44 Параметрические уравнения прямой
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
Это векторное уравнение может быть представлено в координатной форме:
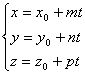
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:
![]()
Определение.
Направляющими косинусами прямой
называются направляющие косинусы
вектора ![]() ,
которые могут быть вычислены по формулам:
,
которые могут быть вычислены по формулам:
![]()
![]()
![]()
Отсюда получим: m : n : p = cosa : cosb : cosg.
Числа
m, n, p называются угловыми коэффициентами
прямой. Т.к.![]() -
ненулевой вектор, то m, n и p не могут
равняться нулю одновременно, но одно
или два из этих чисел могут равняться
нулю. В этом случае в уравнении прямой
следует приравнять нулю соответствующие
числители.
-
ненулевой вектор, то m, n и p не могут
равняться нулю одновременно, но одно
или два из этих чисел могут равняться
нулю. В этом случае в уравнении прямой
следует приравнять нулю соответствующие
числители.
