Metod_B1.V.DV.23.01_09.03.01_04.06.2016_pz

т.е в момент времени t = t3 в очереди небудет требований с вероятностью 5/16,

будет одно требование с вероятностью 1/2, и будут два требования с вероятностью 3/16.

2) После достаточно большого числа шагов система обслуживания войдёт в стационарный режим, и вероятности того, что в очереди будет 0, 1 или 2 требования, равны соответствующим компонентам вектора Ь. Вектор b есть решение уравнения b*P=b. Получаем b следующим образом:

Следовательно,

1/2 b1+ 1/2 b2 = b1*

1/2 b1 + 1/2b2+1/8b3=b2*, 3/8b2 + 7/8b3=b3*,

а также b, + b2 + b3 = 1 Разрешая систему относительно b1 ,b2, b3, получаем b = (b1, b2,b3) = (1/17, 4/17, 12/17)

После длительного функционирования системы обслуживания в очереди будет О, 1 или 2 требования с вероятностями, равными 1/17, 4/17, 12/17 соответственно

Тема 4. Вероятностные автоматы

Вначале определяем максимальные элементы в каждой строке исходной (п*п) стохастической матрицы Р Затем определяем минимальный среди п максимальных элементов Пусть А, есть простая матрица, у которой единицы стоят в точности на тех местах, где в исходной матрице Р находятся максимальные элементы строк

Определим матрицу Р' как разность P-qA,, где q есть минимаксный элемент и компонента стохастического вектора Q Матрицу Р принимаем за исходную и повторяем разложение сначала, т е вновь определяем максимальные элементы в каждой строке и т д Блок - схема разложения на простые матрицы приведена на рис 17

Количество повторений разложения на простые матрицы всегда конечно, так как в результате однократного применения алгоритма всегда обращается в нуль хотя бы один элемент исходной матрицы Р Заметим, что данный алгоритм устроен так, что вновь получаемые простые матрицы не могут повторяться И максимальное число различных простых матриц равно

Пример 3.1 Найти разложение для следующей матрицы:

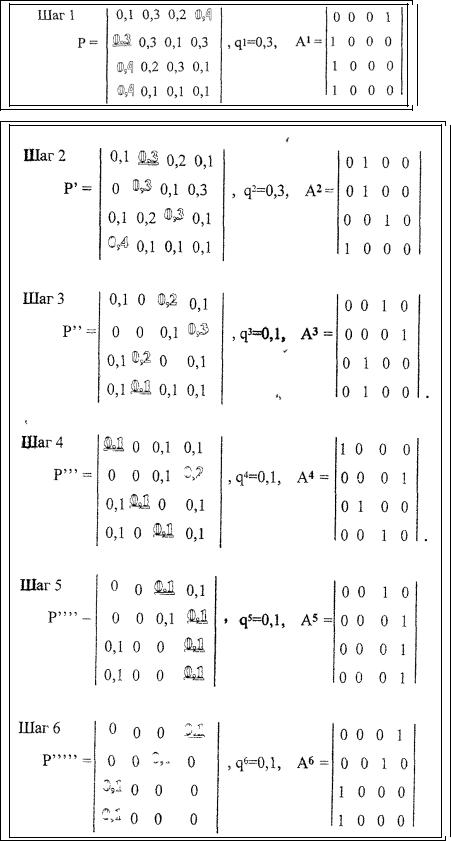
Алгоритм разложения представлен следующей последовательностью шагов Максимальные элементы в строках выделены контуром а минимаксный элемент -выделен контуром и подчеркнут

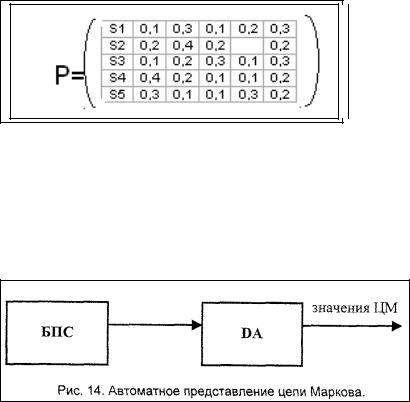
X={x1,x2,x3,x4,x5,x6}

S={S1,S2,S3,S4,S5}

Стохастическая матрица

2. Автоматный метод моделированя цепей Маркова

Автоматное представление ЦМ дано в работе [2], где показано, что простая конечная цепь Маркова может быть реализована в виде композиции детерминированного автомата (DA) и бернуллиевского потока сигналов (БПС) на входе DA (рис. 14)

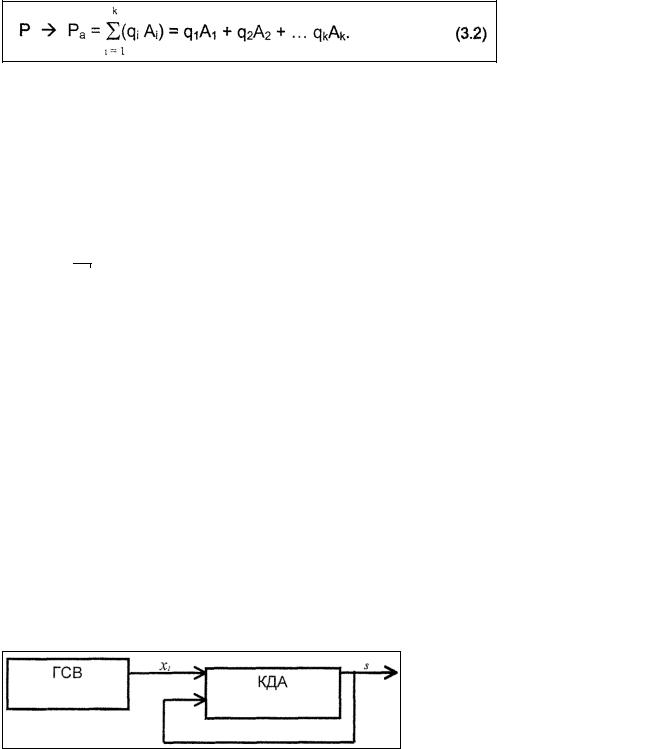
Подобный подход моделирования ЦМ можно реализовать в виде последовательности следующих двух этапов. Пусть задана стохастическая матрица Р. Преобразуем матрицу Р следующим образом:

к

Все коэффициенты q1 i=[1 ,k] в разложении (3.2) удовлетворяют условиям:

j=1

а матрицы А1, являются простыми матрицами, т.е. матрицами, элементы которых суть нули и единицы и в каждой строке матрицы есть в точности один элемент, равный единице. Набор значений (q1, q2, … , qk) будем называть имплицирующим стохастическим вектором и обозначать символом

Этап 1. Разложение стохастической матрицы в виде (3.2). Исходные данные: стохастическая матрица Р порядка nхn. Этап основан на следующей теореме:

каждая стохастическая матрица порядка n может быть представлена в виде стохастической линейной комбинации не более, чем (n-1)*n+1 простых матриц. Последовательность коэффициентов любого из таких разложений определяет стохастический вектор, имплицирующий данную стохастическую матрицу.

Этап 2. Задание детерминированного автомата, Разложение матрицы РвРд позволяет реализовать цепь Маркова, заданную матрицей Р на

основе следующей автоматной схемы:

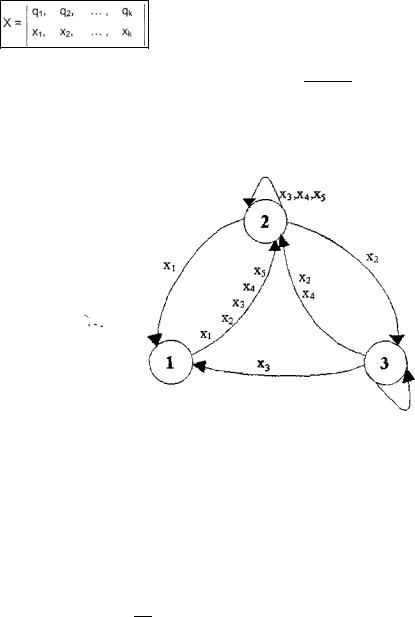
Рис. 15 Автоматная схема моделирования цепи Маркова. На рис. 15 ГСВ - генератор случайной величины X

КДА - конечный детерминированный автомат без выхода, с множеством состояний S={S1,S2,…,Sn}. На выходе ГСВ с вероятностями появляются сигналы х1 из множества

сигналов х1 , … , хk.

Сопоставим сигналу х1 подграф переходов, соответствующий матрице A1. Тогда соответствующий подграф переходов будет реализовываться с вероятностью q,. Таким образом, можно реализовать исходную матрицу переходных вероятностей

X1,X5

Рис 16 Граф - схема функционирования автомата Функционирование схемы, представленной на рис 15, иллюстрирует граф - схема на рис 16

Вершины этой граф - схемы сопоставляются состояниям автомата (вершина 1-состояние s1, вершина 2 - состояние s2 тд), а дуги - возможным переходам из состояния в состояние Дуги помечены буквами si, при поступлении которых автомат переключается в то или иное состояние с вероятностью q,

Какое состояние из s1, s2, s3 будет принято за начальное состояние s0, выбирается случайным образом, по вектору Представленная реализация ЦМ обоснована следующей теоремой

Для всякой конечной однородной цепи Маркова можно указать стационарную, с независимыми значениями входную последовательность случайных кодов и детерминированный конечный автомат без выхода, вообще говоря, со случайным начальным состоянием, такой, что данная входная случайная последовательность будет преобразовываться в заданную цепь Маркова состояний автомата

Темы 5-8. Моделирование СМО на GPSS

Пример 1. В систему массового обслуживания (Q-схему) поступает и обрабатывается фиксированное число заявок. Примем, что заявки поступают в систему по равномерному закону из интервала времени, равного от 3 до 7 мин. Обработка заявок осуществляется также по равномерному закону в интервале времени от 5 до 9 мин.

Необходимо смоделировать работу системы при поступлении и обработке 100 заявок.

Подобное условие задачи часто требуется для уточнения характера работы системы,

когда в ней обслуживание заявок осуществляется медленнее, чем поступление этих заявок в систему.

SIMULAТЕ

GENERATE 5,2,,100; Генерация 100 транзактов

SEIZE 1 ADVANCE 7,2 RELEASE 1

TERМINATE 1 Уничтожение транзактов (вывод из системы) START 100; Задание числа счетчика завершений

END

==============================================================

Пример 2. В систему массового обслуживания ( Q-схему) поступают пакеты заявок

по равномерному закону в интервале 5± 2 мин. Обработка заявок, поступивших на

первую сортировку, осуществляется также по равномерному закону в интервале 6±2

мин. Далее рассортированные заявки проходят параллельную обработку с еще одним

этапом сортировки. После обработки заявки' собираются в один пакет и выводятся из

системы. Необходимо смоделировать работу системы по обработке 100 пакетов.

SIMULA ТЕ GENERATE 5,3,,100 SPLIТ 1,CHAN1 SEIZE 1

ADVANCE 6,2 RELEASE 1 TRANSFER ,ОUТ3 СНАN1 SPLIТ 1,CHAN2 SEIZE 2

ADVANCE 6,2 RELEASE 2

TRANSFER ,ОUТ3 CHAN2 SEIZE 3 ADVANCE 6,2 RELEASE 3

OUT3 ASSEMBLE 3 TERMINATE 1 START 100

END

==============================================================

Пример 3. В систему массового обслуживания (Q-cxeмy) поступают заявки по

равномерному закону через 5 :t 2 мин. Обработка заявок осуществляется двумя

обслуживающими каналами. Поступление заявок в тот или иной канал происходит с

вероятностью 0.3 и 0.7. Обслуживание заявок каждым каналом происходит по

равномерному закону со временем 7 ±2 мин. Необходимо осуществить обработку 100

заявок при одном и двух прогонах программы.

GENERATE 5,2..100 TRANSFER 7,CHAN1,CHAN2 СНАN SEIZE 1

ADVANСЕ 7,2

RELEASE 1 TRANSFER, EXIТ CHAN7 SEIZE 2 ADVANСЕ 7,2 RELEASE 2

EXIТ TERMINATE 1 START 100

CLEAR START 100 END

============================================================

Пример 4.Блок TRANSFER в режиме BOTH. Пусть в условиях примера 3 заявки

могут обрабатываться на одном из двух приборов; на l-м за 5±3 мин, на 2-м за 7±2

мин. Причем предпочтительнее обработка на первом приборе

GENERATE 5,2,,100

TRANSFER BOTH,CHANI,CHAN2

CHANI SEIZE 1

ADVANCE 5,3'

RELEASE 1

TRANSFER ,EXIТ CHAN2 SEIZE 2 АDVANCE 7,2 RELEASE 2

EXIТ TERMINATE 1 START 100

END

=============================================================Прим

ер 5. Рассмотрим работу .блока TRANSFER в режиме ALL. В систему массового

обслуживания (Q-cxeмy) поступают заявки по равномерному закону со временем 5±2

мин. Обработка заявок происходит водном из четырех каналов обслуживания, для

которых времена обслуживания составляют: 17±2 мин, 12±2 мин, 9±2 мин и 3±2 мин

соответственно. Смоделировать работу системы по обработке 100 заявок четырьмя

каналами, когда вновь поступающая заявка обслуживается любым свободным

каналом.

SIMULAТЕ GENERATE 5,2,,100 SPLIT1,CHAN2 SPLIT1,CHAN3

TRANSFER ALL,CHANl,CHAN4,4 CHAN1 SEIZE 1

ADVANCE 17,2 RELEASE 1 TRANSFER ,EXIТ СHAN2 SEIZE 2 ADVANCE 12,2 RELEASE 2 TRANSFER, EXIT СHAN SEIZE 3 ADVANCE 9,2 RELEASE 3 TRANSFER ,EXIT СHAN4 SEIZE 4 ADVANCE3,2 RELEASE 4

EXIТ TERMINATE 1 START 100

END

============================================================