Курсовая динамичка / Курсовая динамичка

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное учреждение высшего образования

Российский государственный гидрометеорологический университет (РГГМУ)

Кафедра ДАКЗ

Курсовая работа на тему: « Расчёт характеристик в стационарном горизонтально-однородном ППС»

Вариант № 5

Выполнил: ст. гр. ПМ-Б15-1-3

Скачков И.В.

Проверила: доц. кафедры ДАКЗ

Еремина Н.С.

Санкт-Петербург 2017

Содержание:

1. Планетарный пограничный слой атмосферы. Модель Экмана.................................3

2. Постановка задачи..........................................................................................................4

3. Расчеты ...........................................................................................................................4

4. Графический материал ..................................................................................................6

График – Спираль Экмана;

График зависимости силы трения, силы Кориолиса и силы барического градиента от высоты;

Графики баланса сил на уровнях 0,2Н; 0,5Н; 0,8Н.

5. Вывод ..............................................................................................................................8

1.Планетарный пограничный слой атмосферы. Модель Экмана.

ППС-это нижний, начинающийся от земной поверхности слой атмосферы (тропосферы), свойства которого в основном определяются динамическими и термическими воздействиями этой поверхности. Толщина слоя от 300—400 до 1500—2000 м, в среднем около 1000 м. Она тем больше, чем больше шероховатость земной поверхности и чем интенсивнее развитие турбулентности, а потому увеличивается с усилением ветра и с уменьшением устойчивости стратификации. Вследствие уменьшения с высотой турбулентного трения скорость ветра в ППС возрастает с высотой, приближаясь к скорости градиентного ветра на верхней границе ППС (на уровне трения). Угол отклонения ветра от изобар при этом приближается к нулю. В нижней части ППС (в приземном слое) скорость ветра растет с высотой приблизительно по логарифмическому закону (пропорционально логарифму высоты), в вышележащей части ППС (в слое Экмана) изменение скорости и направления ветра приближенно описывается спиралью Экмана. Для ППС характерна повышенная концентрация аэрозолей (пыли, дыма, тумана).

Свойствами планетарного пограничного слоя в значительной мере определяются вертикальные турбулентные потоки тепла, влаги и количества движения а также локальные вертикальные упорядоченные токи (конвективные явления, орографические эффекты) благодаря которым и осуществляется динамическое и термическое взаимодействие атмосферы с подстилающей поверхностью.

Спираль Экмана – это математическое представление распределения ветра с высотой в пограничном слое атмосферы при допущении, что коэффициент турбулентности k в этом слое не меняется с высотой, движение горизонтальное и установившееся, изобары прямолинейны и параллельны и геострофический ветер не меняется с высотой.

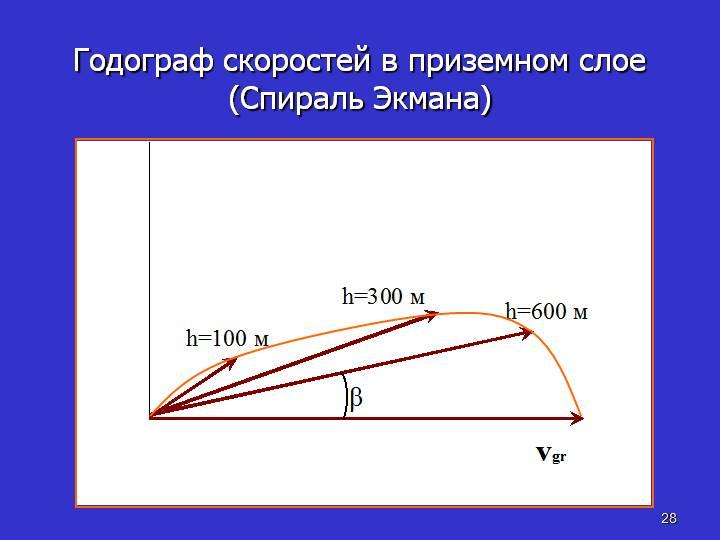
Интегральная модель планетарного пограничного слоя

При стационарности и горизонтально-однородности системы уравнения движения принимают следующий вид:

(1)

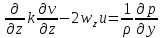(2)

Предполагая градиент давления внешним параметром и выражая его через геострофический ветер, то уравнения (1) и (2) примут вид:

(3)

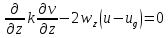(4)

Также систему (1) и (2) можно переписать в векторной форме:

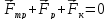(5)

Уравнения неразрывности имеет вид:

(6)

Для замыкания системы используем уравнение баланса энергии турбулентности:

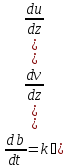(7)

Предположим, что все характеристики турбулентности можно представить, как функции от характерного размера турбулентных пульсаций – масштаба турбулентности l – и кинетической энергии турбулентности b

С помощью π-теоремы получили выражения для коэффициента турбулентности k и диссипации ε:

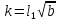(8)

где

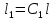
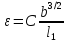(9)

где

С=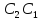

Для определения 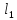воспользуемся выражением, обобщающим формулу Кармана на случай двумерного стратифицированного потока:

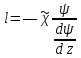(10)

где

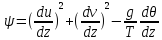
Уравнение притока тепла в общем виде:

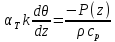(11)

где

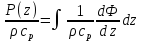
а 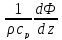– сумма радиационного баланса и фазового притока тепла

Аналогично уравнение притока влаги:

(12)

где

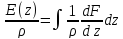
а 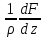– фазовый приток влаги.

Запишем системы уравнений (1-7), (11-12) и граничных условий для простейшего случая априорного профиля k.

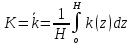(13)

где H – высота планетарного пограничного слоя

Уравнения движения согласно (1) и (2) уравнению примут вид:

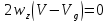+ (14)

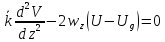(15)

Также уравнения притоки тепла и водяного пара записываются в предположении о линейном убывании их вертикальных турбулентных потоков до 0 к верхней границе ППС.

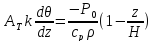(16)

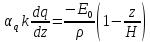(17)

Уравнение неразрывности сохраняет свой исходный вид.

Для определения среднего коэффициента турбулентности 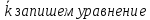, по аналогии похожим на формулу 8, но она ещё будет зависеть от средней удельной кинетической энергии турбулентности и всей высоты пограничного слоя.

(18)

Модель экмановского пограничного слоя

Годограф ветра, описываемый соотношениями (17) и (18), называется спиралью Экмана. Для частного случая, когда ось ox совпадает с направлением геострофического ветра (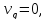 , формулы (17) и (18) примут вид:

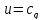(1- (19)

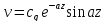(20)

На рис. 1 из практического раздела показан универсальный годограф ветра, построенный в системе координат 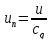и 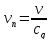; точки на кривой, соответствуют разным значениям 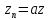. Вектор ветра на высоте 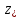равен вектору, имеющему начало в точке 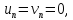а конец в точке с соответствующим значением 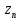. В пограничном слое, как следует из рис. 1, имеет место правое вращение ветра с высотой.

Проанализировав уравнения (17-20) видны влияние турбулентности на вертикальный профиль ветра: сильная турбулентность (большие значения 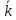) вызывает медленное увеличение ветра с высотой, а слабая — быстрое. Зная выражение (φ — широта), то увеличение широты соответствует уменьшению коэффициента турбулентности, а уменьшение 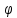— увеличению .

Угол между вектором геострофического ветра и вектором вектора на любой высоте определяется как

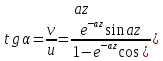(21)

4. Условие задачи.

I.На десяти рабочих уровнях с шагом 0,1H определить:

1)Составляющие, модуль и направление вектора скорости ветра.

2)Составляющие, модуль и напрвление сил барического градиента, Кориолиса и трения

II.Построить

1)спираль Экмана

2)Вертикальные профили сил

3)Баланс сил на уровнях 0,2H; 0,5H ; 0,8H.

III.Проанализировать полученные результаты.

Коэффициент турбулентности рассчитать по формуле, полученной на основании уравнения баланса удельной кинетической энергии турбулентности, приняв m=10^(-5).

Считать, что на верхней границе ППС ветер впервые совпадает с геострофическим ветром по направлению. Принять:dp/dy=-1,3 Гпа\100км, P0=-0,05 кал/(см^2мин), широта места φ=55˚; p=1,3кг/м^3; Т=273 К.

5.Рассчеты.

z	U	V	C	tg (α)	α	Fkx	Fky	Fk
111,406	2,55	1,89	3,18	0,7392	36,475321	0,0002257271	-0,0003053	0,000379795
222,811	4,75	2,627	5,436	0,5518	28,892015	0,0003137488	-0,0005683	0,00064923
334,217	6,45	2,639	6,974	0,4090	22,248775	0,0003151820	-0,0007709	0,00083292
445,622	7,63	2,266	7,966	0,2969	16,540549	0,0002706337	-0,0009121	0,00095139
557,028	8,37	1,741	8,552	0,2080	11,754354	0,0002079317	-0,0010000	0,00102138
668,433	8,76	1,209	8,849	0,1381	7,8639171	0,0001443937	-0,0010469	0,00105685
779,839	8,91	0,751	8,951	0,0843	4,8240316	0,0000896937	-0,0010652	0,00106903
891,244	8,92	0,399	8,931	0,0448	2,5661833	0,0000476535	-0,0010655	0,00106665
1002,65	8,84	0,153	8,845	0,0174	0,9973769	0,0000182731	-0,0010562	0,00105637
1114,05	8,73	0	8,735	0	0,0037857	0	-0,0010432	0,00104324

Fтр(х)	Fтр(у)	Fтр	β=-(90-α)	tgY	Y	Y= +-(180-Y)
-0,00022572717	-0,00069461143	0,000730368	-53,524679	3,07935	72,0091252	-107,990875
-0,00031374883	-0,00043162136	0,000533606	-61,107985	1,3773	54,0182505	-125,98175
-0,0003151820	-0,00022906406	0,000389628	-67,751224	0,72727	36,0273757	-143,972624
-0,00027063374	-0,00008789500	0,000284549	-73,459451	0,32562	18,0365009	-161,963499
-0,00020793175	0,00000000721	0,000207931	-78,245645	0,0008	0,04562616	-179,954374
-0,00014439373	0,00004694413	0,000151833	-82,136083	0,32386	17,9452486	162,0547514
-0,00008969370	0,00006521729	0,000110897	-85,175968	0,72484	35,9361234	144,0638766
-0,00004765351	0,00006557558	0,000081061	-87,433817	1,3727	53,9269981	126,0730019
-0,00001827315	0,000056259863	0,000059153	-89,002623	3,06274	71,9178729	108,0821271
0,000000000000	0,000043241735	0,0000432417	-89,996214	627,882	89,9087477	90,09125233

sinϕ=	0,82
ι=	1,19^-4
Po=	70
Cg	9,02
k	13,62
a	0,0021
H	1499,40

График – Спираль Экмана.

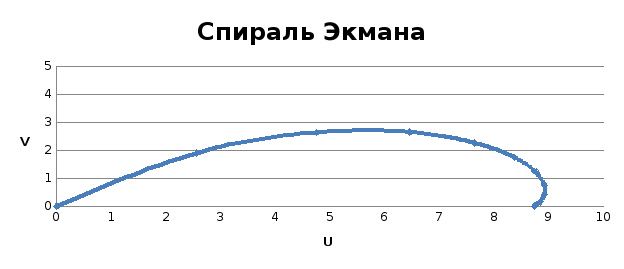
График зависимости силы трения, силы Кориолиса и силы барического градиента от высоты

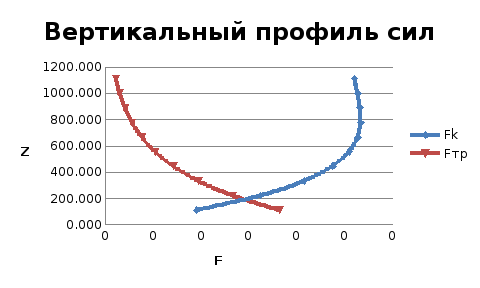
В) Графики баланса сил на уровнях 0,2Н; 0,5Н; 0,8Н.

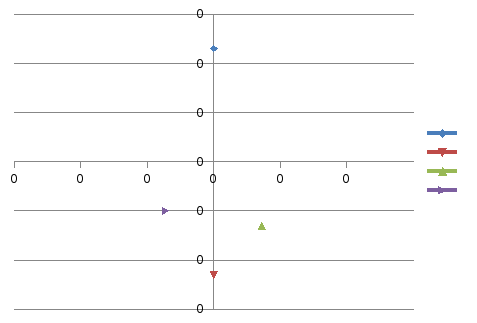
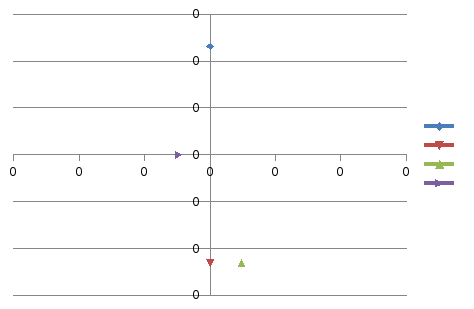
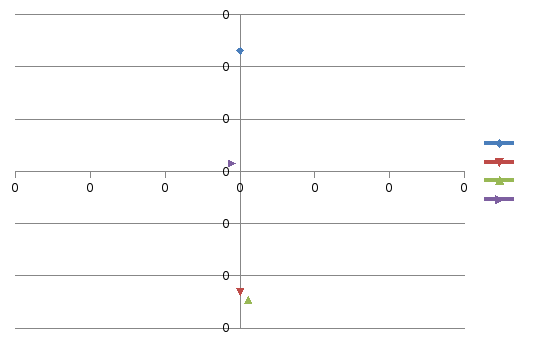
7.Вывод.

В рамках данной модели, изобары направлены вдоль оси Х, поэтому составляющая скорости геострафического ветра Vg=0, и, следовательно, составляющая Ug=|Cg| и направлена вдоль этой оси. Исходя из этого условия, составляющая силы барического градиента Fpx=0, и, следовательно, |Fp|=Fpy. Fp направлена вверх, под углом 90 градусов от оси Х, и не меняет свое значение на протяжении всего слоя. Составляющая скорости реального ветра V уменьшается с высотой, а U увеличивается. На верхней границе ППС реальный ветер по направлению совпадает с геострафическим ветром Cg. Сила Кориолиса Fk направлена под углом 90 градусов от направления движения вправо в северном полушарии и с высотой ее значение возрастает. На верхней границе ППС направление Fk становится равным -90 градусов, что говорит о том, что она становится равнозначной силе барического градиента Fp и они уравновешивают друг друга. Сила трения Ftr у земли имеет максимальное значение, и чем ближе к верхней границе ППС, тем ее значение становится меньше.