12. Непрерывные случайные величины. Функция плотности вероятности, ее свойства.
Непрерывной случайной величиной называется случайная величина, все возможные значения которой целиком заполняют некоторый промежуток на числовой прямой.
Плотностью распределения вероятностей непрерывной, случайной величины Х называют функцию f(x) - первую производную от функции распределения F(x):
f(x) = F (x),
т.е. функция распределения является первообразной для плотности распределения.
Свойства плотности распределения
1) Плотность распределения неотрицательная функция: f(x) 0.
2) Несобственный интеграл от плотности распределения в пределах от -? до +? равен единице:
3) Если все возможные значения случайной величины принадлежат интервалу (a, b), то
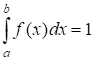
Функция f(x) определяет плотность распределения вероятности для каждой точки Х, аналогично плотности массы в точки.
13.Числовые характеристики непрерывной случайной величины.
К основным числовым характеристикам непрерывной случайной величины относятся мода, медиана, математическое ожидание, дисперсия и среднеквадратическое отклонение.
Модой непрерывной случайной величины X называется такое ее значение, при котором плотность вероятности максимальная. Случайная величина может иметь несколько мод.
Обозначается мода М или Мо. С геометрической точки зрения мода – значение аргумента x, при котором график функции плотности распределения принимает максимальное значение.
Нахождение моды - известная задача дифференциального исчисления поиска экстремума на множестве. Если функция f(x)дифференцируема на интервале, то ищутся “подозрительные” на локальный экстремум точки {x0i}, а из них выбирается max f(x0i), который нужно сравнить со значениями f(x) на границах интервала.
Медианой Me непрерывной случайной величины x называется такое ее значение m, для которого равновероятно, что случайная величина x больше или меньше m:
P(X<m)=P(X>m)=1/2.
В случае, когда ось симметрии кривой распределения y=f(x) совпадает с прямой x=m, то выполняется соотношение равной вероятности для x=m в точке m, и тогда Me=m=m.
В общем случае медиана есть корень алгебраического уравнения F(x)=1/2 или интегрального уравнения
.
С геометрической точки зрения медиана делит площадь под графиком функции плотности вероятности на две равные части.
Математическим ожиданием непрерывной случайной величины называется интеграл
.
Для функции от НСВ справедливо утверждение, что она распределена так же, как и сама НСВ. Поэтому математическим ожиданием функции G от НСВ X называется интеграл
.
С геометрической точки зрения математическое ожидание случайной величины равно абсциссе центра тяжести площади, ограниченной кривой распределения и осью абсцисс. В рассматриваемом случае, когда кривая распределения симметрична относительно прямой x=m, математическое ожидание также совпадает с этой абсциссой. Тогда математическое ожидание, мода и медиана равны между собой:
m=М(X)=Me=m.
Дисперсиянепрерывной случайной величины X находится по формуле
.
Дисперсия характеризует степень рассеяния значений случайной величины от своего среднего значения. Все свойства математического ожидания и дисперсии, сформулированные для ДСВ, сохраняются и для НСВ. Как и для ДСВ, формула дисперсии имеет и другой вид:
