Постановка задачи

Дифференциалы этих постоянных аддитивных величин кинетических энергий (2) и (3) равны нулю:

• для первого цилиндрического тела:

• для второго цилиндрического тела:

Согласно теореме о механической энергии замкнутой системы, энергия не появляется и не исчезает, а переходит из одного вида в другой, поэтому дифференциалы кинетических энергий (4) и (5) двух взаимодействующих тел всегда равны друг другу, поскольку дифференциалы кинетических энергий систем материальных точек равны элементарным работам всех сил, приложенных к их точкам, и ввиду того, что приложенные к системам материальных точек силы равны друг другу по величине:

1 1 1 + 1 1 1 + 1 1 1 + 1 1 1 = = 2 2 2 + 2 2 2 + 2 2 2 + 2 2 2 (6)

3. Взаимодействие центра масс одного тела и с центром масс второго тела

Содержание

А теперь рассмотрим движение двух идентичных тел, взаимодействующих друг с другом центрами масс (центральное взаимодействие).

Согласно закону сохранения механической энергии и с учётом особенностей участия первого и второго тела одновременно только в поступательном движении, баланс дифференциалов кинетических энергий приобретает вид:

При постоянных ускорениях поступательного движений, когда дифференциалы = 0 равны нулю, баланс дифференциалов кинетических энергий тел принимает вид:

Ньютон обозвал коэффициент пропорциональности, связывающий произведения масс взаимодействующих тел на их ускорения, силой. Если сохранить такой же подход, как и Ньютон, то из (9) следует, что силой (коэффициентом пропорциональности) является произведение массы тела на квадрат его ускорения поступательного движения:

Из чего следует, что постулированные Ньютоном второй и третий законы не соответствует тем результатам, которые получены из закона сохранения энергии, а поскольку в основе закона сохранения импульсов тоже лежат законы Ньютона, то, следовательно, и они не являются следствием закона сохранения энергии, это будет рассмотрено и доказано дополнительно.

Вопрос о том, какой из этих законов справедлив − отдельный, но если всё же закон сохранения энергии справедлив, то второй закон Ньютона должен бы был иметь вид, соответствующий (10).

Из (10) прямо следует, что сила не может являться вектором.

Одно из объяснений разногласий полученного результата с постулированными Ньютоном законами состоит в том, что законы Ньютона постулировались, исходя из их применимости исключительно только в инерциальных системах отсчёта, предполагающих субъективность анализа процессов, даже несмотря

2

на то, что объективно физически непосредственно сами величины энергий тел не могут зависеть от того, в какой инерциальной системы отсчёта рассматриваются и анализируются состояния этих тел, поскольку это противоречило бы самой логике закона сохранения энергии.

Другое из объяснений состоит в том, что постулированная Ньютоном сила характеризует её действие не на всё тело, а только лишь на одну его точку в предположении, что тело является абсолютно твёрдым и вся его масса сосредоточена именно в этой точке, исключая, тем самым, распределение сил взаимодействия по всему объёму или по всей поверхности тела, что также противоречит логике здравого смысла, поскольку согласно лемме о параллельном переносе сил такая точка приложения силы может находиться не только в центре масс, но и в совсем другой точке, называемой мгновенным центром вращения масс этого же тела, что не придаёт порядка этим законам и выглядит неряшливо, если так можно выразиться применительно к законам.

4. Взаимодействие тел при их исключительно вращательных движениях

Содержание

Рассмотрим теперь замкнутую систему, состоящую из соосно взаимодействующих тел, когда каждое их них способно участвовать только исключительно во вращательных движениях.

Согласно закону сохранения механической энергии и с учётом указанных особенностей участия тел только во вращательных движениях, баланс (6) дифференциалов кинетических энергий приобретает вид:

Равенство (13) указывает на то, что в нём коэффициентом пропорциональности является момент,

5. Взаимодействие центра масс одного тела и с поверхностью вращения второго тел

Содержание

Рассмотрим результаты опытного исследования движения на плоскости двух идентичных транспортных контейнеров (рис. 1) с размещёнными внутри них цилиндрическими телами равных масс (масса контейнера на два порядка меньше массы тела), которые через отверстия в контейнерах взаимодействуют друг с другом посредством гибкой малорастяжимой тяги таким образом, что одна и та же по величине сила взаимодействия приложена к центру масс первого тела и к поверхности вращения второго тела, в результате чего к первому телу приложена только сила, а ко второму телу — приложен момент этой же силы.

3

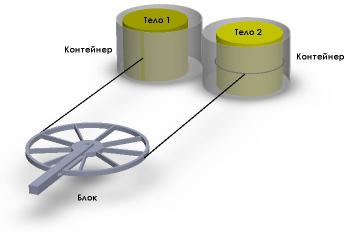
Рис. 1

Согласно лемме о параллельном переносе сил и теореме Пуансо, действие момента силы, направление которой не проходит через центр масс второго тела, аналогично одновременному действию момента пары сил и силы, приложенной к мгновенному центру вращения тела, а поскольку момент пары сил по своей природе не имеет равнодействующей, то, помимо действия приложенной к центру масс первого тела уравновешенной силы со стороны мгновенного центра вращения второго тела, к нему прикладывается ещё и неуравновешенная моментом пары антипараллельных сил та сила, под действием которой оно приобретает дополнительное ускорение поступательного движения, в результате чего результирующая величина ускорения поступательного движения первого тела всегда превышает величину ускорения поступательного движения второго тела, что и подтверждается представленными далее результатами расчётов и видеоматериалами результатов проведения реальных опытов.

Согласно закону сохранения механической энергии и с учётом указанных особенностей участия первого тела только в поступательном движении и участия второго тела одновременно в поступательном и вращательном движении, баланс (6) дифференциалов кинетических энергий приобретает вид:

стеме не равна нулю, когда направление действия силы их взаимодействия не проходит через центр

В соответствии с правилами дифференцирования, в (20) знаки ускорений (производных) указывают не их направления, а на их возрастание — при знаке (+) или убывание — при знаке (–).

4