- •Противоречия
- •Особенность законов Ньютона и законов сохранения импульсов и моментов импульсов
- •Взаимодействия тел в замкнутых системах согласно закону сохранения энергии
- •Опытное подтверждение представленных доказательств
- •Конструктивное исполнение транспортных систем
- •Скорости, ускорения и полная кинетическая энергия замкнутой системы

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
© Юрьев Н. Я. апрель, 2017 г.
Содержание
1 |
Противоречия |
1 |
2 |
Особенность законов Ньютона и законов сохранения импульсов и моментов импульсов |
2 |
3 |
Взаимодействия тел в замкнутых системах согласно закону сохранения энергии |
4 |
4 |
Опытное подтверждение представленных доказательств |
9 |
5 |
Конструктивное исполнение транспортных систем |
11 |
6 |
Скорости, ускорения и полная кинетическая энергия замкнутой системы |
14 |
1. Противоречия
Содержание
До сих пор, и не только в среде обывателей, существуют взаимоисключающие взгляды на возможность реализации замкнутых электромеханических систем, способных приобретать ускорения без их взаимодействия с массами внешней среды в качестве опоры только лишь за счёт преобразования внутренней энергии встроенных её источников, например, электрических аккумуляторов.
Многовековое состязание научных течений в механике привело к тому, что, с одной стороны, сформировалось отрицание такой возможности, основанное на безуспешных попытках повсюду применять законы Ньютона, основанные на представлениях 400 летней давности о никогда несуществовавших в природе инерциальных системах отсчёта, не способных испытывать ускорения1, а с другой стороны были представлены научные теоретические и практические обоснования такой возможности, основанные на современных положениях теоретической механики2 и на законах сохранения энергии3, подтверждённых многочисленными опытами.
Единый же для этих научных течений математический аппарат указывает на то, что ничего не меняется в результате исключения из пользования систем отсчёта с направляющими в пространстве координатными осями, не способными испытывать ускорения, поскольку при абсолютном дифференцировании знаки производных функций характеризуют не направления их изменения, а только исключительно их увеличение или уменьшение, делая системы отсчёта совершенно излишними и даже непригодными для исследования динамики пространственных процессов.
Если бы Ньютон писал свои законы не в кабинете, а в карете, и связал бы начало отсчёта с кучером, то он, возможно, смог бы написать и такие свои законы, из которых бы следовало, что при движении кареты любые тела могут самопроизвольно приходить в движение без какого либо внешнего воздействия,
апри отсутствии движения кареты эти же самые тела не могут самопроизвольно перемещаться.
1«Современная механика основывается на ряде закономерностей, установленных в форме, независимой от коор-
динатных систем, применяемых при получении и исследовании упомянутых закономерностей. Такая форма называется инвариантной. Математическим аппаратом, который позволяет находить основные соотношения механики в инвариантной форме, является тензорное, или абсолютное дифференциальное исчисление.» [Кильчевский Н. А. Курс теоретической механики. Том 1. (Кинематика, статика, динамика точки). М., 1972, 456 стр. с илл. (стр. 25)]
2Однако отсюда вовсе не следует, что внутренние силы не влияют на движение системы. Это было бы так, если
внутренние силы были бы уравновешенной системой сил. Однако они таковой не являются, поскольку приложены к разным точкам. Если система состоит из нескольких твёрдых тел, то работа внутренних сил каждого твёрдого тела равна нулю, но работы внутренних сил, действующих между каждыми двумя твёрдыми телами, принадлежащими к этой системе, в общем случае не равны нулю [Кильчевский Н. А. Курс теоретической механики. Том 1. (Кинематика, статика, динамика точки). М., 1972, 456 стр. с илл. (стр. 147)]
3. . . , которые не зависят от характера действующих сил и поэтому с их помощью можно получить ряд важных сведений о поведении механических систем даже в тех случаях, когда силы оказываются неизвестными. [Курс общей физики. В 5 кн. Кн. 1. Механика: Учеб. пособие для втузов/ И. В. Савельев. — М.: ООО «Издательство Астрель»: ООО
«Издательство АСТ», 2002. — 336 с.: ил. (стр. 84)]

В основе предоставленных здесь теоретических доказательств лежат практические подтверждённые обоснования того, что при определённых способах организации взаимодействия тел их общий центр масс способен приобретать любое, наперёд заданное ускорение поступательного движения без всякого взаимодействия с массами внешней среды в качестве опоры, причём эти доказательства совершенно ни в чём не противоречит всем известным законам при их верном толковании, поскольку основаны исключительно только на общеизвестных положениях, многократно излагаемых уже около сотни лет почти во всех учебных курсах физики и теоретической механики.
2. Особенность законов Ньютона и законов сохранения импульсов и моментов импульсов
Содержание
На законы Ньютона ссылаются оппоненты, когда пытаются обосновывать и обобщать утверждения о том, что замкнутая система не способна приобретать ускорения без взаимодействия с массами внешней среды в качестве опоры, возможно, забывая о том, что в основу первого закона Ньютона положено всего лишь его личное и специально оговорённое в первом законе предположение о возможности существовании таких инерциальных систем отсчёта, в которых эти законы могут выполняться, хотя на самом деле реально в природе не существуют подобные инерциальные системы отсчёта, не способные испытывать ускорения, и только поэтому сами законы Ньютона в основе своей не являются фундаментальными и из-за наличия ограничений, накладываемых использованием инерциальных систем отсчёта, имеют весьма ограниченное и всего лишь частное применение.
Инерциальные системы отсчёта, реально не существующие в природе, уже изначально предполагают их пребывание в стационарном состоянии при полном отсутствии ускорений, а из этого естественно сразу же следует то, что какое бы тело не взаимодействовало бы с другим иным телом в такой неподвижной инерциальной системой отсчёта, общий центр их масс никогда не будет способен приобретать ускорение поступательного движения, поскольку одно их тел заведомо принято в качестве неподвижного и жёстко связанного с неподвижной инерциальной системой отсчёта.
Особенность законов Ньютона как раз и состоит в том, что их действие распространяется только исключительно на точки виртуальных абсолютно твёрдых тел, принадлежащих таким же несуществующим виртуальным неподвижным инерциальным системам отсчёта, а не к любым реальным деформируемым телам вне систем отсчёта координат, обладающих помимо массы ещё и моментом инерции, что предполагает рассмотрение движения не самих тел, а только лишь движение точек, одна из которых заведомо принята в качестве неподвижной, но к которой сила всё же приложена по отношению другой точки, в которой, якобы, может быть сосредоточена вся масса исследуемого подвижного тела, но без наличия и последующего учёта её момента инерции, поскольку тачка не способна характеризоваться размерами.
Поэтому, когда центр масс тела не расположен на направлении действия силы, то законами Ньютона невозможно пользоваться, а законы сохранения импульсов и моментов импульсов, вытекающие из законов Ньютона, описывают всего лишь частные производные инвариантных к системам отсчёта координат функций кинетических энергий тел по всего лишь частным скоростям поступательного или вращательного их движения, причём, согласно теореме Кёнига и закону сохранения энергии, сами такие функции кинетических энергий определяются суммами постоянных аддитивных и неопределённых величин вне всяких систем отсчёта координат:
|
|
2 |
|
|
2 |
|
|
2 |
|
2 |
|
|
|
2 |
|
2 |
|
|
= |
2 |
|
+ |
2 |
= |
|
2 |
|
|
+ |
|
|
2 |
|
|
= |
(1) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Именно только частные производные функции (1) кинетической энергии по частным же скоростям или только лишь поступательного , или только лишь вращательного их движения как раз и являются тем, что именуется в физике и теоретической механике соответственно импульсами и моментами импульсов тел:
∂ |
|
= |
(2) |
|
|
∂ |
|||
|
∂ |
= |
(3) |
|
|
∂ |
|||
2
С точки зрения математики естественно, что всего лишь только частные производные функций кинетических энергий должны существенно отличаться от их же полных производных и не должны быть способны в полном объёме отражать совокупные свойства тел в динамике, поскольку обладание телами только лишь импульсами или только лишь моментами импульсов в общем случае не есть то же самое, что и одновременное обладание этими же телами величинами кинетических энергий поступательного и вращательного движения, что и объясняет появление взаимоисключающих противоречий между результатами, получаемыми с использованием закона сохранения энергии, и теми результатами, которые основаны на использовании законов Ньютона, лежащих в основе закона сохранения импульсов и моментов импульсов.
Апоскольку законы Ньютона являются всего лишь частными законами, то на их основе зачастую
иделается ошибочный вывод о том, что работа сил и моментов внутри замкнутой многомассовой изменяемой системы равна нулю, а сама область применения закона сохранения импульсов и моментов импульсов ограничивается только лишь неизменяемыми абсолютно твёрдыми телами, которые в природе не существуют, а то, что законы Ньютона доказывают, что, например, утюг или гиря не способны самостоятельно приобретать ускорения без действия на них внешних сил, помимо того, что это
итак очевидно, вовсе не являться доказательством того, что работа внутренних сил в многомассовых изменяемых замкнутых системах обязательно должна быть равна нулю, а также не являться доказательством и того, что массы и моменты инерции таких замкнутых систем не могут приобретать ускорения без взаимодействия с массами внешней среды в качестве опоры.
В учебных курсах теоретической механики существо этих отличительных особенностей неизменяемых и изменяемых замкнутых систем применительно к законам сохранения импульсов и моментов импульсов раскрывается, например, следующим образом:
•Работа внутренних сил в изменяемой системе в общем случае не равна нулю [М. И. Бать, Г. Ю. Джанелидзе, А. С. Кельзон. Теоретическая механика в примерах и задачах. т. II (динамика) - М., 1975 г., 608 стр. с илл. (стр. 305)];
•В то время как главный вектор и главный момент равны нулю, сумма работ внутренних сил, вообще говоря, нулю не равна [Теоретическая механика. Учеб. для вузов/Н. Н. Поляхов, С. А. Зегжда, М. П. Юшков; Под ред. П. Е. Товстика. Н. Н. - 2-е изд., перераб. и доп. - М.: Высш. шк., 2000. - 592 с.: илл. (стр. 147)];
•В законах количеств движения и кинетических моментов внутренние силы не фигурировали, ибо их главный вектор и главный векторный момент относительно любого центра
равны нулю; но алгебраическая сумма работ внутренних сил в общем случае материальной системы не равна нулю, как показано в п. 5° § 2, она равна нулю в частном случае абсолютно твёрдого тела, но уже для упругого тела не равна нулю [Геронимус Я. Л. Теоретическая механика. Очерки об основных положениях. М., 1973 г. 512 стр. с илл. (стр. 206)];
•Доказательство проведено для двух точек абсолютно твёрдого тела, за которые мы можем принять любые точки тела, а потому оно относится ко всем точкам твёрдого тела. В случае упругого тела или изменяемой системы точек сумма работ внутренних сил не равна нулю. Так, например, при падении камня на Землю силы взаимодействия между камнем и Землёй (внутренние силы системы Земля — камень) равны и противоположны, но сумма работ этих сил не равна нулю [Гернет М. М. Курс теоретической механики. Изд. 3-е, перераб. и доп. Учебник для вузов. М., «Высшая школа», 1973. 464 с. с илл. (стр. 374)];
•Как уже известно, главный вектор и главный момент всех внутренних сил для любой механической системы равны нулю. Сумма работ внутренних сил равна нулю только в случае твёрдого тела, а для любой механической системы в общем случае она не равна нулю [Добронравов В. В., Никитин Н. Н., Дворников А. Л. Курс теоретической механики. Изд. 3-е, перераб. Учебник для вузов. М., «Высшая школа». 528 с. с илл. (cтр. 293)];
•При виртуальном перемещении твёрдое тело остаётся твёрдым. Но ничто не запрещает нам рассматривать перемещения деформируемых тел. Следует только помнить, что в этом случае работа внутренних сил не будет равна нулю [Парс Л. А. Аналитическая динамика. М., 1971. 636 стр. с илл. (стр. 38)].
3
•Итак, мы доказал теорему об изменении кинетической энергии: дифференциал кинетической энергии системы материальных точек равен элементарной работе всех сил, приложенных к её точкам.
В формулировке этой теоремы весьма существенно, что в ней речь идёт о всех силах, а не только о внешних силах, как это имело мест в предыдущих теоремах этой главы. В предыдущих теоремах суммировались сами силы или их моменты и в силу третьего закона Ньютона сумма всех внутренних сил (или их моментов) оказывалась равной нулю и могла
быть отброшена. Теперь же в теореме об изменении кинетической энергии суммируются скалярные произведения , и даже если силы и +1 равны, действуют вдоль одной прямой и направлены противоположно, сумма + +1 +1 может быть (и часто бывает)
отлична от нуля, так как в общем случае
= +1.
Рассмотрим теперь систему, которая не является консервативной, но у которой часть сил потенциальна. Для такой системы
= + ,
где — элементарна работ непотенциальных сил, и
( − ) =
или
= .
Следовательно, дифференциал полной энергии для систем, на которые действуют непотенциальные силы, равен элементарной работе не потенциальных сил.
Таким образом, кинетическая энергия при движении замкнутых систем не остаётся постоянной, а меняется за счёт работы внутренних сил. Эта работа равна нулю, если все силы потенциальны и движение начинается и заканчивается на одной и той же поверхности уровня = . Именно такая ситуация и имеет место в случае временных´ взаимодействий, о которых шла речь в гл. II. В иных случая скалярная мер не сохраняется неизменной даже для замкнуты систем, у которых всегда имеет место сохранение векторной меры . Суще-
ствует, однако, другая скалярная функция от координат и скоростей точек — полная энергия системы, которая остаётся постоянной при движении систем некоторого класса. Таким классом оказались все консервативные системы. Класс замкнутых и класс консервативных систем не совпадают, а пересекаются, так как замкнутые системы могут быть консервативными и неконсервативными, а консервативные системы не обязательно замкнуты.» [М. А. Айзерман. Классическая механика. Издание второе, переработанное. Москва «Наука», Главная редакция физико-математической науки, 1980. (стр. 75 и 76)];
•Однако отсюда вовсе не следует, что внутренние силы не влияют на движение системы. Это было бы так, если внутренние силы были бы уравновешенной системой сил. Однако они таковой не являются, поскольку приложены к разным точкам. Если система состоит из нескольких твёрдых тел, то работа внутренних сил каждого твёрдого тела равна нулю, но работы внутренних сил, действующих между каждыми двумя твёрдыми телами, принадлежащими к этой системе, в общем случае не равны нулю [Кильчевский Н. А. Курс теоретической механики. Том 1. (Кинематика, статика, динамика точки). М., 1972, 456 стр. с илл. (стр. 147)].
3. Взаимодействия тел в замкнутых системах согласно закону сохранения энергии
Содержание
4
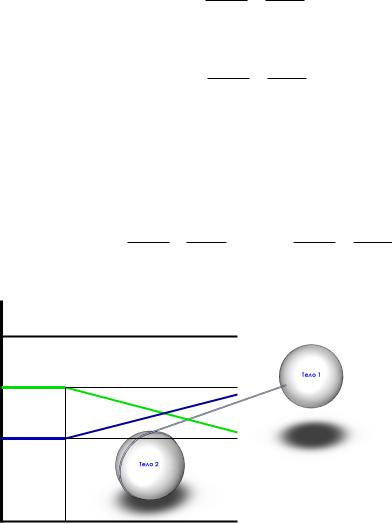
Рассмотрим изменение состояния двух взаимодействующих с равными силами идентичных по массе, |
||||||||||||||||||||||||||||||||||
форме и размерам тел, Тела 1 и Тела 2, в стационарном поле потенциальных сил, как показано на |
||||||||||||||||||||||||||||||||||
рис. 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
До момента 1 начала их взаимодействия постоянная аддитивная величина энергии каждого из |
||||||||||||||||||||||||||||||||||
них определяется суммой потенциальных и кинетических энергий, последние из которых представим в |
||||||||||||||||||||||||||||||||||
полном соответствии с теоремой Кёнига: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
• для первого тела: |
|
|
|
|
|
|
|
|
|
|
|
|
|
= 12 12 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
• для второго тела: |
Σ1 |
= 1 |
+ 1 |
+ 1 |
+ 1 |
|
2 12 |
+ 1 = ; |
(4) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= 22 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Σ2 |
= 2 |
+ 2 |
+ 2 |
+ 2 |
2 22 |
+ 2 |
= |
(5) |
|||||||||||||||||||
Когда центр масс Тела 1 начинает взаимодействовать с поверхностью вращения Тела 2, то оба тела |
||||||||||||||||||||||||||||||||||
образуют замкнутую систему, в которой, в соответствии с законом сохранения энергии, вся суммар- |
||||||||||||||||||||||||||||||||||
ная величина кинетических и потенциальных энергий, входящих в её состав тел, остаётся величиной |
||||||||||||||||||||||||||||||||||
постоянной: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Σ |
|
|
1 |
|
|
1 |
|
1 |
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= |
|
|
+ |
|
|
+ |
|
|
+ |
|
|
+ |
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
2 |
2 |
|
|
2 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
= |
1+ |
+ |
=1 |
+ 1 |
+ |
|
2 |
+ |
|
2 |
+ 2 = |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
(6) |
||||||||
|
|
|
|
|
|
|
Σ = 1 + 2 + 1 + 2 |
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0 |
|
1 |
|
+ 2 |
+ 1 |
+ 2 = 0 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
Σ = 1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Рис. 1: Преобразование энергии в замкнутой системе при взаимодействии двух тел
Дифференциал постоянной величины всей суммарной энергии (6) такой замкнутой системы равен нулю:
Σ = Σ1 + Σ2 =
=1 1 1 + 1 1 1 + 1 1 1 + 1 1 1 + 1 +
+2 2 2 + 2 2 2 + 2 2 2 + 2 2 2 + 2 =
=1 21 + 1 1 1 2 + 1 21 + 1 1 1 2 + 1 +
+ 2 22 + 2 2 2 2 + 2 22 + 2 2 2 2 + 2 = 0 (7)
Из (7) следует, что величины дифференциалов механических энергий пар взаимодействующих тел, взятых с противоположными знаками, всегда равны друг другу:
Σ1 = − Σ2 |
(8) |
5
Законы движения масс в стационарном поле потенциальных сил уже хорошо изучены и в полном объёме представлены практически в учебных курсах физики и теоретической механики, поэтому, что бы в дальнейшем не учитывать влияние их действия на общую массу всей замкнутой системы, остановимся исключительно только на анализе характера изменения кинетических энергии этих тел, и для этого определим второй дифференциал функции (7), который, с учётом того, что второй дифференциал отравен 0 только тогда, когда — независимая переменная или линейная функция от независимой переменной и в этом случае любой дифференциал = 0 ( ≥ 2), равен:
1 12 + 1 12 = − 2 22 − 2 22 |
(9) |
В соответствии с правилами дифференцирования, знаки в (9) указывают не на направления изменения аргументов, а на их возрастание — при знаке (+) или на их убывание — при знаке (–).
Равенство (9) представляет собой математическую форму записи закона преобразования кинетической энергии в замкнутой системе, согласно которому противоположные по знакам результиру-
ющие скорости изменения мощностей преобразования кинетических энергий поступательного и вращательного движения взаимодействующих тел всегда равны друг другу.
Преобразуя (9), видим, что сумма скоростей изменения мощностей преобразования энергий поступательного движения обоих тел всегда равна скорости изменения мощности преобразования энергии вращательного движения этих же тел, взятой с обратным знаком:
1 12 + 2 22 = − 1 12 − 2 22 |
(10) |
Следствие закона преобразования механической энергии в замкнутой системе: сумма скоростей
изменения мощностей преобразования энергий поступательного движения взаимодействующих тел всегда равна сумме скоростей изменения мощностей преобразования энергии вращательного движения этих же тел, взятой с обратным знаком.
Поскольку взаимодействуют идентичные тела, то, разделив обе части равенства (9) на 1 = 2, получаем следующий вид равенства:
12 |
12 12 |
22 |
22 |
22 |
(11) |
В замкнутой системе (рис. 1), в которой+ |
центр |
=масс− |
−Тела |
1 взаимодействует только с поверхностью |
|
вращения Тела 2, ускорение 1 вращательного движения Тела 1 равно нулю, поэтому равенство (11) принимает вид:
2 |
|
2 |
2 |
|
2 |
(12) |
|
|
1 |
|
2 |
2 |
|
2 |
|
Модули правой и левой части равенства ( |
12) равны друг другу: |
|
|||||
|
= − |
|
− |
|
|
|
|
12 = (− 22) |
+ (− 2 22) |
(13) |
|||||
Имеет место быть следующее неравенство [Фаддеев Д.К. Лекции по алгебре: Учебное пособие. 5-е изд., стер. — СПб: Издательство «Лань», 2007. — 416 стр.: илл. (Учебники для вузов. Специальная
литература. (с. 34)]:
+ ≤ +
Исходя из условия этого неравенства, модуль суммы двух величин в правой части (13), по крайней мере, равен сумме модулей этих же величин:
22 |
|
|
2 |
22 |
|
22 |
|
|
2 22 |
(14) |
||
Следовательно, сумма модулей(−слагаемых) + (− |
правой) = (−части) + равенстве(− ) |
(13) равна модулю левой части |
||||||||||
этого же равенства: |
|
|
= (− |
|
) + (− |
|
|
|
) |
|
||
А поскольку сумма двух, не равных |
12 |
22 |
2 |
22 |
(15) |
|||||||
|
|
|
|
|
|
|
|
|||||
|
нулю величин, всегда больше любой из них, то из (15) следует: |
|||||||||||
Преобразуем (12) к виду: |
|
|
12 > (− 22) |
|
|
|
(16) |
|||||
|
|
|
12 |
+ 22 |
= − 22 22 |
|
|
(17) |
||||
6

Левая часть равенства (17) характеризует собой результирующее ускорение поступательного движения общего центра масс всей замкнутой системы, для определения которого извлечём корни квадрат-
ные из обеих частей этого равенства и получаем следующий результат: |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(18) |
|||
|
|
|
|
|
|
|
|
12 |
|
22 |
|
|
|
|
|
2 |
|
2 |
|
|
|
||||||
С учётом того, что |
|
поступательного движения центра масс всей замкнутой системы |
|||||||||||||||||||||||||
, скорость± |
|
|
= ± |
|
|
|
|
+ |
|
= ± |
|
|
|
|
|
2 |
2 |
|
|
(19) |
|||||||
определяется |
зависимостью: |
|
|
|
|
|
|
12 |
22 |
|
|
|
|
|
|
|
|||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12) указывают не на их направления, а на их возрастание — при |
||||||||||||||||||||||||
А поскольку знаки ускорений±в (= ± |
|
|
|
|
= ± |
|
|
|
|
+ |
|
|
|
= ± |
|
|
|
|
|
|
|
||||||
знаке (+) или на их убывание — при знаке (–), то из (19) следует, что существую четыре равноправных равенства возможных соотношений между характером изменения (убывания или возрастания) величин ускорений поступательного и вращательного движения замкнутой изменяемой многомассовой системы тел:
|
+ |
|
|
|
2 |
|
2; |
(20) |
|
|
= + |
2 |
2; |
(21) |
|||
|
+ |
|
= − |
|
2 |
|
2; |
(22) |
|
− |
|
= + |
|
2 |
|
2 |
(23) |
Из (20), (21), (22) и (23) следует, что |
возрастание или убывание результирующего ускорения посту- |
|||||||
− |
|
= − |
|
|
|
|
|
|
пательного движения общего центра масс всей замкнутой механической системы взаимодействующих тел возможно как при убывании, так и при возрастании ортогональной по отношению к его направлению изменения составляющей результирующего ускорения 2 вращательного движения Тела 2, умноженного на его радиус 2.
Для того, чтобы определить ту величину внутренней силы замкнутой системы, которая необхо-
дима для придания общей её массе Σ |
|
1 |
|
|
2 |
заданной величины ускорения её поступательного |
|||||||||||||
движения, необходимо умножить обе |
части равенства (12) на величину всей массы |
|
|
|
этой |
||||||||||||||
|
= |
|
+ |
|
|
|
|
|
|
|
|
|
|
Σ |
|
2 |
|
||
системы и правую часть равенства ещё умножить и разделить на радиус |
|
поверхности вращения |
|||||||||||||||||
2 |
|
|
= |
|
|
||||||||||||||
Тела 2: |
|
|
|
|
2 |
|
22 |
|
|
|
2 2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
± = ±2 = ±2 |
|
|
|
|
|
= ±2 |
2 |
= ±2 |
|
|
|
|
|
(24) |
|||||
|
|
|
2 |
|
2 |
|
|
|
|
||||||||||
Из (24) следует, что величина силы тяги , приложенной к общему центру масс замкнутой системы, равна частному от деления удвоенной величины момента 2 от действия этой силы тяги , когда она приложена к поверхности вращения Тела 2 с его моментом инерции 2 = 22.
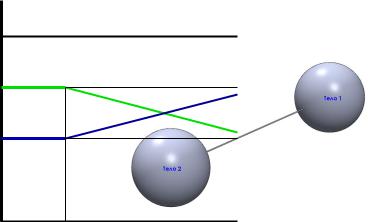
В отличие от рассмотренного случая взаимодействия центра масс одного тела с поверхностью вращения другого тела, возможно и такое взаимодействие (рис. 2), когда центр масс Тела 1 взаимодействует с центром масс Тела 2, а ускорения 1 и 2 вращательного движения Тела 1 и Тела 2 равны нулю, в результате чего равенство (11) принимает уже иной вид:
Из (25) следует: |
|
12 |
= − 22 |
|
(25) |
|
|
|
1 |
|
|
2 |
(26) |
Следовательно, и в этом случае |
существуют четыре равноправных равенства возможных соотноше- |
|||||
± |
|
= ± |
|
|
|
|
ний между характером изменения ускорений поступательного движения взаимодействующих центрами масс тел в замкнутой системе:
+ |
1 |
|
|
2; |
(27) |
1 |
= + |
2; |
(28) |
||
+ |
1 |
= − |
|
2; |
(29) |
− |
= − |
|
(30) |
||
− |
1 |
= + |
|
2 |
|
Из (27), (28), (29) и (30) следует, что возрастание или убывание ускорения поступательного движения центра масс одного из взаимодействующих тел возможно как при убывании, так и при возрастании ускорения поступательного движения центра масс второго из взаимодействующих тел.
7
Σ = 1 + 2 + 1 + 2 |
= |
|
|||
1 |
|
|
|
|
|
2 |
|
|
|
|
|
0 |
1 |
+ 2 |
+ 1 + 2 = |
|
|
Σ = 1 |
0 |
||||
Рис. 2: Преобразование энергии в замкнутой системе при взаимодействии двух тел
Умножив обе части равенств (27), (28), (29) и (30) на величину массы = 1 = 2, получаем:
|
+ |
1 |
|
|
2; |
(31) |
|
1 |
= + |
2; |
(32) |
||
|
+ |
1 |
= − |
|
2; |
(33) |
|
− |
1 |
= + |
|
2 |
(34) |
Таким образом, определённые из закона |
сохранения энергии равноправные равенства (31), (32), (33) |
|||||
− |
|
= − |
|
|
|
|
и (34) указывают на то, что действие законов Ньютона, распространяющееся только исключительно на те инерциальные системы отсчёта координат, которые не способны испытывать ускорений, не может быть распространено на общие случаи взаимодействия тел, поскольку то, что в законах Ньютона подразумевается под силами действия, равными силам противодействия, взятыми с обратными знаками, на самом деле вне систем отсчёта координат не могут являться таковыми потому, что, во-первых, одна из сил должна непременно выступать в качестве некой мнимой величины, а, во-вторых, эти силы, допускающие мнимость, не могут являться векторными направленными величинами.
При отсутствии у взаимодействующих центрами масс тел ускорений вращательного движения, равенство (9) принимает вид:
1 |
|
12 |
2 |
|
22 |
(35) |
||
Из (35) следует, что отношение масс при |
центральном взаимодействии тел обратно отношению |
|||||||
|
= − |
|
|
|
||||
квадратов их ускорений поступательного движения, взятому с противоположным знаком: |
|
|||||||
|
1 |
|
22 |
|
|
|
(36) |
|
|
2 |
= − 12 |
|
|
||||
|
|
|
|
|||||
При этом из (36) следует, что действительное отношение ускорений поступательного движения двух тел при взаимодействии их центрами масс является мнимой величиной, пропорциональной корню квадратному из обратного отношения масс взаимодействующих тел, что совершенно не соответствует
положениям третьего закона Ньютона: |
|
|
|
|
|
|
|
|
|
|
± |
2 |
= ± |
|
|
|
|
1 |
|
|
|
1 |
|
} 2 |
(37) |
|||||||
|
|
|
||||||||
Именно поэтому само представление об ускорениях поступательного движения точек в инерциальных системах отсчёта, вытекающее из законов Ньютона, является чрезвычайно упрощённым, потому что отражает лишь малую часть всех тех состояний взаимосвязанных ускорений, которые приобретают точки взаимодействующих тел в процессе изменения любых их состояний.
Например, функция радиус-вектора точки имеет вид: |
|
|||
Ñ = |
Ñ |
|
|
(38) |
|
|
|||
8
