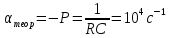Исследование свободных процессов в электрических цепях (лаба 3) / Т.Л3 (Алина)
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра Теоретических Основ Электротехники
отчет
по лабораторной работе №3
по дисциплине «Теоретические Основы Электротехники»
Тема: ИССЛЕДОВАНИЕ СВОБОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ
|
Студенты гр. 7501 |
|
Попадьина А.О. |
|
Преподаватель |
|
Гарчук А.А. |
Санкт-Петербург
2019
Цель работы:
Изучение связи между видом свободного процесса в цепи и расположением собственных частот (корней характеристического уравнения) на комплексной плоскости; приближенная оценка собственных частот и добротности RLC- контура по осциллограммам.
При
возбуждении цепи источником тока
собственные частоты можно рассчитать
как нули входной проводимости цепи
 :
:
 а)
для цепи первого порядка, представленной
на рис.1, а
а)
для цепи первого порядка, представленной
на рис.1, а
 ,
откуда
,
откуда

(1)
 б)
для цепи второго порядка, представленной
на рис. 2, б
б)
для цепи второго порядка, представленной
на рис. 2, б
 ,
откуда
,
откуда
 ,
, ,
,
(2)
в) для цепи третьего порядка, представленной
на рис. 3
 откуда
откуда
 ,
,
 ,
,
 .
.
 (3)
(3)
Общий вид решения для напряжения любого элемента цепи
 ,
,
где
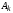 – постоянные интегрирования,
– постоянные интегрирования,
 – порядок цепи.
– порядок цепи.
У цепи первого порядка одна собственная частота отрицательная вещественная, свободный экспоненциальный процесс имеет вид
 (3.4)
(3.4)
где
 – постоянная затухания,
– постоянная затухания,
 – постоянная времени экспоненты.
Временная диаграмма свободного процесса
показана на рис. 4а, причем
– постоянная времени экспоненты.
Временная диаграмма свободного процесса
показана на рис. 4а, причем
 – интервал времени, соответствующий
любой подкасательной к экспоненте.
– интервал времени, соответствующий
любой подкасательной к экспоненте.
В цепи второго порядка две собственные
частоты могут быть разными вещественными
различными (апериодический режим;
временная диаграмма суммы двух экспонент)
кратными вещественными
 (критический режим) или комплексно-сопряженными
(колебательный режим). Вид критического
процесса
(критический режим) или комплексно-сопряженными
(колебательный режим). Вид критического
процесса
 близок к диаграмме, показанной на рис.
4б, причем момент достижения максимума
близок к диаграмме, показанной на рис.
4б, причем момент достижения максимума
 ,
если
,
если
 .
Комплексно-сопряженным частотам
соответствует качественно новый характер
свободного процесса – колебательный:
.
Комплексно-сопряженным частотам
соответствует качественно новый характер
свободного процесса – колебательный:
 ,
(3.5)
,
(3.5)
где
 – постоянная затухания,
– постоянная затухания,
 – частота затухающих колебаний (
– частота затухающих колебаний ( ).
Временная диаграмма колебательного
процесса представлена на рис. 4 в.
).
Временная диаграмма колебательного
процесса представлена на рис. 4 в.
Дальнейшее увеличение порядка цепи к
качественно новым явлениям не приводит.
Так, в схеме, изображенной на рис.3,
собственные частоты могут быть либо
три вещественные, либо одна вещественная
и две комплексно-сопряженные, например,
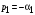 и
и
 .
Временная диаграмма свободного процесса
представлена на рис. 4 г – это сумма
экспоненты (см. пунктир) и затухающей
синусоиды.
.
Временная диаграмма свободного процесса
представлена на рис. 4 г – это сумма
экспоненты (см. пунктир) и затухающей
синусоиды.
В некоторых случаях собственные частоты относительно просто рассчитываются по осциллограммам. Например, согласно (3.4) по рис. 4 а можно рассчитать постоянную затухания
 (3.6)
(3.6)
Для случая рис. 3.3, в постоянная
затухания также может быть определена
на основании (3.6), но при этом обязательно
выполнение условия
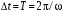 ,
что вытекает из (3.5).
,
что вытекает из (3.5).

Экспериментальные исследования свободного процесса в цепи первого порядка
3.2.1. Исследование свободных процессов в цепи первого порядка





Вопрос 1:
Осциллографируемый свободный процесс
описывается затухающей экспонентой, с
постоянной затухания, равной
 .
.


Вопрос 2:
Найденная собственная частота
соответствует осциллограмме. 

Где

3.2.2. Исследование свободных процессов в цепи второго порядка.

-
Колебательный режим


Теоретический
расчет собственной частоты:


![]()



Расчет собственной частоты по экспериментальным данным:




Расчет добротности:




-
Апериодический режим

Расчет собственной частоты:








Расчет добротности для апериодического режима:

-
Критический режим

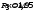



Определим корни ХП экспериментальным путем:
 (по графику)
(по графику)



Теоретический
способ:



-
Незатухающий режим


Теоретический способ





Проверка:





Расчет добротности для незатухающего режима

Вопрос 3: Общий вид аналитического выражения для описанных процессов:
![]()
Вопрос 4: Найденные по экспериментальным данным собственные частоты с небольшой погрешностью соответствуют теоретическому расчету.
Вопрос
5: Осциллограмма,
полученная для апериодического режима
не соответствует теоретическим расчетом
для

Вопрос 6: Рассчитанные значения добротностей
согласуются с теоретическими данными, значения соответствуют рассматриваемым режимам.
3. Исследование свободных процессов в цепи третьего порядка

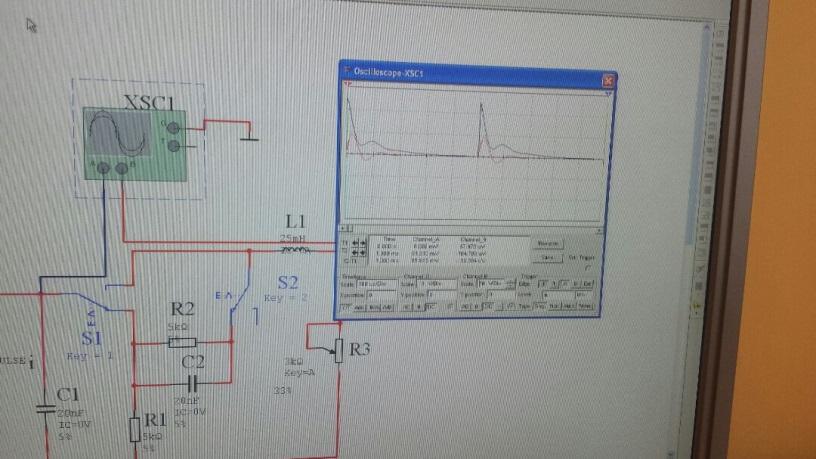
R = 5 кОм
C = 0.02 мкФ
L = 0.025 Гн
R1 = 1 кОм




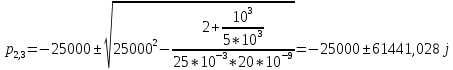
Вопрос 7: Осциллографируемый процесс
описывается аналитическим выражением: