17.Линейная скорость и ускорение при вращательном движении

Вращательное движение твердого тела.

Поступательное движение твердого тела.

При поступательном движении прямая проходящая через тело остается параллельной самой себе. Все точки при поступательном движении имеют одинаковые траектории, а следовательно одинаковую скорость и ускорение. Поэтому поступательное движение сводится к движению одной точки.

Вращательное это такое движение, при котором прямая, связанная с телом остается неподвижной. Такая прямая называется осью и задается двумя точками. Положение тела задается при помощи угла поворота. Для этого выбирают неподвижную плоскость, которая будет являться началом 

отсчета. Такой угол и является законом вращательного движения.

Угловая скорость и угловое ускорение. Угловую скорость удобно представлять в виде вектора, направленного вдоль оси вращения, в такую сторону, чтобы с конца вектора угловой скорости вращение виделось против часовой стрелки.

Угловое ускорение есть скорость изменения угловой скорость. Является производной от скорости или второй производной от угла поворота. Если вектор ускорения сонаправлен с вектором угловой скорости, то вращение ускоряющееся.

Пример. Маховик на валу двигателя разгоняется с постоянным ускорением. Определить скорость и закон движения.

18. Сложное (абсолютное) тело

Сложное движение – это такое движение, которое можно разложить на несколько простых. Простыми движениями считаются поступательное и вращательное.

При решении задач на сложное движение используют теорему о сложении скоростей.

При сложном движении точки абсолютная скорость в каждый момент времени равна геометрической сумме переносной (v_е) и относительной (v_к) скоростей.

где α – угол между векторами v_е и v_r.

Плоскопараллельным, или плоским называется такое движение твердого тела, при котором все точки тела перемещаются параллельно некоторой неподвижной в рассматриваемой системе отсчета плоскости.

Плоскопараллельное движение можно изучать, рассматривая любое плоское сечение тела, параллельное неподвижной плоскости, называемой основной.

Все точки тела, расположенные на прямой, перпендикулярной к основной плоскости, движутся одинаково.

Плоскопараллельное движение изучается двумя методами: методом разложения сложного движения на поступательное и вращательное и методом исключения скоростей.

18. Сложное(абсолютное) движение

Сложным движением называют такое движение, при котором точка одновременно участвует в двух или более движениях Абсолютным движением называют движение

точки М по отношению к ос­новной системе отсчета O₁X₁Y₁Z₁,которую условно принимают за неподвижную. От­носительным движением называют движе­ние точки М по отношению к подвижной системе отсчета OXYZ. Переносным дви­жением называют движение подвижной системы отсчета OXYZотносительно ос­новной (неподвижной) системы отсчета O₁X₁Y₁Z_1.

Теорема о сложении скоростей

Абсолютной скоростью называют скорость точки М относи­тельно основной системы координат O₁X₁Y₁Z₁ и обозначают 

Относительной скоростью называют скорость точки М относи­тельно подвижной системы координат OXYZ и обозначают 

Переносной скоростью называют скорость той точки подвиж­ной системы координат, с которой в данный момент совпада­ет движущаяся точка М, и обозначают 

Абсолютная скорость точки в сложном движении равна гео­метрической сумме переносной и относительной скоростей =+

Модуль абсолютной скорости в общем случае находят проек­тированием выражения на оси координат, так как угол между векторами относительной и переносной скоростей может быть от 0 до 180°: 

19. Плоскопараллельное движение.Плоскопараллельным (плоским) движением называется движение, при котором каждая точка тела движется в одной и той же плоскости, параллельной некоторой неподвижной плоскости, при этом расстояние от любойего точки до данной неподвижной плоскости не изменяется (Рис.1). Описание плоского движения тела сводится к описанию движения одного сечения тела относительно неподвижной плоскости. Такое сечение принято называть плоской фигурой.

Рис.1

Примерами плоскопараллельного движения являются качение катка по горизонтальной поверхности (Рис.2), движение звена АВ (шатун) кривошипно-ползунного механизма (Рис. 3), движение звена АВ (шатун) кривошипно-коромыслового механизма (Рис. 4), движение звеньев АВ и ВД (шатуны) многозвенного механизма (Рис. 5).

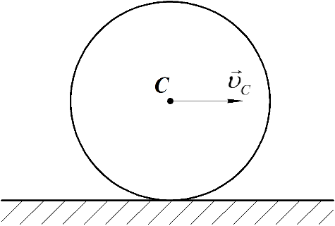
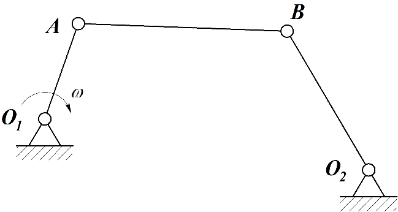
Рис. 2 Рис. 3

Рис. 4 Рис. 5