4. Аналитическое определение равнодействующей силы
Равнодействующую системы сходящихся сил можно определить и аналитически (способом проекций). Для этого необходимо воспользоваться теоремой: проекция равнодействующей на данную ось равна алгебраической сумме проекций слагаемых сил на ту же ось.
Проекции равнодействующей на координатные оси х и у определяются как суммы проекций составляющих.
Рис. 4.11
Для удобства и простоты индекс и пределы суммирования ставить не будем:
.
(4.8)
(4.9)
Зная проекции, определяют модуль и направление равнодействующей по формулам:
При решении задач на сложение плоской системы сходящихся сил аналитическим способом необходимо: выбрать систему координатных осей х и у;найти углы каждой силы с координатными осями, а затем, определив проекции равнодействующей, найти ее модуль и направление.
5. Уравнение равновесия плоской системы сходящихся сил
Система сил называется сходящейся, если линии действия всех сил системы
пересекаются в одной точке. Сходящаяся система эквивалентна одной силе, равной их геометрической сумме. Эта сила называется равнодействующей.
Так
как 
,
то для того чтобы модуль равнодействующей 
был
равен нулю, необходимо одновременное
выполнение трех равенств (1):
или 
или 
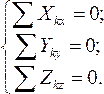(1)
Равенства (1) называются уравнениями равновесия пространственной сходящейся системы сил.
|
Если
система сил плоская сходящаяся, т.е. все
силы лежат в плоскости xy, то последнее
уравнение системы (1) выполняется
тождественно, и уравнения равновесия
примут вид: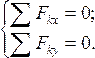 
6.Пара сил и ее действие на тело. Момент сил относительно точки и оси
Система двух равных и параллельных сил, направленных в противоположныестороны и не лежащих на одной прямой, называется парой сил. Примером такой системы сил могут служить усилия, передаваемые от рук шофера на рулевое колесо автомобиля.
Именно поэтому свойства пары как специфической меры механического взаимодействия тел изучается отдельно. Сумма проекций сил пары на любую ось равна нулю (рис. 11, а), т.е. пара сил не имеет равнодействующей. Несмотря на это тело под действием пары сил не находится в равновесии.
Рис. 11
Действие пары сил на твердое тело, как показывает опыт, состоит в том, что она стремится вращать это тело. Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние (взятое по перпендикуляру к силам) между линиями действия сил. Обозначим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютная величина момента (рис. 11, а и б) равна
M = -Pa =- P'a
M = Qa =Q’a
Кратчайшее расстояние между линиями действия сил называется плечом пары, поэтому можно сказать, что момент пары сил по абсолютной величине равен произведению одной из сил на ее плечо.
Эффект действия пары сил полностью определяется ее моментом. Поэтому пару сил можно изображать дугообразной стрелкой, указывающей направление вращения. Так как пара сил не имеет равнодействующей, ее нельзя уравновесить одной силой. Момент пары в системе СИ измеряется в ньютонометрах (Н·м) или в единицах, кратных ньютонометру: кН·м, МН·м и т.д. В технической системе единиц момент пары сил измеряется в килограмм-сила-метрах (кгс·м) или в единицах, кратных килограмм-сила-метру: тс·м, а также в дольных единицах: кгс·см и т.д.
Правило знаков моментов: Момент пары сил будем считать положительным, если пара стремится повернуть тело по направлению против хода часовой стрелки (рис.11, б), и отрицательным, если пара стремится вращать тело по ходу часовой стрелки (рис.11, а).
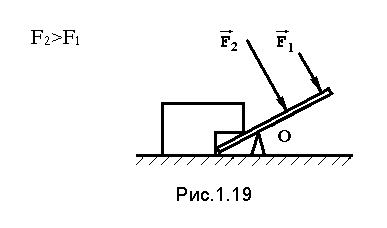
Сила может не только перемещать тело поступательно, но и оказывать на него вращательное действие, которое зависит не только от величины силы, но и от расстояния до центра поворота.
Например, для того, чтобы повернуть тело с помощью рычага (рис.1.19), наименьшую по модулю силу нужно приложить к концу рычага, чем ближе к центру, тем величина силы должна быть больше, если же сила будет проходить через точку О, то повернуть тело будет невозможно, какой большой бы она не была.
|
|
Для характеристики вращательного действия силы вводится понятие момента силы относительно точки.
Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние между точкой и линией действия силы (плечо):
(1.5)
Знак
момента определяется следующим образом:
если сила стремится повернуть тело
вокруг данной точки против часовой
стрелки, то он считается положительным
(рис.1.20), в противном случае - отрицательным.