
Тест 1 / 105 зак. сохр
..doc105 законы сохранения.
№1

Решение:
Имеем равенство масс, скоростей, радиусов
однородного шара и полой сферы ![]() .
Сравним моменты инерции тел, обозначив
их у шара
.
Сравним моменты инерции тел, обозначив
их у шара ![]() ,
у полой сферы –
,
у полой сферы – ![]() .Момент
инерции I – величина, характеризующая
распределение массы тела относительно
оси вращения и являющаяся мерой инертности
тела при вращательном движении. Вся
масса полой сферы находится на
расстоянии
.Момент
инерции I – величина, характеризующая
распределение массы тела относительно
оси вращения и являющаяся мерой инертности
тела при вращательном движении. Вся
масса полой сферы находится на
расстоянии ![]() от
оси вращения, а у шара распределена
равномерно вдоль радиуса сферы. Тогда
от
оси вращения, а у шара распределена
равномерно вдоль радиуса сферы. Тогда ![]() <
<![]() ,
следовательно,
,
следовательно, ![]() .
Значит, полая сфера поднимется на горку
выше, чем однородный шар.
.
Значит, полая сфера поднимется на горку
выше, чем однородный шар.
Ответ: 3
№2.
Решение:
Момент инерции полого цилиндра![]() ,
момент инерции сплошного цилиндра
,
момент инерции сплошного цилиндра![]() У основания
горки больше скорость сплошного цилиндра.
Но если скорость больше, то и ускорение
центра масс сплошного цилиндра больше
(поскольку из кинематики известно, что
У основания
горки больше скорость сплошного цилиндра.
Но если скорость больше, то и ускорение
центра масс сплошного цилиндра больше
(поскольку из кинематики известно, что![]() ,
гдеl –
длина горки). Поэтому для преодоления
горки сплошному цилиндру потребуется
меньше времени.
,
гдеl –
длина горки). Поэтому для преодоления
горки сплошному цилиндру потребуется
меньше времени.
Ответ: 3
№3.
Решение: Кинетическая
энергия твердого тела есть кинетическая
энергия перемещения центра масс + энергия
вращения вокруг центра масс (теорема
Кенига) Так как тела катятся без
проскальзывания, скорость их центра
масс связана с угловой скоростью вращения
простым соотношением v
= ωR. Тела скатываются с одинаковой
высоты и имеют одинаковую кинетическую
энергию, отсюда
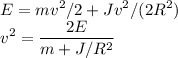 Так
как момент инерции J у полого шара больше,
чем у сплошного, его скорость будет
меньше, чем у сплошного.
Так
как момент инерции J у полого шара больше,
чем у сплошного, его скорость будет
меньше, чем у сплошного.
Ответ: 1
№4.

Решение: Потенциальная энергия Eп = mgh у основания горки полностью перейдет в кинетическую энергию Eк , причем кинетическая энергия и шара, и сферы равны между собой: Eкш = Ексф = mgh . Но кинетическая энергия этих тел состоит из энергии вращательного и поступательного
mυ 2 J ω 2
движения Eк = ____ + ____ . Здесь J – момент инерции тела. Когда нет
2 2
проскальзывания то то υ = ω R , R – радиус шара (и полой сферы).
mυ2 Jυ 2 2 R 2 mgh
mgh =_____ + __2____ . Выразим скорость тела у основания горки: υ = ________ .
2 2R mR 2 + J
Все величины, входящие в это выражение, кроме J, одинаковы и для шара, и для сферы. J сф > J ш , т.к. вся масса m распределена на периферии
2mR 2 2mR 2
( Jш =_____ , J сф =_____ ). Следовательно, числитель в выражении для скорости
5 3
шара будет больше, чем для сферы.
Поэтому скорость сферы будет меньше и быстрее скатится шар.
Ответ: 1
№5.

Решение: Момент импульса шайбы до перемещения равен моменту импульса шайбы после перемещения: L1 = L2.
По закону сохранения момента импульса получим: I1 ω1= I2 ω2 .Известно, что I = m·R2.Тогда получим:
mR12ω1 = mR22ω2. Отсюда: ω2=R12ω1/R22= ω1·(R1/ R2)2 . Так как по условию задачи R2 = 1\3R1 , то ω2 =9 ω1 .
Ответ:4
№6

Решение: Момент импульса шайбы до перемещения равен моменту импульса шайбы после перемещения: L1 = L2.
По закону сохранения момента импульса получим: I1 ω1= I2 ω2 .Известно, что I = m·R2.Тогда получим:
mR12ω1 = mR22ω2. Отсюда: ω2=R12ω1/R22= ω1·(R1/ R2)2 . Так как по условию задачи R2 = 3R1 , то ω2 =1\9 ω1 .
Ответ:1
№7.
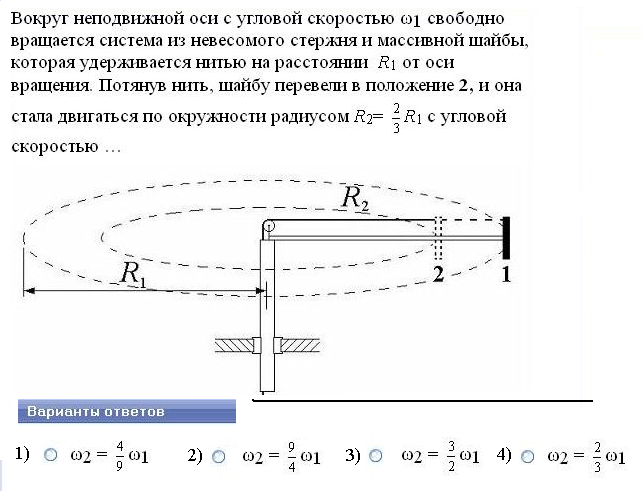
Решение: Момент импульса шайбы до перемещения равен моменту импульса шайбы после перемещения: L1 = L2.
По закону сохранения момента импульса получим: I1 ω1= I2 ω2 .Известно, что I = m·R2.Тогда получим:
mR12ω1 = mR22ω2. Отсюда: ω2=R12ω1/R22= ω1·(R1/ R2)2 . Так как по условию задачи R2 = 2\3R1 , то ω2 =9\4 ω1 .
Ответ:2
№8.

Решение: Момент импульса шайбы до перемещения равен моменту импульса шайбы после перемещения: L1 = L2.
По закону сохранения момента импульса получим: I1 ω1= I2 ω2 .Известно, что I = m·R2.Тогда получим:
mR12ω1 = mR22ω2. Отсюда: ω2=R12ω1/R22= ω1·(R1/ R2)2 . Так как по условию задачи R2 = 1\2R1 , то ω2 =4 ω1 .
Ответ:1
№9.
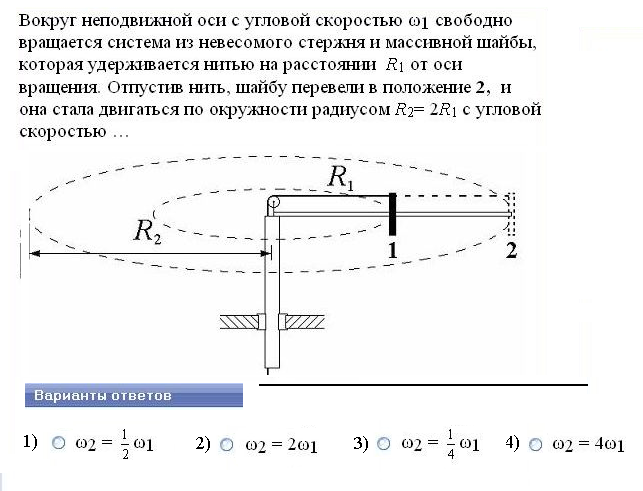
Решение: момент импульса шайбы до перемещения равен моменту импульса шайбы после перемещения: L1 = L2. Момент импульса твердого тела равен произведению момента инерции тела на угловую скорость: L = I ω, поэтому по закону сохранения момента импульса получим: I1 ω1= I2 ω2 . Шайбу можно рассматривать как материальную точку, момент инерции которой равен произведению массы на квадрат её расстояния до оси вращения: I = m·R2.Тогда получим:
mR12ω1 = mR22ω2. Отсюда: ω2=R12ω1/R22= ω1·(R1/ R2)2 . Так как по условию задачи R2 = 2R1 , то ω2 = ω1 /4.
Ответ:3
№10.

Решение: Момент импульса шайбы до перемещения равен моменту импульса шайбы после перемещения: L1 = L2.
По закону сохранения момента импульса получим: I1 ω1= I2 ω2 .Известно, что I = m·R2.Тогда получим:
mR12ω1 = mR22ω2. Отсюда: ω2=R12ω1/R22= ω1·(R1/ R2)2 . Так как по условию задачи R2 = 3\2R1 , то ω2 =4\9 ω1 .
Ответ:3
№11

Решение: Учтём,
что в начале движения поступательное
и вращательное движения цилиндра
отсутствуют, то естьυс02=0, ωс02=0:![]() .
Угловая скорость относительно оси
вращения, проходящей через центр масс
цилиндра, и скорость центра масс цилиндра
связаны соотношением
.
Угловая скорость относительно оси
вращения, проходящей через центр масс
цилиндра, и скорость центра масс цилиндра
связаны соотношением![]() .
После подстановки имеем:
.
После подстановки имеем:![]() ,
откуда модуль скорости центра масс
цилиндра у основания горки равен:
,
откуда модуль скорости центра масс
цилиндра у основания горки равен: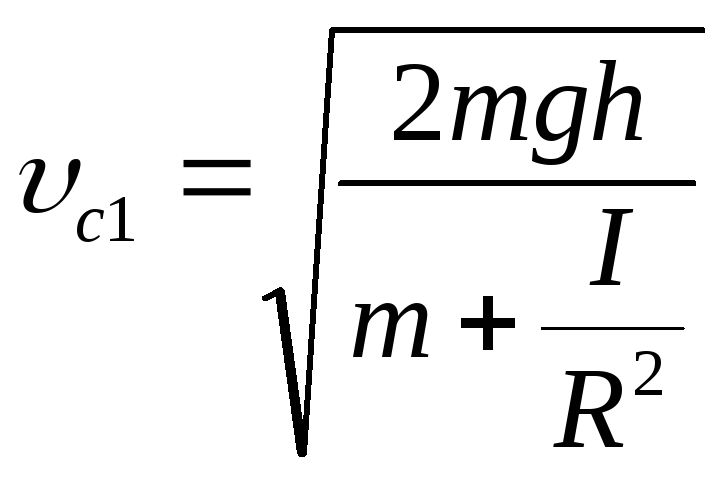 . Момент
инерции полого цилиндра
. Момент
инерции полого цилиндра![]() ,
момент инерции сплошного цилиндра
,
момент инерции сплошного цилиндра![]()
В
итоге с учётом условия, что массы,
начальные скорости и радиусы цилиндров
совпадают: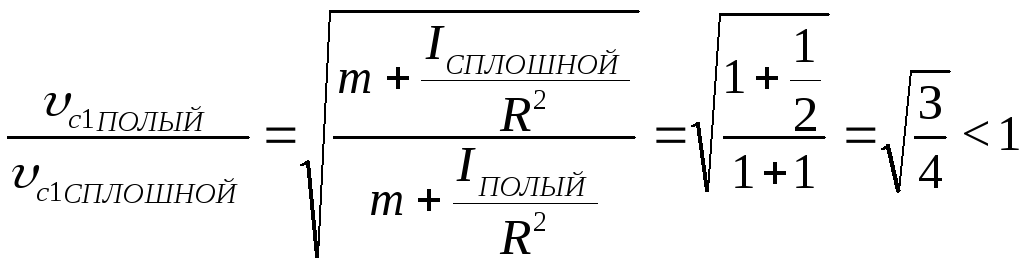 .
.
В итоге Vполый < Vсплошной т. е. больше скорость сплошного цилиндра.
Ответ:3
