КОЭ-01 - Определения. Коэффициенты Эйнштейна
.pdf
31
Виды рассеяния
Рэлеевское рассеяние - изменяется только поляризация и направление распространения волны, а энергия фотона (длина волны) остается неизменной
ħω = ħω', α1 ≠ α2, k1 ≠ k2 (но |k1| ≈ |k2|)
Комптоновское рассеяние (эффект Комптона) - малое изменение энергии фотона (длины волны), зависящее от угла рассеяния (между k1 и k2)
Эффект отдачи при больших импульсах (гамма-диапазон)
ħω ≈ ħω', ħω = ħω' – ħω → 0
Комбинационное (рамановское) рассеяние -
сравнительно большое изменение энергии фотона (длины волны), не зависящее для изотропных сред от
угла рассеяния |
ħω ≠ ħω', ħω' = ħω – (E1 – E0). |
Вынужденное комбинационное рассеяние (>106 В/см)
32
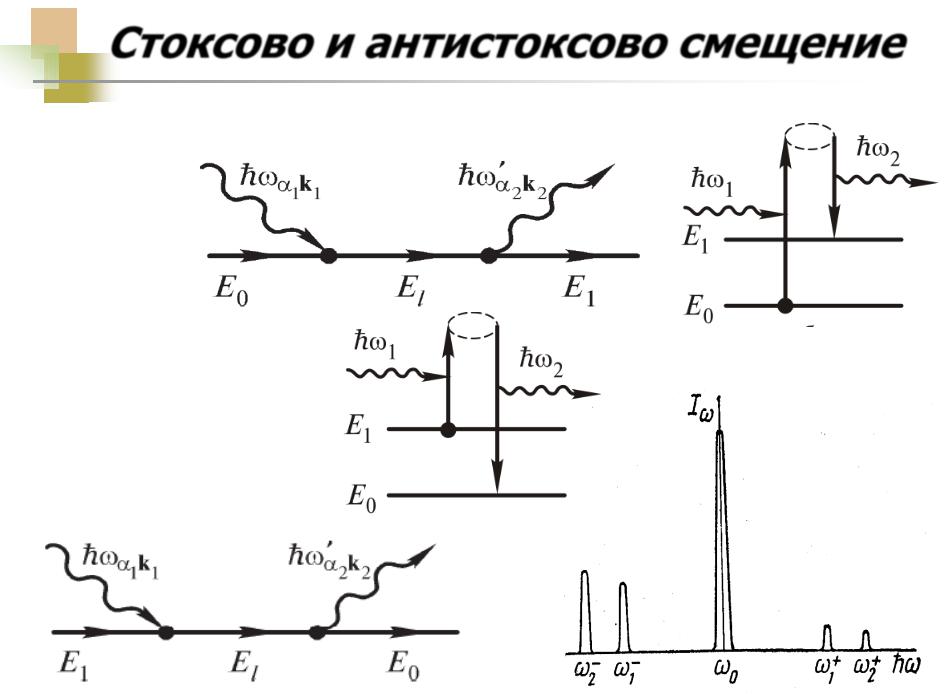
Стоксово и антистоксово смещение
Стоксово
Антистоксово
33
Рассеяние Мандельштама-Бриллюэна
Комбинационное рассеяние на периодических неоднородностях
На звуковой волне со скоростью υ и длиной Λ
Гиперзвук f = 109…1010 Гц
f/
ν - f (стоксов) и ν + f (антистоксов) сдвиги
34
Оптические
характеристики
вещества
35
Комплексный показатель преломления
Поляризованная волна |
|
|
iω t |
|
|
|
|
|
|
nz |
|
|
|
|
|
ˆ |
|
в среде |
E |
|
E e |
c |
|
|
x |
0 |
|
|
|
|
|
|
|
||
Комплексный показатель преломления
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σμ0 |
|
n |
|
n |
|
iχ |
|
ˆ |
2 ˆ |
|
|
|
2 |
|
|
|
|
|
|
|||
|
r |
|
|
|
0 |
r |
|
0 |
|
|
|
|||||||||
ˆ |
|
|
|
|
|
(n) |
ε |
|
|
c |
|
|
ε |
ε |
μ |
|
|
i |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комплексная диэлектрическая проницаемость
|
|
|
|
|
ˆ |
ˆ2 |
|
n |
|
iχ |
2 |
n |
2 |
χ |
2 |
2inχ |
|
|
||||||||
|
|
|
|
|
εr |
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε2 |
|
σ |
2nχ |
ˆ |
|
ε1 |
|
iε2 |
|
|
|
ε1 |
|
εr |
|
n |
2 |
|
χ |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
εr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε0ω |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
36
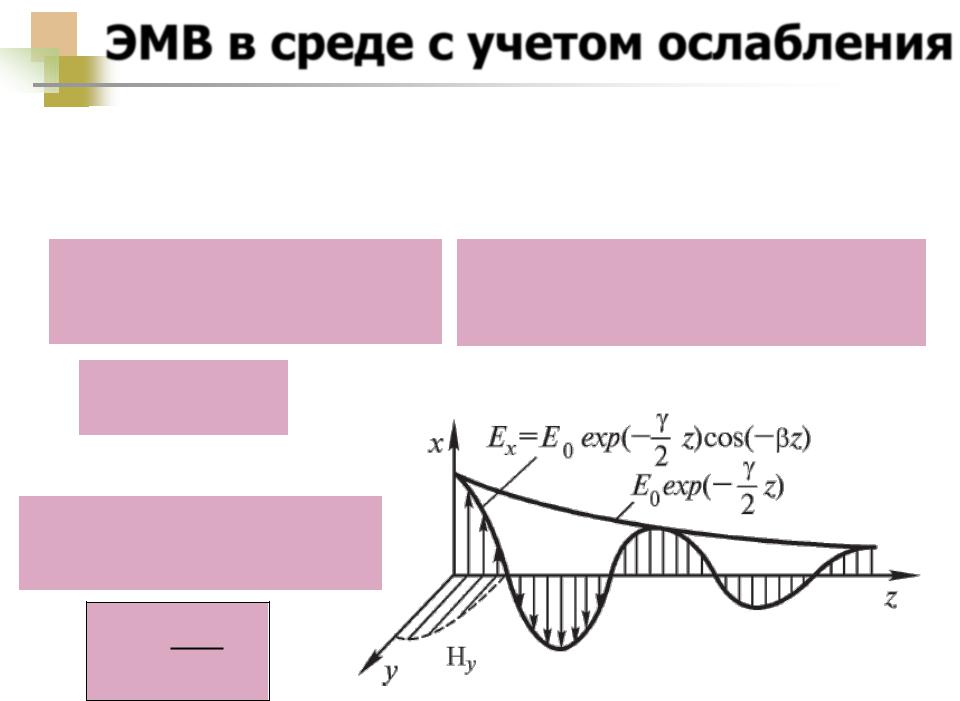
ЭМВ в среде с учетом ослабления
В среде волна, распространяется со сниженной фазовой скоростью с/n, угловой частотой и испытывает ослабление
|
|
|
|
|
|
ωχz |
|
|
ωnz |
|
γ |
|
|||||
|
|
|
|
|
|
|
|
|
i |
ωt |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||||||||
Ex E0e |
|
c e |
|
c |
|
Ex E0e |
2 |
cos(ωt βz) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ |
|
ωχ |
; β |
|
ωn |
|
|
|
|
|
|
|
|
|
|
|
2 |
c |
|
c |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ωχz |
|
|
ωnz |
||
H |
|
H |
|
|
|
|
i |
ωt |
|
|
|
|
|
|
|||||||
y |
0 |
e |
c e |
|
c |
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
H0 cnμˆ 0 E0
37
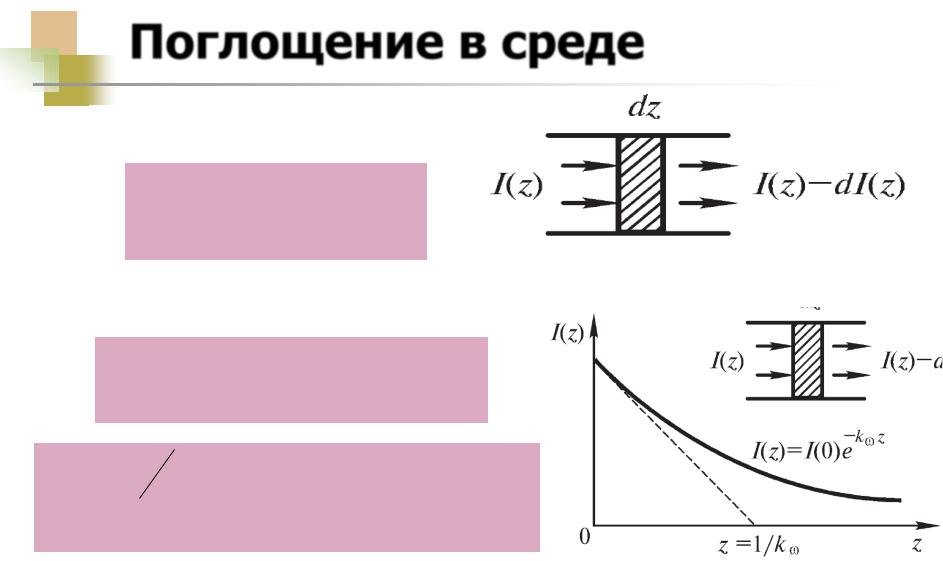
Поглощение в среде
Интенсивность
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
2 z |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
I ~ |
E |
|
|
E0 e |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-dI(z) = kωI(z)dz |
|
Закон Бугера-Ламберта |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
I (z) I |
|
|
|
|
|
|
|
I |
|
|
|
e k z |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
0 |
e |
|
c |
0 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
dI I |
|
2 |
|
|
4 |
|
4 |
|
1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
dz |
|
c |
|
|
|
c |
|
|
|
|
|
0 |
lф |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
kω - натуральный показатель поглощения на частоте ω или просто показатель поглощения
χ - главный показатель поглощения или коэффициент экстинкции
38
Оптическое сечение поглощения
При поглощении на примеси (активаторе)
kω ~ N
Оптическое сечение поглощения
k N
Интегральное сечение поглощения
Интегрирование по контуру спектральной линии g(ω)
æd N1 k d
39
Показатели преломления
n – абсолютный показатель преломления
Всегда больше 1
Обозначение – с одним индексом n1 или
n c |
||
просто без индекса n |
|
|
1 |
|
|
v1 |
||
|
||
n12 – относительный показатель преломления
Может быть и больше, и меньше 1
Обозначение – с двумя индексами n12
n12 n1 v2 1 n2 v1 n21
40
Законы преломления
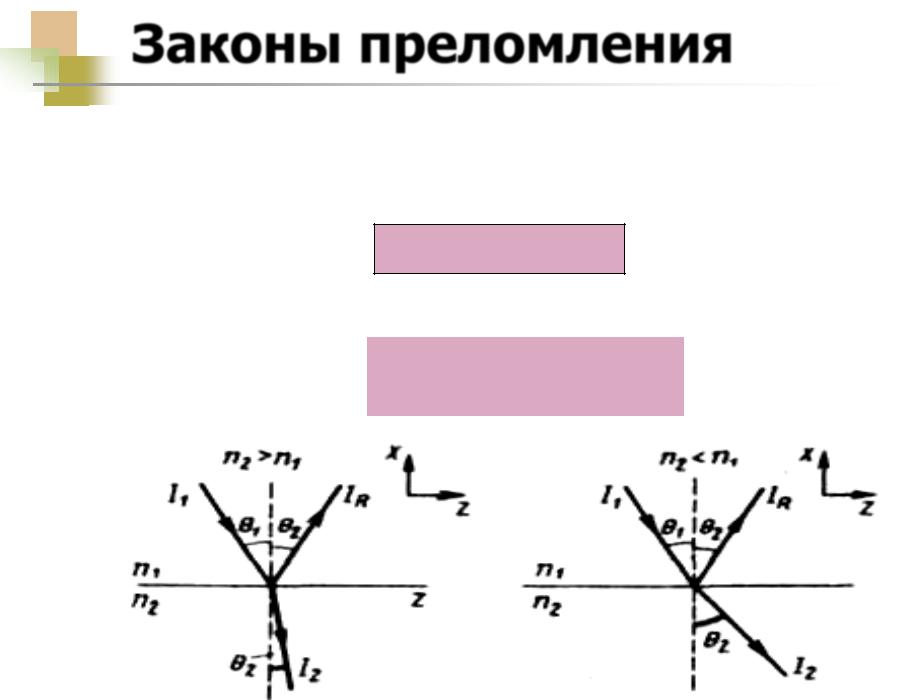
Частота электромагнитных колебаний не меняется и произведение nsinθ одинаково как для падающего (индекс 1), так и для преломленного (индекс 2) лучей
n1 sin θ1 n2 sin θ2 ,
Закон преломления Снелля (Снеллиуса)
|
|
sin θ2 |
|
v2 |
|
n1 |
n |
|
1 |
, |
|
|
|
|
|
|
|
||||||
|
|
sin θ1 |
|
v1 |
|
n2 |
12 |
|
n21 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|