Laboratornaya_Rabota_Fkhot_1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра микро и наноэлектроники

Отчёт по лабораторной работе №1

«Моделирование диаграмм состояния полупроводниковых систем с неограниченной растворимостью компонентов в жидкой и твердой фазах»

Студент гр. 4206		Петросян Л.Б.
		Базаня
Преподаватель		Александрова О.А.

Санкт-Петербург

2016

Цель работы – изучение фазовых равновесий в бинарных полупроводниковых системах с непрерывным твердым раствором методом компьютерного моделирования; расчет параметров межатомного взаимодействия; выбор моделей растворов, адекватно описывающих экспериментальную Т-х проекцию диаграммы состояния

В лабораторной работе исследовался твердый раствор CdTe – ZnTe.

Исходные данные (температуры плавления, энтальпии плавления и координаты точек ликвидуса и солидуса) представлены на рисунке 1.

Рисунок 1 - Исходные данные

1. T-x проекция диаграммы состояния.

Рисунок 2 - Т-х диаграмма, полученная в ходе лабораторной работы. (Зеленая кривая - эксперимент; Красная кривая - оптимизированная)

Оптимальными значениями параметров взаимодействия (при которых СКО наименьшее) являются . Отклонение экспериментальной кривой и оптимизированной не превышает 1%.

2. T-x проекция диаграммы состояния при обратном знаке параметров взаимодействия

Рисунок 3 - Т-х диаграмма, при обратном знаке параметров взаимодействия (Зеленая кривая - эксперимент; Красная кривая - оптимизированная)

3. Термодинамические функции смешения

Построим концентрационные зависимости термодинамических функций смещения раствора, в соответствии с теорией Дж. Гильдебранда:

1. Жидкий раствор

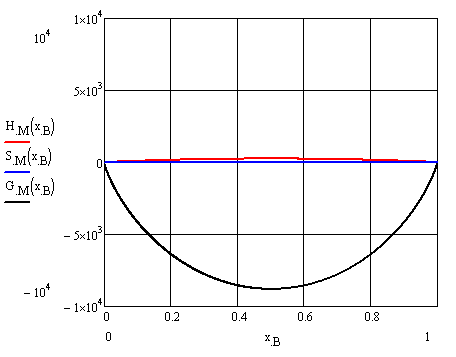
Рисунок 4 –

Рисунок 5 – Концентрационные зависимости энергии Гиббса для механической смеси (жидкий раствор)

2. Твердый раствор

Рисунок 6 -

Рисунок 7 – Концентрационные зависимости энергии Гиббса для механической смеси (твердый раствор)

4. Активности компонентов и их коэффициенты активностей

Построим (а также сравним с классической теорией) концентрационные зависимости коэффициентов активностей и активностей компонентов в твердом и жидком растворах при Т=const, согласно теории активности Льюиса:

1. Жидкий раствор

а)	б)
Рисунок 8 – Концентрационные зависимости активностей компонентов в жидком растворе a) А (CdTe), б) B (ZnTe)

а)	б)
Рисунок 9 – Концентрационные зависимости коэффициентов активностей компонентов в жидком растворе a) А (CdTe), б) B (ZnTe)

2. Твердый раствор

а)	б)
Рисунок 10 – Концентрационные зависимости активностей компонентов в твердом растворе a) А (CdTe), б) B (ZnTe)

а)	б)
Рисунок 11 – Концентрационные зависимости коэффициентов активностей компонентов в твердом растворе a) А (CdTe), б) B (ZnTe)

5. Температурная зависимость коэффициента активности компонентов A и B в твердом растворе.

Температурные зависимости будем строить для разных составов раствора

Рисунок 11 – Температурная зависимость коэффициента активности компонентов А и В при

Рисунок 12 – Температурная зависимость коэффициента активности компонентов А и В при

Рисунок 13 – Температурная зависимость коэффициента активности компонентов А и В при

6. Равновесные коэффициенты распределения компонентов А и В

Коэффициенты распределения рассчитаем, используя Т-х диаграмму состояния. Коэффициент распределения находится по формуле

Рассчитывать будем при температуре равной .

Рисунок 14 – Расчёт коэффициентов распределения

Для компонента B ; для компонента A

.

Следовательно, коэффициенты распределения равны: