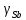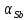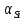Юра_2
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра МНЭ
ЛАБОРАТОРНАЯ РАБОТА №2
по дисциплине «Физико-химические основы технологии изделий электроники и наноэлектроники»
Тема: моделирование диаграмм состояния с ограниченной растворимостью компонентов (полупроводник- примесь)
|
Студент гр. 4209 |
|
Розкалий Ю. С. Самоделов А. П. |
|
Преподаватель |
|
Максимов А. И. |
Санкт-Петербург
2016
Содержание
1.Цель работы 3
2.T- x проекции исследованной диаграммы состояния 3
3.Расчет и сравнение линии ликвидуса в рамках модели идеального, регулярного, квазирегулярного растворов 6
4.Концентрационные зависимости коэффициентов активности компонентов 7
5.Равновесный коэффициент распределения компонента (примесь) 9
6.Рассчитать и построить спинодали при температурах от комнатной до плавления 10
7.Вывод 11
-
Цель работы
Изучение фазовых равновесий в бинарной
системе полупроводник (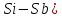 -
примесь методом компьютерного
моделирования; расчет параметров
межатомного взаимодействия; выбор
моделей растворов, адекватно описывающих
экспериментальные
-
примесь методом компьютерного
моделирования; расчет параметров
межатомного взаимодействия; выбор
моделей растворов, адекватно описывающих
экспериментальные
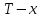 -
диаграммы состояния; расчет спинодалей
и определение областей устойчивого и
метастабильного состояний твердых
растворов в заданной системе.
-
диаграммы состояния; расчет спинодалей
и определение областей устойчивого и
метастабильного состояний твердых
растворов в заданной системе.
-
T- x проекции исследованной диаграммы состояния
-
Для жидкого раствора

Рисунок 1. T- x диаграмма состояния (жидкий раствор)
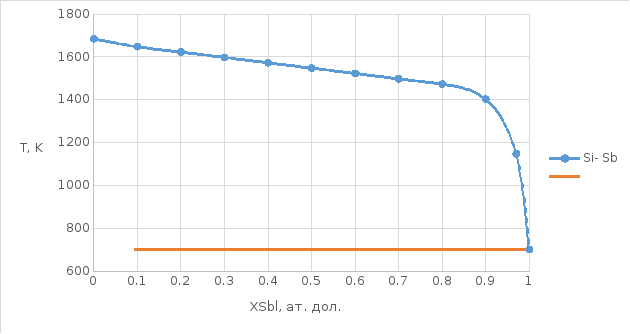
Рисунок 2. T- x диаграмма состояния (полулогарифмический масштаб жидкий раствор)
-
Для твердого раствора
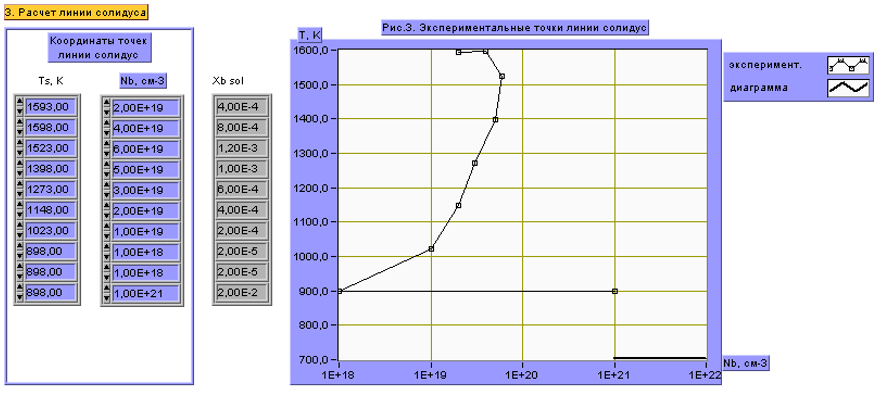
Рисунок 3. T- x диаграмма состояния (твердый раствор)
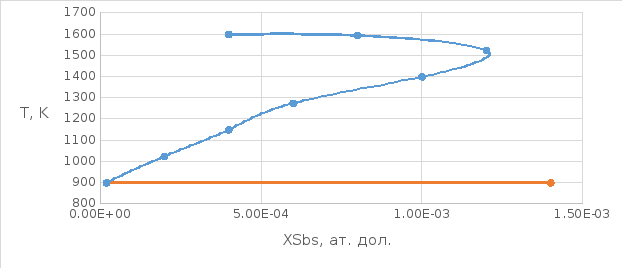
Рисунок 4. T- x диаграмма состояния (твердый раствор)
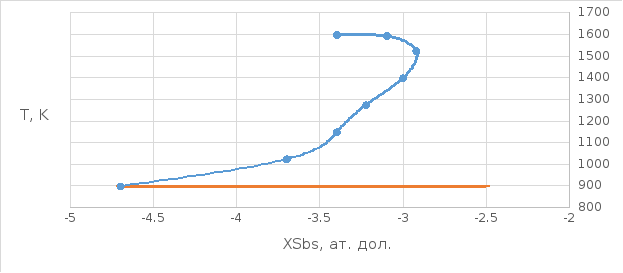
Рисунок 5. T- x диаграмма состояния (полулогарифмический масштаб твердый раствор)
![]()

-
Расчет и сравнение линии ликвидуса в рамках модели идеального, регулярного, квазирегулярного растворов
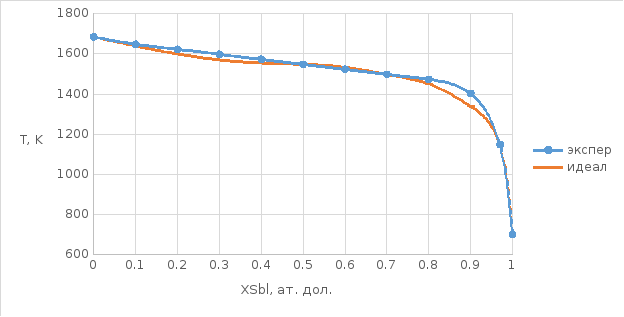
Рисунок 6. T- x диаграмма состояния системы Si-Sn
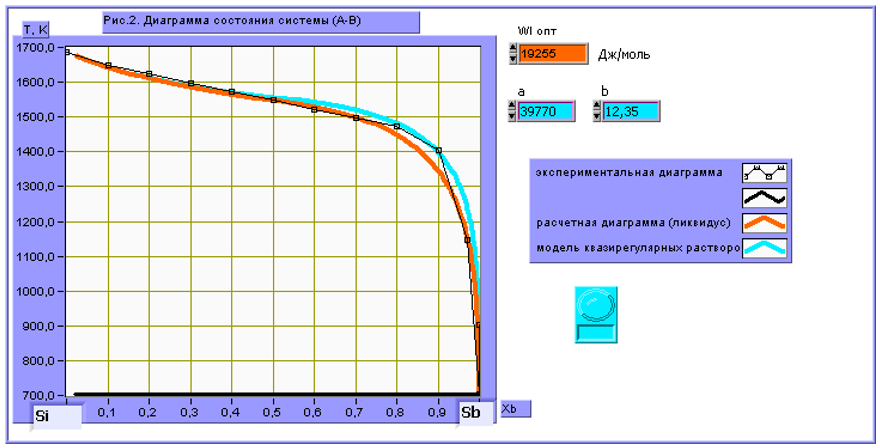
Рисунок 7. T- x диаграмма состояния (жидкий раствор)
Данную систему можно описать как при помощи регулярной модели, так и при помощи модели квазирегулярного раствора. Из рисунка 7 видно, что 3 кривые практически совпадают, с их помощью можно достаточно точно описать систему.
-
Концентрационные зависимости коэффициентов активности компонентов
-
Для жидкого раствора
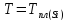 =1685
K
=1685
K

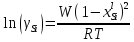
Таблица 1
|
T, K |
|
|
|
|
|
1685 |
0 |
1 |
1,375126 |
0 |
|
1648 |
0,1 |
0,9 |
1,113852 |
0,013751 |
|
1623 |
0,2 |
0,8 |
0,880081 |
0,055005 |
|
1598 |
0,3 |
0,7 |
0,673812 |
0,123761 |
|
1573 |
0,4 |
0,6 |
0,495045 |
0,22002 |
|
1548 |
0,5 |
0,5 |
0,343782 |
0,343782 |
|
1523 |
0,6 |
0,4 |
0,22002 |
0,495045 |
|
1498 |
0,7 |
0,3 |
0,123761 |
0,673812 |
|
1473 |
0,8 |
0,2 |
0,055005 |
0,880081 |
|
1403 |
0,9 |
0,1 |
0,013751 |
1,113852 |
|
1148 |
0,97 |
0,03 |
0,001238 |
1,293856 |
|
700 |
1 |
0 |
0 |
1,375126 |
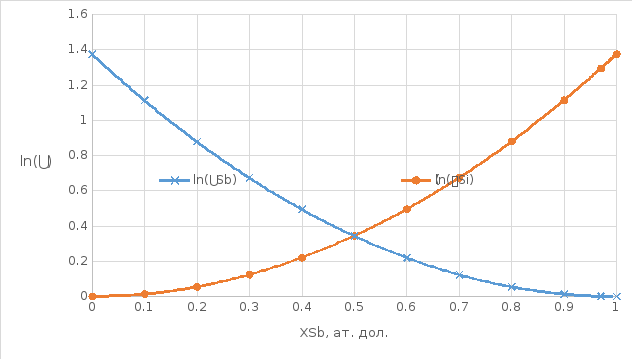
Рисунок 8. Зависимость коэффициента активностей от концентрации в жидком растворе
-
Для твердого раствора
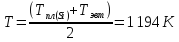
Таблица 2
|
|
|
|
|
|
|
|
0,9 |
0,1 |
0,013751 |
1,113852 |
0 |
1 |
|
0,91 |
0,09 |
0,011139 |
1,138742 |
0,312321 |
0,945328 |
|
0,92 |
0,08 |
0,008801 |
1,163907 |
0,498707 |
0,976709 |
|
0,93 |
0,07 |
0,006738 |
1,189347 |
0,6105 |
1,104506 |
|
0,94 |
0,06 |
0,00495 |
1,215062 |
0,679772 |
1,367327 |
|
0,95 |
0,05 |
0,003438 |
1,241052 |
0,726919 |
1,848996 |
|
0,96 |
0,04 |
0,0022 |
1,267316 |
0,765365 |
2,712415 |
|
0,97 |
0,03 |
0,001238 |
1,293856 |
0,804557 |
4,241222 |
|
0,98 |
0,02 |
0,00055 |
1,320671 |
0,851955 |
6,746131 |
|
0,99 |
0,01 |
0,000138 |
1,347761 |
0,914987 |
10,72494 |
|
1 |
0 |
0 |
1,375126 |
0,971764 |
22,88362 |

Рисунок 10. Зависимость коэффициента активностей в твердом растворе
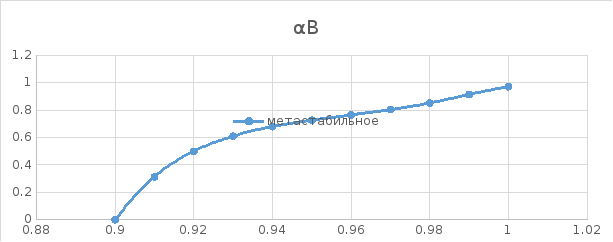
Рисунок 11. Зависимость коэффициента активностей в твердом растворе
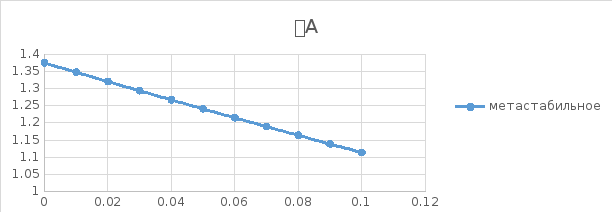
Рисунок 12. Зависимость коэффициента активностей в твердом растворе
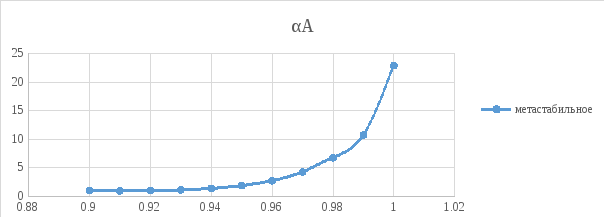
Рисунок 13. Зависимость коэффициента активностей в твердом растворе
-
Равновесный коэффициент распределения компонента
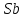 (примесь)
(примесь)
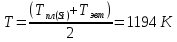
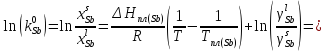
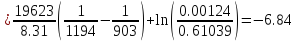
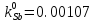
-
Рассчитать и построить спинодали при температурах от комнатной до плавления
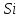
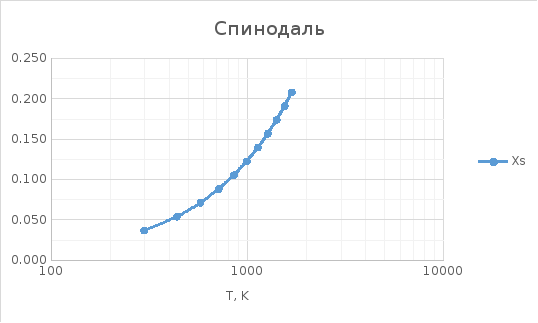
Рисунок 14. Зависимость спинодали от температуры
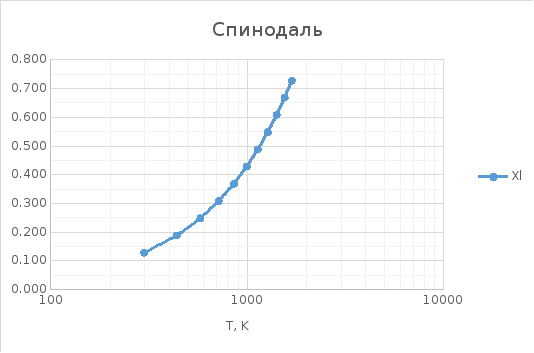
Рисунок 15. Зависимость спинодали от температуры
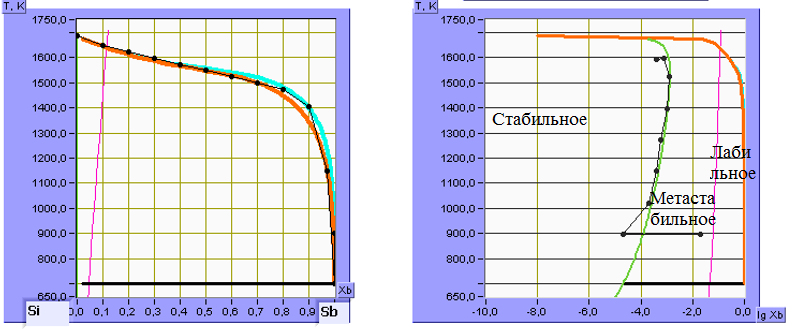
Рисунок 16. T- x диаграмма состояния

-
Вывод
В лабораторной работе произведены построения T- x диаграммы состояния для
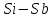 по исходным данным, подобраны оптимальные
значения параметров межатомного
взаимодействия для твердого и жидкого
раствора. В рамках модели идеального
раствора построена линия ликвидуса.
При сравнении ее с линиями, построенными
в моделях регулярного и квазирегулярного
растворов было выявлено, что они описывают
ее достаточно точно. Поэтому для описания
жидкого раствора возможно
по исходным данным, подобраны оптимальные
значения параметров межатомного
взаимодействия для твердого и жидкого
раствора. В рамках модели идеального
раствора построена линия ликвидуса.
При сравнении ее с линиями, построенными
в моделях регулярного и квазирегулярного
растворов было выявлено, что они описывают
ее достаточно точно. Поэтому для описания
жидкого раствора возможно
применение
как модели регулярного, так и
квазирегулярного растворов. Для описание
твердого раствора возможно применение
модели регулярного раствора, что видно
из рисунка 16. Рассчитаны и построены
концентрационные зависимости коэффициента
активности в твердом и жидком растворе.
Определен коэффициент равновесного
распределение примеси-
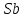 в твердом и жидком растворе. На рисунке
16 определены области стабильного,
метастабильного и лабильного фазового
состояния системы.
в твердом и жидком растворе. На рисунке
16 определены области стабильного,
метастабильного и лабильного фазового
состояния системы.

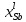 ,
ат. дол.
,
ат. дол.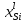 ,
ат. дол.
,
ат. дол.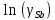
 ,
ат. дол.
,
ат. дол. ,
ат. дол.
,
ат. дол.