fkhot_2

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра МНЭ

отчет

по лабораторной работе №2

по дисциплине «физико-химические основы технологии»

Тема: МОДЕЛИРОВАНИЕ ДИАГРАММ СОСТОЯНИЯ С ОГРАНИЧЕННОЙ РАСТВОРИМОСТЬЮ КОМПОНЕНТОВ (полупроводник-примесь)

Студент гр. 4209		Бугаев Н.А.
Преподаватель		Максимов А.И.

Санкт-Петербург

2016

Цель работы: изучение фазовых равновесий в бинарной системе полупроводник (Si, Ge) – примесь методом компьютерного моделирования; расчёт параметров межатомного взаимодействия; выбор моделей растворов, адекватно описывающих экспериментальные T-x-диаграммы состояния; расчёт спинодалей и определение областей устойчивого и метастабильного состояний твёрдых растворов в заданной системе.

Основные сведения

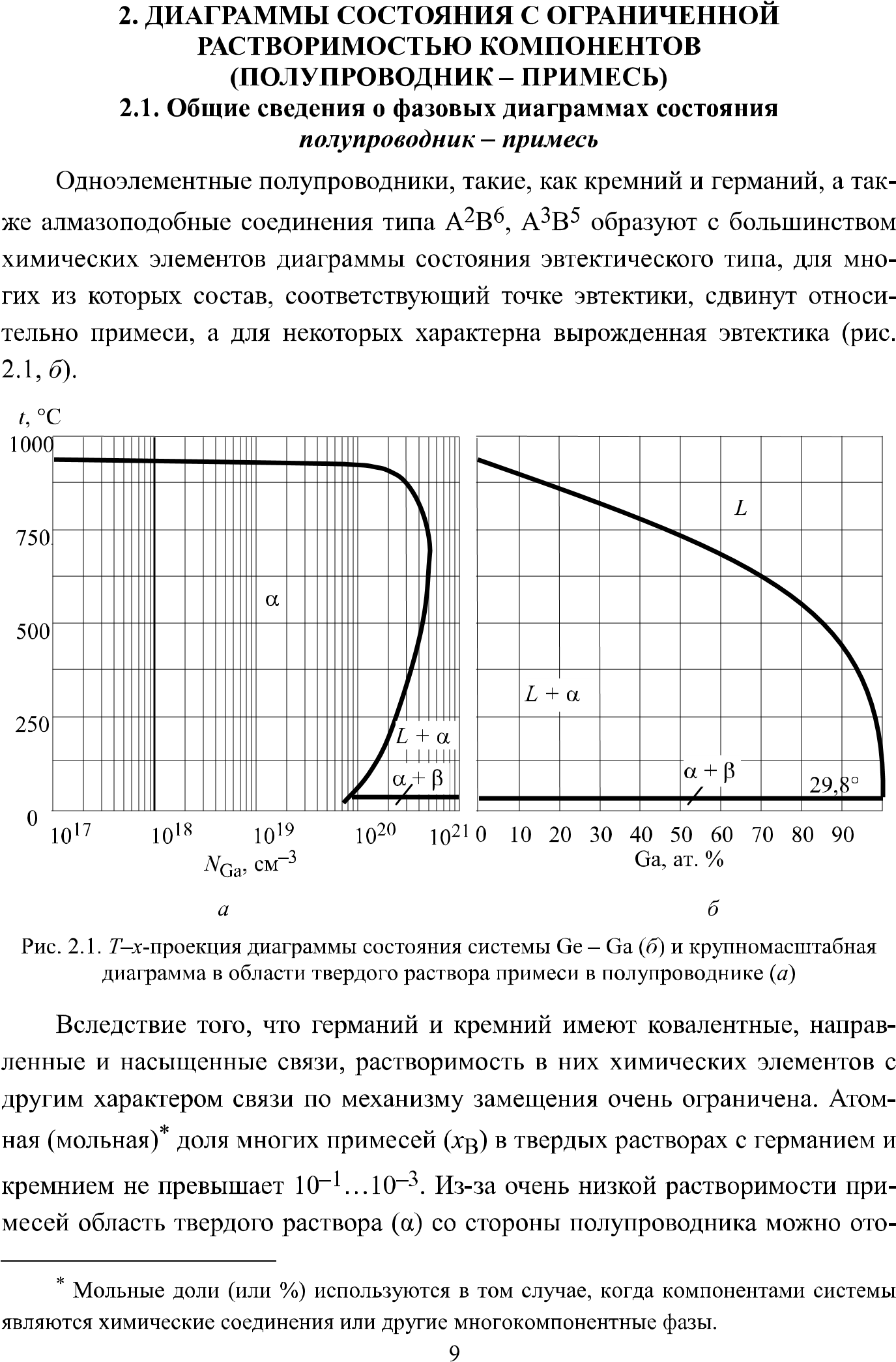
Обработка результатов.

1. Полученные диаграммы состояния и подобранные значения оптимальных параметров взаимодействия в твёрдом и жидком растворах.

Wlопт = -12696

Wsопт = 112968

2. Расчёт и построение линии ликвидуса в рамках модели идеального раствора, а также сравнение полученных линий с экспериментальной.

Таблица 1

T, K	Xbl
1680	0
1648	0,08
1623	0,13
1573	0,23
1498	0,36
1423	0,49
1348	0,59
1223	0,74
1198	0,77
1680	0,01

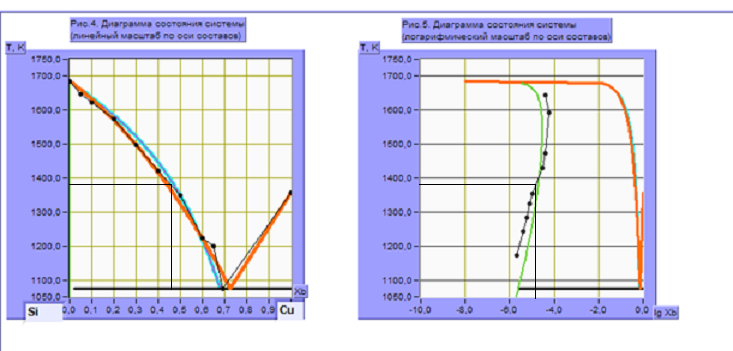
Рис.1. Диаграмма состояния для линий ликвидуса, полученных через различные модели.

Для наиболее адекватного описания экспериментальной линии ликвидуса подходят две модели растворов: квазирегулярный и регулярный растворы, так как линии, полученные с помощью них, наиболее приближены к экспериментальной кривой.

3.Рассчитаем и построим концентрационные зависимости коэффициентов активностей компонентов в твердом растворе при Т=( Т_пл(А) + Т_эвт)/2 в пределах области растворимости, а также жидком растворе во всем диапозоне составов от х=0 до 1 при Т=Т_пл(А). На тех же рисунках построены зависимости, соответствующие модели идеального раствора.

3.1. Коэффициенты активности компонентов в твердом растворе при Т=(Т_пл(А)+Т_эвт)/2 в пределах области растворимости представлены в таблице 2. Т=( Т_пл(А) + Т_эвт)/2=1380 K

Lnγ_i=W(1-x_i)²/(RT), где W^s_opt=112968 Дж/моль

На рисунке 2 представлены концентрационные зависмости коэффициентов активностей компонентов в твердом растворе в пределах области растворимости.

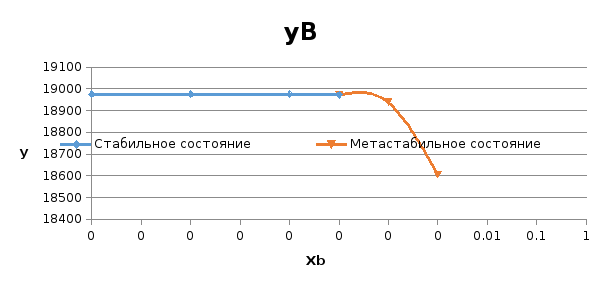
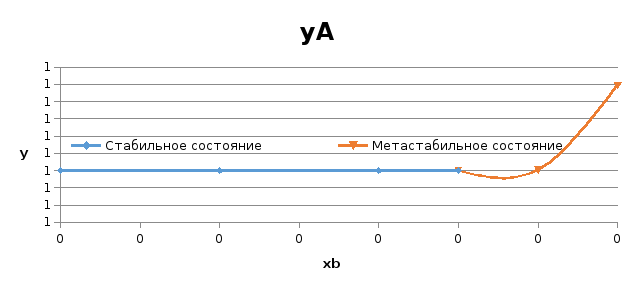
Рис.2. Концентрационные зависмости коэффициентов активностей компонентов в твердом растворе в пределах области растворимости

На рисунках 3, 4 представлены концентрационные зависимости активностей компонентов В и А в твердом растворе в пределах области растворимости соответственно.

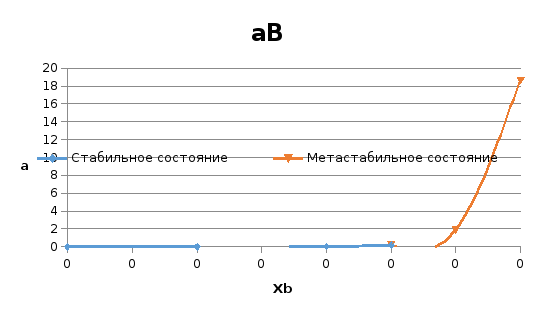
Рис.3. Концентрационная зависимость активности компонента В в твердом растворе в пределах области растворимости

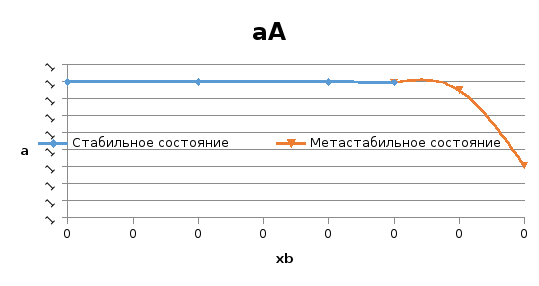
Рис.4. Концентрационные зависимости активностей компонента А в твердом растворе в пределах области растворимости

3.2.Коэффициенты активностей компонентов в жидком растворе во всем диапозоне составов от х=0 до 1 при Т=Т_пл(А)=1685 К представлены в таблице2.

Lnγ_i=W(1-x_i)²/(RT), где W^l_opt=-12696 Дж/моль

Таблица 2.

x	yB	aB
0	0,330516	0
0,1	0,407893	0,040789279
0,2	0,492361	0,098472118
0,3	0,581305	0,174391633
0,4	0,671289	0,268515487
0,5	0,758225	0,379112551
0,6	0,837666	0,502599522
0,7	0,905164	0,633614893
0,8	0,956682	0,765345781
0,9	0,98899	0,890091053
1	1	1

x	yA	aA
0	1	1
0,1	0,98899	0,890091
0,2	0,956682	0,765346
0,3	0,905164	0,633615
0,4	0,837666	0,5026
0,5	0,758225	0,379113
0,6	0,671289	0,268515
0,7	0,581305	0,174392
0,8	0,492361	0,098472
0,9	0,407893	0,040789
1	0,330516	0

На рисунке 5 показаны концентрационные зависимости коэффициентов активностей компонентов в жидком растворе во всем диапозоне составов от х=0 до 1.

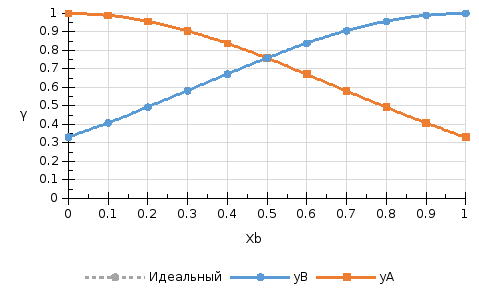
Рис.5. Концентрационные зависимости коэффициентов активностей компонентов в жидком растворе во всем диапозоне составов от х=0 до 1

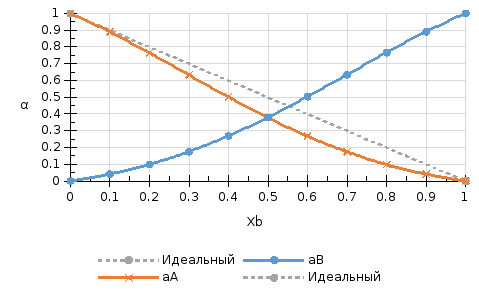
Рис.5. Концентрационные зависимости активностей компонентов в жидком растворе во всем диапозоне составов от х=0 до 1

4. Расчёт равновесного коэффициента распределения компонента В (примесь) при 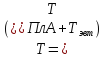/2.

Используя Т-х проекцию диаграммы состояния, при данной температуре определим состав:

T=(1685+1075)/2=1380K

Используя Т-х проекцию диаграммы состояния, при данной температуре определим состав:

Lg(Х_b^s )= -5

Х_b^l =0.45

Х_b^s =0.00001

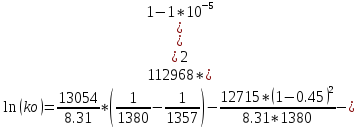
Ln(Х_b^s/ Х_b^l)=ln(ko) =-10.7

5. Расчёт и построение линий спинодалей в диапазоне темпертатур от 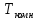до .

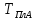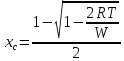
T, K	Xc1	Xc2
298	-0,090	0,989
300	-0,090	0,989
400	-0,117	0,985
500	-0,143	0,981
600	-0,168	0,977
700	-0,192	0,974
800	-0,215	0,970
900	-0,238	0,966
1000	-0,260	0,962
1100	-0,281	0,958
1200	-0,302	0,954
1685	-0,395	0,934

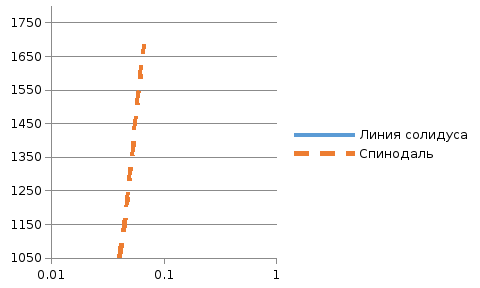
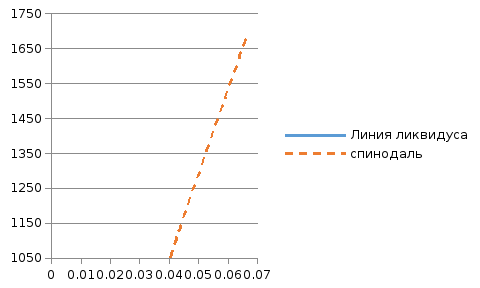
Рис. 6. Линии спинодалей в диапазоне темпертатур от 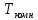до .

Вывод: в ходе работы были проанализированы диаграммы состояния и подобранные значения оптимальных параметров взаимодействия в твёрдом и жидком растворах, произведен расчет линии ликвидуса для модели идеального раствора и ее сравнения с экспериментальной. Можно сделать вывод, что для описания линии ликвидуса подходят модели квазирегулярного и регулярного раствора. Также расчёт и построение концентрационных зависимости активностей и коэффициентов активностей компонентов в твёрдом растворе 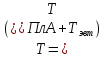при /2 в пределах области растворимости и в жидком растворе во всём диапазоне составов от х=0 до 1 при .
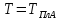