
Задачи нью
.pdf
Занятие 24
Тема: Уравнение Шредингера. Часть 2.
Цель: Потенциальная яма. Операторное представление физических величин. Средние значения физических величин. Гармонический осциллятор. Атом водорода.
Краткая теория
• Частица внутри одномерной бесконечно глубокой потенциальной ямы. Яма задает следующий вид потенциальной энергии U частицы:
U = 0 при 0 < x < l ,
U = ∞ для других значений координаты х.
Решение уравнения Шредингера позволяет найти собственные
функции частицы: |
ψ n |
= |
2 sin nπ x |
, |
а также соответствующие |
им |
|||||
|
|
|
|
|
|
|
l |
l |
|
|
|
энергии En |
= π |
2 |
! |
2 |
n 2 |
|
|
|
|
|
|
|
2 |
, где l - ширина ямы, m - масса частицы, n = 1, |
|||||||||
2, 3, … |
2ml |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
• Значения L, которые может принимать физическая величина, |
|||||||||||
описывающая |
некоторое |
|
свойство |
микрообъекта, находят |
из |
||||||
уравнения |
" |
= |
|
Lψ , |
в |
которое |
входит квантовый оператор |
||||
Lψ |
|
||||||||||
искомой величины. Каждой физической величине может быть сопоставлен свой оператор. Решением уравнения являются пары: волновые функции ψ 1, ψ 2, ψ 3, ... (собственные функции оператора) и
соответствующие им значения искомой физической величины L1, L2, L3, ... (собственные значения оператора).
Согласно принципу суперпозиции волновая функция произвольного состояния частицы может быть представлена в виде разложения по
собственным функциям: ψ = ∑ Cn ψ n , где в одномерном случае коэффициенты разложения Сn = ∫ψψ n*dx. В аспекте наблюдения каждое произведение CnCn* определяет вероятность получить значение Ln искомой физической величины при измерении.
•Среднее значение физической величины в состоянии,
характеризуемом волновой функцией ψ : |
|
= ∫ψ Lψ dx . |
|
||
L |
|
||||
• Запись |
операторов |
некоторых |
|
физических |
величин, |
характеризующих свойства частицы, имеет следующий вид. |
|
||||

Координата: |
" |
= x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
X |
|
|
|
|
$ ∂ |
|
$ ∂ |
|
|
$∂ |
|
||||||||||||
|
# |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Импульс: |
P |
= − |
i! |
|
, где |
= |
i |
|
+ |
|
j |
∂ |
+ |
|
|
k |
- дифференциальный |
||||||
векторный оператор «набла». |
|
|
|
∂ x |
|
|
|
y ∂ z |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Энергия: |
" |
|
! |
2 |
|
2 + U , где |
|
" |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
H |
= − |
|
|
H - |
оператор, который носит название |
||||||||||||||||||
2m |
|||||||||||||||||||||||
|
|
|
|
|
|
∂ 2 |
|
|
|
∂ |
|
|
∂ |
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
2 |
|
|
|
|||||||
«гамильтониан», |
|
|
|
= ∆ = |
|
+ |
|
|
+ |
|
|
∂ |
|
|
|
- |
оператор Лапласа, |
||||||
|
|
|
y2 |
|
z2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
∂ |
x2 |
|
|
∂ |
|
|
|
|
|||||||
представляющий сумму вторых частных производных по координатам от стоящей за ним функции, U - потенциальная энергия
частицы. В операторном виде стационарное уравнение Шредингера
"
может быть записано как Hψ = Eψ .
• |
Гармонический осциллятор. Потенциальная энергия частицы в |
||||||||
поле возвращающей силы F = − kx имеет вид U = |
kx2 |
= |
mω |
2 |
x2 , где ω |
||||
2 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
||
- |
циклическая |
частота колебаний. Возможные |
энергии |
|
частицы: |
||||
En = (n + |
1 |
)!ω |
, где n = 0, 1, 2, 3, …, даже при n = 0 частица обладает |
||||||
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
энергией, совершая так называемые «нуль-колебания». Собственная
функция |
основного состояния: |
ψ 0 = Aexp(− |
mω |
x2 ) , где А – |
|
2! |
|||||
|
|
|
|
постоянная, находимая из дополнительных условий.
• Атом водорода. Атом водорода содержит один протон и один электрон, находящийся в электрическом поле протона, что позволяет получить точное решение уравнения Шредингера и полностью описать состояния электрона. Представленное ниже решение получено в сферической системе координат, оно дает волновую функцию как произведений двух функций, первая из которых описывает зависимость от радиус-вектора r, вторая – угловую от полярного (отсчитывается от оси z) и азимутального углов θ и ϕ соответственно: ψ nlm = Rnl(r)Ylm(θ ,ϕ ), где R - радиальная часть, Y - шаровая гармоника, n, l, m - главное, азимутальное и магнитное квантовые числа соответственно. Волновая функция s-состояния, в
котором n = 1, l = 0, m = 0, имеет вид ψ |
100 |
= |
1 |
( |
1 |
) |
3 / 2 |
exp(− |
r |
) , где |
π |
a0 |
|
a0 |
|||||||
|
|
|
|
|
|
|
|
a0 |
= |
4πε |
0 |
! |
= 0,53 нм – первый боровский радиус, а r - расстояние от |
|
|
|
|
||||
e |
2 |
m |
||||
|
|
|
|
|||
ядра. Энергия электронного состояния с главным квантовым числом
n: |
En = − |
|
me4 |
. Следует особо отметить, что энергия не |
||||
32π |
2ε |
0 |
2 |
!2 n2 |
||||
|
|
|
||||||
зависит от квантовых чисел l и m. Такие состояния носят название «вырожденных».
Примеры решения задач
24-1. Частица находится в бесконечно глубокой потенциальной яме ширины l, расположенной вдоль оси х. Потенциальная энергия U частицы: U = 0 при 0 < x < l , U = ∞ для других координат. Найти волновую функцию и вероятность нахождения частицы в основном состоянии в малых областях пространства ∆ l = 0,01 l вблизи стенки и в средней части ямы.
• |
Запишем уравнение Шредингера |
2ψ + |
2m(E − U ) |
ψ |
= |
0 для частицы |
|||||
|
|
|
|||||||||
|
|
|
|
|
!2 |
|
|
|
|
|
|
в |
яме, учтя, что |
в пределах ямы |
U = |
0: |
∂ |
2ψ |
+ |
k 2ψ |
= 0 . Введено |
||
∂ |
2 |
||||||||||
|
|
|
|
|
|
x |
|
|
|||
обозначение k2 = |
2mE |
. Общее решение этого уравнения имеет вид: |
|||||||||
2 |
|||||||||||
|
|
! |
|
|
|
|
|
|
|
|
|
ψ |
= Asin(kx + α ) , где А и α - постоянные. Волновая функция должна |
||||||||||
удовлетворять условию непрерывности. Поскольку вне ямы частицы нет, то в этих областях пространства ψ = 0, что приводит к условию на границах ямы: ψ (0) = ψ (l) = 0.
Первое уравнение дает α = 0, из второго получаем Аsin(k l) = 0, откуда k l = ± nπ , где n = 1, 2, 3, … Постоянная А может быть найдена из условия нормировки волновой функции, достоверно находящейся в
яме: ∫l |
ψψ |
*dx = A2 ∫l |
sin 2 |
nπ x |
= |
1. После вычисления интеграла |
|
l |
|||||||
0 |
|
0 |
|
|
|
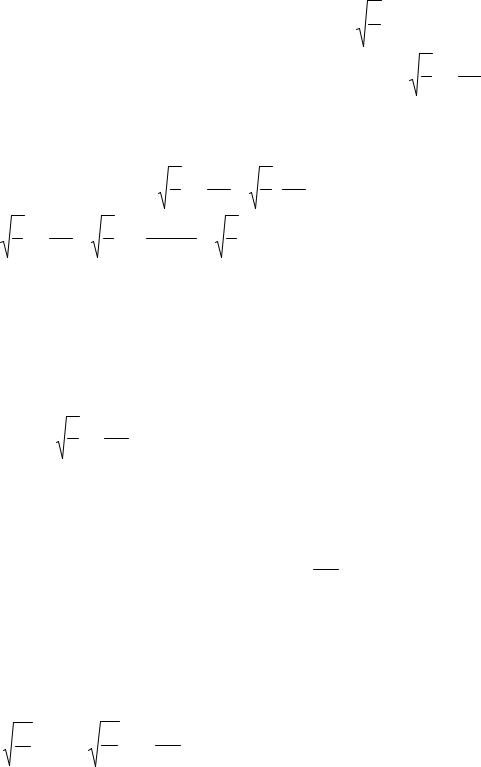
приходим к уравнению |
A2 |
l |
= |
1, откуда A = |
2 . |
Для основного |
||
|
||||||||
|
2 |
|
|
l |
|
|
|
|
(n = 1) состояния волновая функция принимает вид: ψ |
= |
2 sin π |
x . |
|||||
|
|
|
|
|
|
|
l |
l |
При расчете искомых вероятностей учтем малость заданного интервала 0,01l. Поскольку вблизи левого и правого краев ямы вероятности одинаковы, проведем рассмотрение только у левого края
х = 0. Для малых х: ψ |
= |
2 sin |
π |
x |
2 |
π |
x |
. В центре ямы для х l/2: |
|||||||||
|
|
|
|
|
|
|
|
|
l |
|
l |
|
l |
|
l |
|
|
ψ = |
2 |
sin |
π |
x |
|
2 |
sin |
π |
(l / 2) |
= |
|
2 |
|
|
|
|
|
l |
l |
|
l |
|
l |
|
l . |
|
|
Используем |
полученные |
||||||
приближения волновой функции для вычисления искомых вероятностей.
|
0,01l |
|
2 |
0,01l |
|
|
|
2 |
|
|
|||
У края ямы |
P1 = |
∫ψψ |
*dx = |
∫ |
(π x)2 dx = |
|
2π |
|
(0,01l)3 = 6,6 10− 6 . |
||||
|
l |
|
3 |
|
|||||||||
|
|
0 |
|
|
0 |
l |
|
|
|
3l |
|
|
|
|
|
|
(l+ |
0,01l ) / 2 |
|
2 |
(l+ |
0,01l ) / 2 |
|||||
Вблизи центра ямы P2 = |
|
∫ψψ |
*dx = |
|
∫1 |
dx = 0,02 . |
|||||||
|
l (l− |
||||||||||||
|
|
|
(l− |
0,01l) / 2 |
|
0,01l) / 2 |
|||||||
Ответ: ψ = |
2 sin |
π x |
, Р1 = 6,610-6, Р2 = 0,02. |
|
|
||||||||
|
l |
l |
|
|
|
|
|
|
|
|
|
|
|
24-2. Частица находится в одномерной бесконечно глубокой потенциальной яме шириной l. Потенциальная энергия U частицы: U = 0 при 0 < x < l , U = ∞ для других координат. Состояние частицы
описывает волновая функция ψ = Asin 2 π lx . Найти вероятность
пребывания частицы в основном состоянии, а также среднюю энергию в этом состоянии.
• Постоянную А находим из условия нормировки:
l |
|
|
|
l |
|
|
|
3x |
|
sin 2x |
|
sin 4x |
|
|
l0 = |
|
3l |
|
|
||
∫ |
ψψ |
* |
dx = A2 ∫sin4 xdx = A2 ( |
− |
+ |
) |
|
A2 |
= |
1, откуда |
|||||||||||
|
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
8 |
|
4 |
|
32 |
|
8 |
|
|||||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A = |
8 |
и ψ |
= |
8 |
sin 2 π |
x . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3l |
|
|
3l |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
||
Волновая функция ψ не является собственной функцией частицы в потенциальной яме, поэтому не описывает состояние с определенной энергией. Такое состояние следует рассматривать как суперпозицию
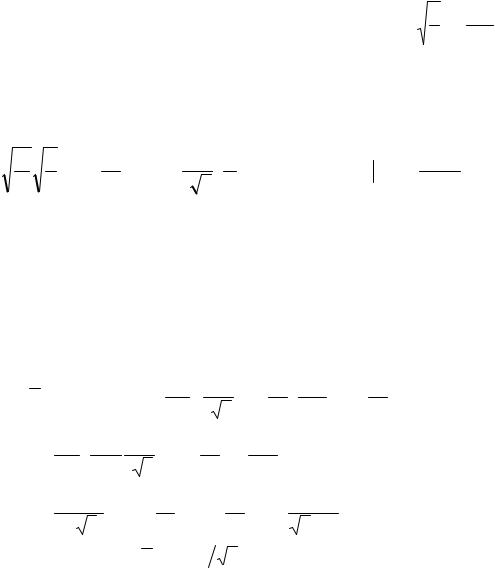
собственных состояний, входящих в существующее с некоторым весом. Функцию ψ можно представить в виде разложения
ψ = ∑ Cnψ n по собственным волновым функциям ψ n = |
2 sin nπ x . |
|
n |
l |
l |
Квадраты модулей коэффициентов разложения будут вероятностями Pn нахождения частицы в состояниях с соответствующими энергиями:
Pn = |
|
Cn |
|
|
2 = |
|
∫ψ |
n*ψ dx |
|
2 |
. Для n = 1 (основного состояния) получим: |
||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
2562 . |
P1 = |
( |
|
8 |
2 |
∫sin3 π x dx)2 = ( |
4 |
|
l (cos3 x − |
cos x))2 |
l0 )2 = |
|
||||||||||||
|
|
|
3l |
l |
0 |
l |
|
|
l |
3 |
π |
|
|
|
|
27π |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с волновой функцией ψ |
||||||
Среднюю |
энергию |
частицы |
в |
состоянии |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
находим |
согласно |
|
|
общему |
|
выражению: |
E = |
∫ψ *Hψ dx . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Гамильтониан частицы в потенциальной яме (U = 0):
Отсюда
l |
* " |
!2 |
l |
|
4 |
sin |
2 π x |
|
d 2 |
(sin |
2 π x |
|
E = ∫ψ |
Hψ dx = − |
2m |
∫ |
l |
3 |
l |
dx |
2 |
l |
|||
0 |
|
0 |
|
|
|
|
||||||
" |
!2 d 2 |
|||
H = − |
|
|
|
. |
2m |
dx2 |
|||
)dx = |
|
|
|
|
= |
− |
!2 |
2π |
2 2 |
4 |
|
∫l |
sin 2 π |
x cos 2π x dx |
= |
|
||||||
|
|
2m |
l |
l |
3 |
0 |
|
|
|
l |
|
l |
|
|
|
||
= |
− |
4!2π 2 |
l |
|
2 |
π x |
− |
sin |
4 π x |
)dx = |
π 2 !2 |
|
|||||
l |
3 |
3 |
∫(sin |
|
l |
|
l |
|
3ml |
2 |
|||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||
Ответ: P1 = 256/27π |
2 ; |
E = |
π |
|
2!2 |
|
3 ml2 |
|
|
|
|||||||
24-3. Считая |
известной |
|
волновую |
функцию |
основного состояния |
||||||||||||
гармонического осциллятора, определить энергию этого состояния Е0.
• |
Волновая |
функция имеет вид ψ = |
Aexp(− ax2 ) , где a = |
mω |
. |
|||||
|
||||||||||
|
|
|
|
|
|
|
ψ '= − 2Aaxexp(− ax2 ) |
2! |
|
|
Вычислим |
две |
первые |
производные |
и |
||||||
ψ |
''= − 2Aa(1− 2ax2 )exp(− ax2 ) , а затем подставим их в уравнение |
|||||||||
Шредингера: |
− |
2a + 4a2 x2 + |
|
2m |
(E0 − U ) = |
0 . Чтобы определить |
Е0, |
|||
|
2 |
|||||||||
|
|
|
|
! |
|
|
|
|
|
|

воспользуемся условием минимума потенциальной энергии частицы
U(0) = 0 при x = 0: |
− |
2a + |
2mE |
= |
0 |
|
E |
= |
a!2 |
= |
!ω |
|
|||
!2 |
, откуда |
m |
2 . |
||||||||||||
|
|
|
|
0 |
|
|
|||||||||
Ответ: E0 = |
!ω |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
24-4. В атоме водорода электрон находится в основном состоянии. Зная волновую функцию ψ 100 электрона, определить его среднее
расстояние до ядра. |
|
|
|
|
|
|
" |
|
|
• Уравнение Шредингера для атома водорода |
= Eψ включает в |
||||||||
Hψ |
|||||||||
|
" |
! |
2 |
|
e |
2 |
|
|
|
|
|
|
|
|
|
||||
себя гамильтониан вида |
H = − |
|
∆ + |
|
, в |
котором учтено |
|||
2m |
4πε 0 r |
||||||||
|
|
|
|
|
|||||
электрическое взаимодействие электрона и ядра - протона. Общее решение этого уравнения в сферических координатах более чем громоздко, поэтому воспользуемся частным случаем основного состояния: ψ 100 = C exp(− r / a0 ) , где С - постоянная, а0 – первый
боровский радиус. Постоянную С можно найти из условия нормировки по пространству, которое занимает электрон:
∫ψ 100ψ 1*00dV = 1. Интегрирование производится по пространству,
поэтому |
|
dV = |
|
4π r 2 dr - элемент объема в сферических координатах. |
||||||||
Подстановка |
|
|
|
волновой |
функции |
приводит |
к |
интегралу |
||||
∞ |
|
|
|
|
2r |
|
|
|
|
|
|
|
4π C2 ∫r2 exp(− |
|
)dr = |
1, который сводится к табличному интегралу |
|||||||||
|
|
|||||||||||
0 |
|
|
|
|
a0 |
|
|
|
|
|
||
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
вида ∫ xn exp(− x) = n! |
для n = 2. Решением полученного уравнения |
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
будет C |
= |
π |
1 |
|
. |
|
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Для определения среднего расстояния электрона до ядра необходимо
|
|
|
* " |
воспользоваться общей операцией усреднения: r = ∫ψ |
rψ dV . |
||
Учитывая, что волновая функция ψ 100 вещественна, а применение
оператора координаты к волновой функции дает простое умножение ее на координату, получим:
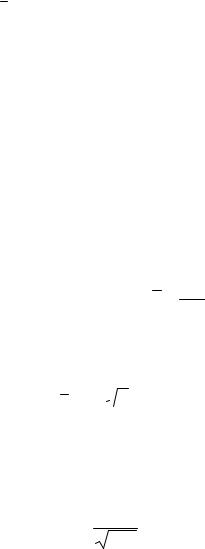
|
∞ |
∞ |
2r |
|
4 |
3! |
|
|
|
3a |
|
|
|
||
r |
= ∫ rψ 1200 4π |
r 2 dr = 4π ∫ r3 exp(− |
)dr = |
a0 |
4 |
= |
0 |
. |
Интеграл |
||||||
|
|
|
|
|
|
|
|||||||||
a0 |
3 |
2 |
4 |
|
4 |
|
|||||||||
0 |
0 |
|
a0 |
|
|
|
|
|
|
|
|||||
вычислен с помощью приведенного выше табличного интеграла для n = 3.
" |
= |
3a0 |
|
|
Ответ: r |
|
. |
||
4 |
||||
|
|
|
Задачи для самостоятельного решения
24-5. В одномерной бесконечно глубокой потенциальной яме шириной l находится частица в состоянии с волновой функцией ψ = Ax(l − x) . Определить вероятность ее пребывания в первом состоянии и соответствующую среднюю энергию.
Ответ: P1 = 960/π 6, E = 5!2 .
ml2
24-6. Вычислить средние значения координаты и квадрата координаты для частицы, находящейся в основном состоянии в бесконечно глубокой потенциальной яме шириной l.
Ответ: x = l /  2π , x2 = l2 /12 .
2π , x2 = l2 /12 .
24-7. Найти собственные функции и собственные значения оператора проекции момента импульса на ось z в сферических координатах.
Оператор имеет вид M z = |
|
− i! |
∂ |
, где ϕ |
- азимутальный угол. |
||||
|
∂ ϕ |
||||||||
|
|
|
|
|
|
|
|
|
|
Ответ: ψ |
= |
1 |
exp( im |
ϕ |
) , Mz = m!, где m = 0, 1, 2, … |
|
|||
2π |
|
||||||||
|
|
|
|
|
|
|
|
|
|
24-8. |
Определить |
|
возможные |
собственные |
значения |
||||
оператора проекции момента импульса Mz и их вероятности для
системы, находящейся в состоянии с волновой функцией ψ |
= Asin2 ϕ , |
где ϕ - азимутальный угол. (Необходимо разложить |
волновую |
функцию по собственным функциям оператора Мz, используя комплексное представление тригонометрических функций.)
Ответ: Mz = 0, ± 2 ! , P0 = 2/3 , P± 2 = 1/6.
24-9. В момент времени t = 0 волновая функция частицы имеет вид
ψ ( x ) = |
A exp( − |
x 2 / 2 a 2 − ik 0 x ) . Найти средние значения |
координаты и импульса частицы. |
||
Ответ: |
x = 0 , p = |
!k0 . |
24-10. Частица массой m находится в основном состоянии в потенциальном поле U(x) = k x2/2. Ее волновая функция
ψ = A exp( − α |
x 2 ) . Найти энергию частицы. |
|
Ответ: E = |
! |
k . |
|
2 |
m |
Контрольные задачи
24-11. Электрон находится на третьем уровне в бесконечно глубокой одномерной потенциальной яме. При переходе на первый уровень длина волны излучения составляет λ . Определить ширину ямы.
24-12. Определить собственные значения оператора Mz и их вероятности для системы, находящейся в состоянии с волновой функцией ψ = A(1+ sin ϕ ) , где ϕ - азимутальный угол.
24-13. Электрон в атоме водорода находится в основном состоянии. Найти средний квадрат расстояния электрона от ядра.
24-14. Вычислить средние значения координаты и квадрата координаты для основного состояния гармонического осциллятора.
