3. Каноническое распределение Гиббса

Пусть имеем замкнутую макроскопическую систему, энергия которой равна . Величина этой энергии является неизменной, то есть выполняется условие . Выделим в этой системе некоторую часть, значительно меньшую, чем сама система. Эту часть системы назовем подсистемой, а остальную часть системы назовем термостатом. Пусть подсистема находится в состоянии с энергией , а термостат в состоянии с энергией . Тогда для этих значений выполняется условие:

(3.1)

Условие (3.1) является точным при условии, что энергией взаимодействия подсистемы и термостата можно пренебречь.

Пусть энергии подсистемы соответствует состояний, а термостату с энергией соответствует состояний. Тогда в силу независимости подсистемы и термостата можно записать, что число состояний, в которых энергия подсистемы равна , а энергия термостата равна , определяется выражением:

(3.2)

Из определения вероятности следует, что вероятность того, что подсистема находится в состоянии с энергией , а термостат – в состоянии с энергией , пропорциональна числу состояний , то есть:

(3.3)

Из формулы (3.1) можно с достаточной степенью точности определить, что . Тогда формула (3.3) будет иметь вид:

(3.4)

В формуле (3.4) энергия много меньше энергии всей системы : . При этом условии число состояний термостата можно разложить в ряд по малому параметру . Но и при использовании формулы (3.4) и при разложении в ряд невозможно выполнить условие аддитивности, так как число состояний, как следует из (3.4) число состояний функция мультипликативная.

Чтобы выйти из этого затруднения будем использовать, связанное с числом состояний, понятие энтропии: , где - постоянная Больцмана. В нашем случае для числа состояний термостата имеем:

(3.5)

Из формулы (3.5) находим число состояний:

(3.6)

В последней формуле (3.6) энтропия , как и число состояний , является функцией и ее можно разложить в ряд по малому параметру :

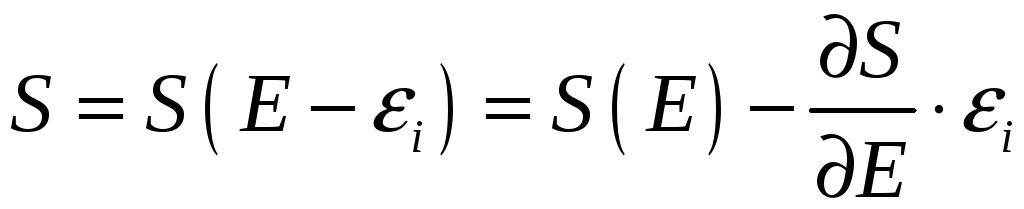(3.7)

В этом разложении пренебрегается членами второго порядка малости, что соответствует условию малости по сравнению с .

Из термодинамики известно, что 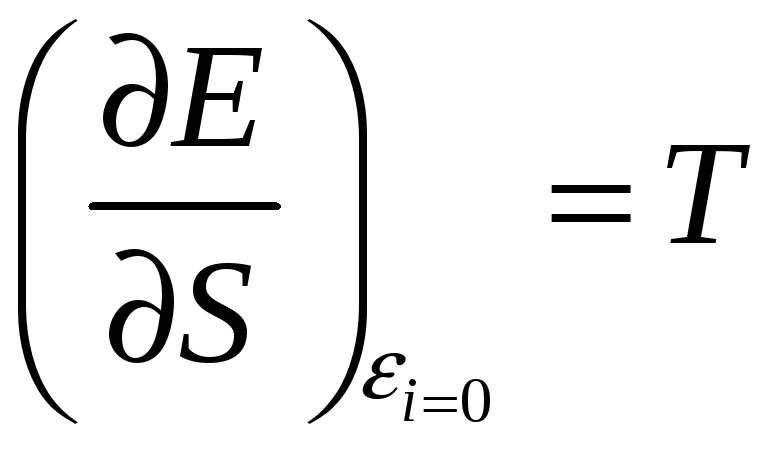(3.8). Здесь - статистическое определение температуры. При этих условиях и обозначениях число состояний термостата можно записать в виде:

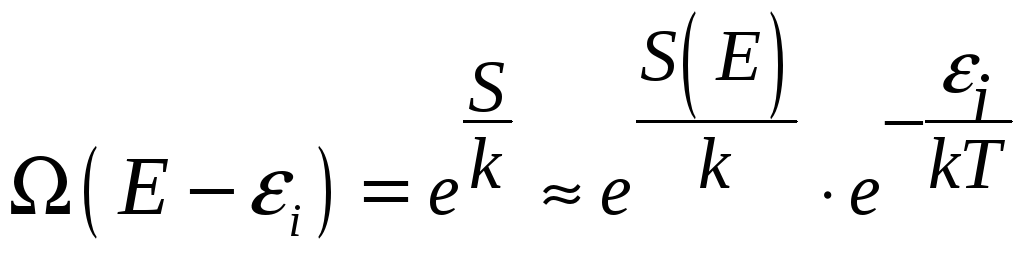(3.8)

Подставляем формулу (3.8) в формулу (3.4), тогда для вероятности состояния получаем:

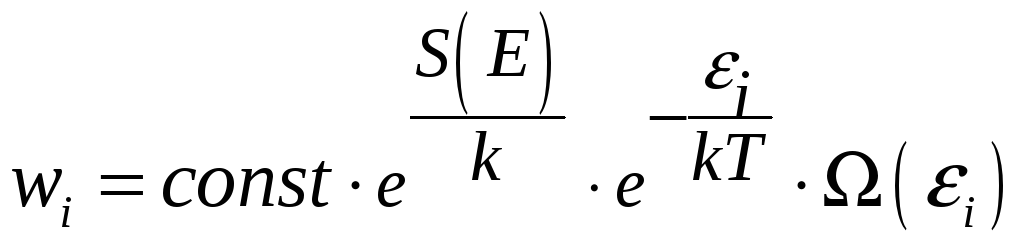(3.9)

Так как энергия всей макроскопической системы является величиной постоянной, то и величина является постоянной, не зависящей от свойств подсистемы. Ее можно включить в постоянную величину в формуле (3.9). Тогда получаем:

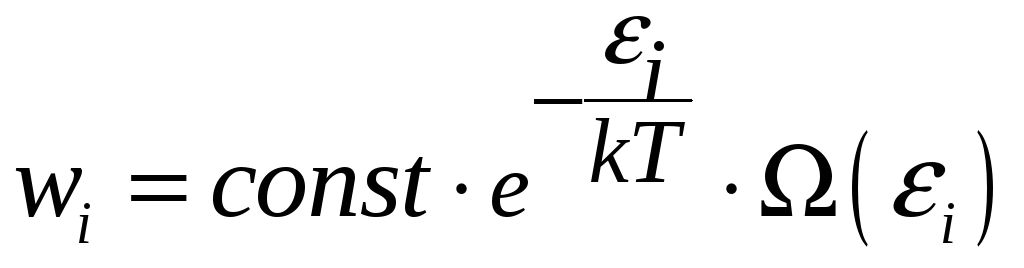(3.10)

Формула (3.10) представляет собой каноническое распределение Гиббса, которое показывает вероятность того, что некоторая подсистема находится в состоянии с энергией , а термостат - в состоянии с энергией .

Так как состояние термостата, в основном, интереса не вызывает, то обычно говорят, что формула (3.10) показывает вероятность того, что изучаемая подсистема находится в состоянии с энергией .

Чтобы использовать формулу (3.10) для решения практических задач, необходимо найти значение постоянной. Для решения этой задачи используем условие нормировки, согласно которому сумма вероятностей всех возможных состояний должна быть равна единице:

(3.11)

Подставляем формулу (3.10) в это условие:

.

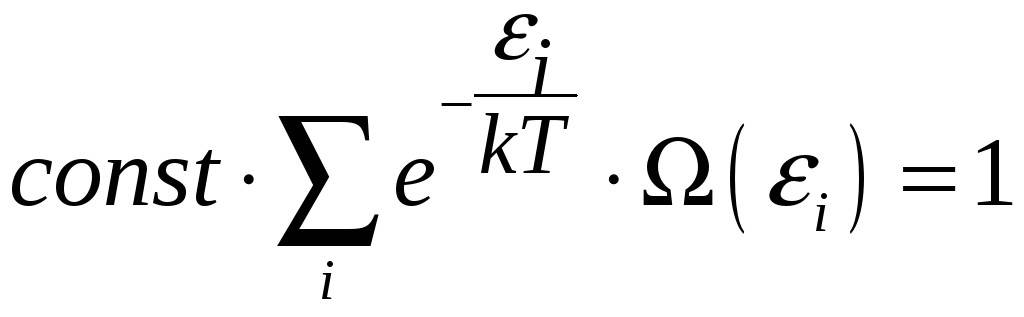Из этого выражения находим постоянную величину :

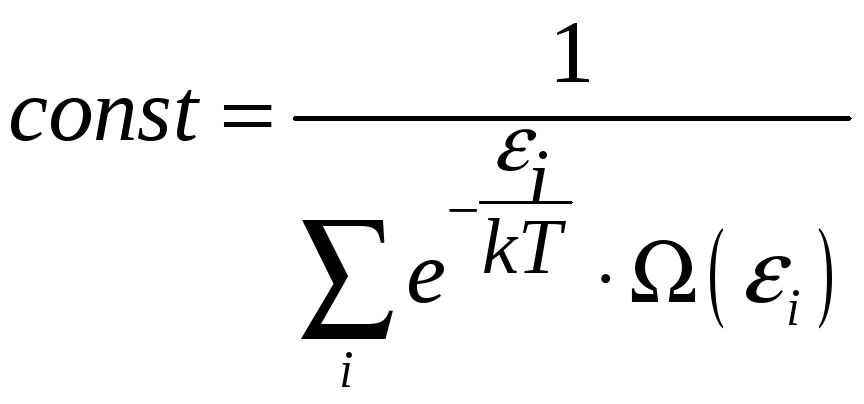(3.12)

Теперь можем записать каноническое распределение Гиббса, которое удобно применять при решении задач:

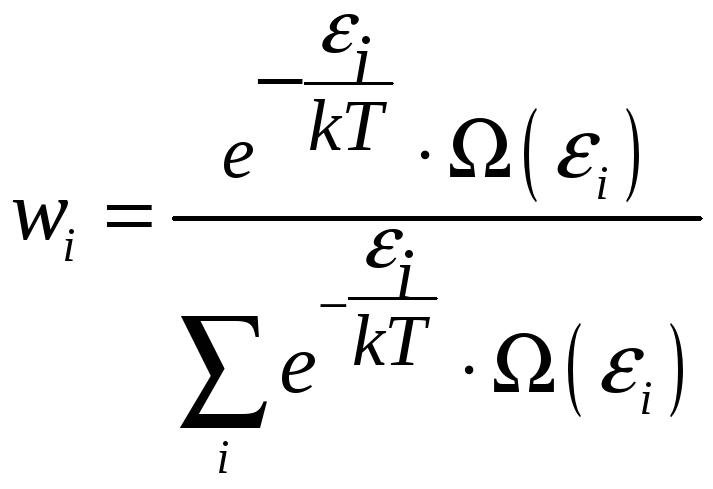(3.13)

Каноническое распределение Гиббса было сформулировано в 1901 году. Оно описывает распределение вероятностей состояний подсистемы, составляющей малую часть системы, находящейся в состоянии равновесия. При этом подсистема обменивается с оставшейся частью системы - термостатом – энергией.

Сумма в знаменателе формулы (3.13) играет в статистической физике важную роль. Ее называют статистической суммой:

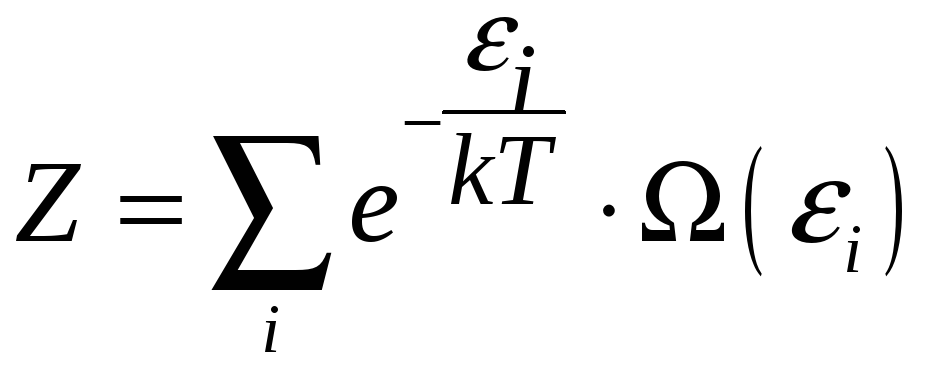(3.14)

Введение статистической суммы позволяет записать каноническое распределение Гиббса в виде:

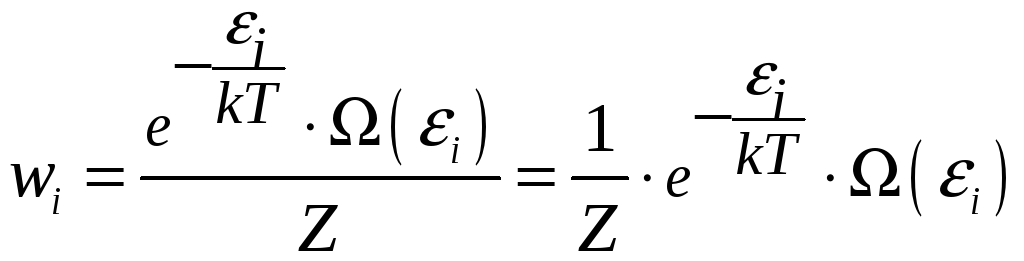(3.15)

Из формулы (3.15) следует, что каноническое распределение Гиббса для некоторой конкретной физической системы можно считать известным, если известны уровни энергии системы, то есть возможные значения и число состояний, соответствующее этой энергии, , которое представляет собой кратность вырождения этого уровня энергии.

Одной из особенностей канонического распределения Гиббса является то, что в нем не учитывается механизм взаимодействия изучаемой подсистемы с термостатом.

Значение канонического распределения Гиббса состоит в том, что оно позволяет вычислять средние значения любой величины, зависящей от состояния системы. Если - некоторая физическая величина, зависящая от энергии подсистемы , то по правилам определения среднего значения можно определить среднее значение этой величины: