
KMSF-Chast1-new
.pdf
Если оператор физической величины не зависит явно от времени, то
̂ |
|
1 |
|
|
|
= |
̂ ̂ |
(2.60) |
|
|
|
[ , ] |
Отсюда следует, что среднее значение производной оператора, коммутирующего с гамильтонианом, равно нулю. Такие величины называются сохраняющимися величинами. Очевидно, что сохраняющейся величиной является полная энергия системы, т.к. гамильтониан всегда коммутирует сам с собой. Поэтому, для того, чтобы среднее значение физической величины сохранялось, необходима коммутация квантового оператора этой величины с гамильтонианом.
Глава 3. Уравнение Шредингера в одном измерении
§3.1. Одномерная потенциальная яма с бесконечно высокими стенками
Рассмотрим один из простейших случаев движения частицы
когда одномерный потенциал |
|
|
0 |
0 x a |
|
U |
|
||||
|
|
|
|
x a, x 0 |
|
Стационарное уравнение Шредингера |
|
||||
|
|
2 |
|
|
|
|
|
U E |
|||
2m |
|||||
|
|
|
|||
для области внутри ямы принимает вид
вдоль оси x,
(3.1)
|
|
2 |
d |
2 |
x E . |
||
|
|
|
|
||||
2m dx |
2 |
||||||
|
|
||||||
|
|
|
|||||
Преобразуем уравнение (3.2) к виду:
d |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
k |
0. |
|
|
|
2 |
0 |
, |
2 |
|
dx |
2 |
k |
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
||
В (3.3) мы ввели волновое число k
k |
2 |
|
2mE |
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
(3.2)
(3.3)
(3.4)
Поскольку вне “ямы” потенциальная энергия равна бесконечности, можно ввести “естественные” граничные условия
23
0
Общее решение уравнения
a 0 .
(4.4) удобно представить в виде:
(3.5)
Asinkx Bcos kx
.
(3.6)
При x = 0 |
0 0 , |
|
откуда следует, что коэффициент В = 0. При x = а |
|||
a Asinka 0 |
, sinka 0 |
, |
ka n , n = 1,2,3,... (Для значения n=0 |
волновая |
||
функция тождественно обращается в ноль). |
|
|||||
Из (3.4) следует, что |
|
|
|
|
|
|
|
|
|
= |
2 2 2 |
|
(3.7) |
|
|
|
2 . |
|||
|
|
|
|
|
||
Мы получили условие квантования уровней энергии в потенциальной яме с бесконечными стенками, поскольку отличные от нуля решения имеются только для целых чисел n. Окончательно решение уравнения (3.3) имеет
вид
|
n |
|
A sin |
n |
|
a |
||
|
x
. Эти функции являются собственными функциями га-
мильтониана при данных граничных условиях. Постоянную А находим из
|
a |
x |
|
|
нормировки |
|
2 |
dx |
|
|
||||
|
|
|||
|
0 |
|
|
|
Замечание об импульсе.
|
|
a |
|
|
n |
|
|
1 |
|
|
|
|
2 |
|
|
2 |
2 |
|
|
||||
A |
|
sin |
|
|
|
x dx A |
|
|
1. |
Отсюда |
|
|
|
0 |
|
|
|
a |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Внутри ямы гамильтониан ˆ ˆp 2
H
2m
A 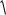 a2 .
a2 .
и казалось бы, что
мы имеем коммутатор оператора импульса с гамильтонианом равным нулю
ˆ |
|
ˆp |
|
|
ˆp,H ˆp, |
|
2 |
|
|
|
|
0 |
||
|
|
2m |
||
и получаем при этом, что энергия Е и импульс р одновре-
менно измеримы. Однако, это не так. Собственная волновая функция им-
пульса
|
|
ipx |
|
|
|
|
|
p |
C exp |
|
|
|
|
||
|
|
|
не удовлетворяет граничным условиям. Импульс
только по модулю имеемет постоянное значение, но сам импульс р не имеет определенного значения.
В окончательном виде собственные функции и энергии:
24
n x |
|
|
2 |
|
|
|
|
n |
|
|
||
|
|
|
|
sin |
|
x |
|
|||||
|
a |
|
|
|||||||||
|
|
|
|
|
|
a |
|
(3.8) |
||||
|
|
|
2 |
|
2 |
|
|
|
||||
E |
|
|
n2 |
|
|
|||||||
n |
2ma 2 |
|
|
|||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
Легко построить графики энергии, волновых функций и плотности вероятности для различных значений n. При n = 1 имеем низшее (основное) значе-
ние энергии частицы
|
|
|
|
|
|
|
|
2 |
|
2 |
|
E |
|
|
|
|
2 |
1 |
|
2ma |
|||
|
|
|
|||
.
En |
n(x) |
|
|
| n(x)|2 |
|
En |
|||||
n = 4 |
|
n = 4 |
|
|
|
|
|
|
|
|
|
n = 3 |
n = 3 |
n = 2 |
|
n = 2 |
|
n = 1 |
x |
n = 1 |
x |
0 |
a |
0 |
a |
Рис.3.1. Графики энергии, волновых функций и плотности вероятности для различных значений n.
Расстояния между соседними уровнями
|
|
|
|
|
|
|
|
2 |
|
2 |
2n 1 . |
|
|
|
|
|
|
|
|
|
|||
E |
n |
E |
n 1 |
E |
n |
|
2ma |
2 |
|||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
Оценим расстояние между уровнями для нескольких случаев:
(3.9)
1) Атомы или молекулы находятся в сосуде с размерами а ~ 1 см. Масса молекулы m ~ 10-23 г. Энергии квантованы, но расстояние между уровнями энергии
E |
|
~ |
3.14 2 1.05 2 1054 |
n ~ 1030 n |
эрг |
|
n |
|
|||||
|
1 |
10 23 |
|
|
||
|
|
|
|
|||
|
|
|
|
25 |
|
|

чрезвычайно мало. Для наших приборов они представляют практически сплошной спектр. Дискретность уровней никак не сказывается на движении молекул в таком сосуде;
2) В металле свободные или валентные электроны находятся в “потенциальной яме”, размеры которой пусть также порядка а ~ 1 см. Расстояния между уровнями при массе электронов m ~ 10-27 г равны
E |
|
~ 10 |
26 |
n эрг 10 |
14 |
n эВ |
n |
|
|
||||
|
|
|
|
|
|
и дискретность уровней по-прежнему не сказывается на движении электронов в металле;
3) Для электронов, находящихся в яме с размерами порядка размеров атома а ~ 10-8 см, расстояние между уровнями весьма существенно
E |
|
~ 10 |
10 |
n эрг 10 |
2 |
n эВ . |
n |
|
|
||||
|
|
|
|
|
|
Рассмотрим теперь 3-х мерную прямоугольную яму с бесконечными стенками. Пусть размеры ямы равны: a, b, c. Внутри ямы потенциальная энергия равна нулю: U = 0 при 0 x a, 0 y b, 0 z c. На границах U = . Движение частицы в яме происходит независимо вдоль осей x, y и z. Тогда волновая функция может быть представлена в виде произведения функций
|
|
|
|
|
8 |
|
sin |
n1 |
x sin |
n2 |
y sin |
n3 |
z |
|
|
|
|
|
|
|
|||||||
n n n |
|
|
abc |
|
a |
|
b |
|
c |
||||
1 |
2 |
3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
При этом энергия равна сумме энергий движений по всем трем осям:
|
|
|
|
|
|
n |
2 |
|
n |
2 |
|
n |
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||
En n n |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
при |
n1, n2, n3 = 1, 2, 3, .... |
|
1 2 |
3 |
|
2m |
|
|
2 |
|
b |
2 |
|
c |
2 |
|
|
|
||
|
|
|
a |
|
|
|
|
|
|
|
|
||||||
(3.10)
(3.11)
Когда размеры ямы: a, b, c соизмеримы, либо a = b (b = c), либо a = b = c возникают вырожденные уровни энергии, когда одному и тому же значению энергии соответствуют несколько состояний, описываемых различными функциями.
§3.2. Одномерная потенциальная яма с конечными стенками
26
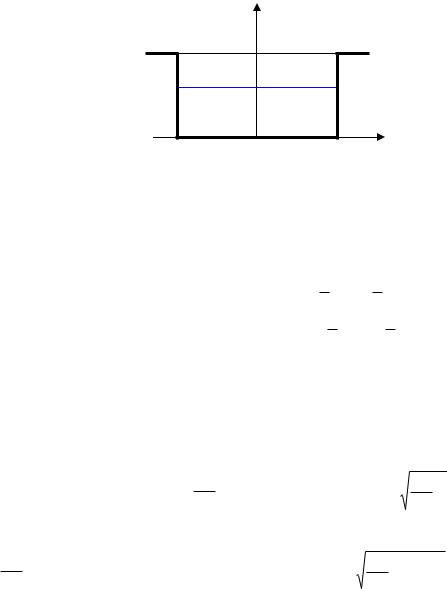
Рассмотрим одномерную прямоугольную яму со стенками конечной высоты.
U0
E
x
-a0/2 |
0 |
a0/2 |
Рис.3.2. Одномерная прямоугольная яма со стенками конечной высоты.
Выберем начало координат на дне ямы симметрично относительно стенок:
|
0 , |
|
a |
x |
a |
|
||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
U x |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
, |
x |
a |
; x |
a |
||
|
|
|
||||||
U |
0 |
|
|
|||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||
(3.12)
Найдем сначала решения уравнения Шредингера внутри и вне ямы. Для получения общего решения необходимо “сшить” эти решения на границе ямы. При энергии частицы E > U0 имеем непрерывный спектр энергий, частица пролетает над ямой и может иметь любую энергию. В самом деле, внутри
ямы имеем уравнение
шение в этой области
|
2m |
E 0. |
||
|
2 |
|||
|
|
|||
|
|
|
||
x A cosk x |
|
1 |
0 |
Вводя
B sin k x. |
|
1 |
0 |
k |
|
|
2m |
E , записываем ре- |
|
|
|
||||
0 |
|
2 |
|||
|
|
|
|
||
|
|
|
|
|
|
Вне ямы имеем уравнение
|
2m |
E U |
|
|
||
|
2 |
0 |
||||
|
|
|
||||
|
|
|
|
|
||
ние вне ямы |
|
x |
||||
чаем, что любые ной спектр при E
0. |
Вводя волновое число k0 |
2m |
E U 0 |
, получаем реше- |
|||
|
2 |
||||||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
Acos k0 x B sink0 x |
. Сшивая эти решения на границе, полу- |
||||||
энергии частицы разрешены. Таким образом, имеем сплош-
> U0.
Рассмотрим подробнее случай, когда энергия частицы E < U0. В этом случае мы получаем дискретный спектр связанных состояний. Для двух областей:
|
|
|
2 |
2 |
|
2mE |
|
|
|||
|x| < a/2 |
|
k 0, |
k |
|
|
|
|
, |
(3.13) |
||
|
2 |
||||||||||
|
|
||||||||||
|x| > a/2 |
2 0, |
2 |
|
2m |
|
U 0 E 2 k 2 . |
(3.14) |
||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
27 |
|
|
|
|||
Введем оператор четности с помощью соотношения |
ˆ |
P x x . |
Собственные числа оператора четности могут быть получены, если повторно подействовать им на исходную волновую функцию. Тогда получаем, что
ˆ ˆ |
2 |
|
|
PP x x x . Таким образом, значения собственных чисел = 1. |
|||
Для значения = 1, получаем |
“четное” состояние, а для = -1, имеем “не- |
||
четное” состояние. Поскольку |
U x U x |
, то оператор четности коммутиру- |
|
|
|||
ет с гамильтонианом рассматриваемой задачи
ˆ ˆ P,H
0
.
(3.15)
Из (3.15) следует, что все собственные функции гамильтониана имеют определенную четность. Рассмотрим эти состояния поочередно.
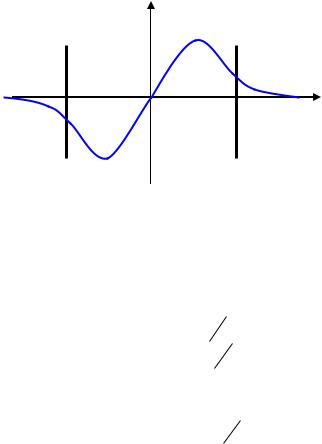
Нечетные состояния. Запишем решения уравнений (3.13) и (3.14) для
нечетных состояний
|
0 |
-а/2 |
а/2 |
Рис.3.3. Схематический вид нечетной волновой функции в прямоугольной яме
конечной глубины.
|
|
A sin kx |
|
|
|
|
|
|
|
|
|
|
C exp x , |
x a |
|
|
|
|
2 |
|
|
|||
|
x a |
|||
|
|
C exp x , |
||
|
|
|
|
2 |
(3.16)
На Рис.3.3. показано, что частица проникает вне области ямы, при этом глубина проникновения частицы под барьер L ~ 1 .
Из условий непрерывности волновой функции и её производной на границе x = a/2 следует:
28
|
Asin |
ka |
|
|
a |
, |
||
|
|
C exp |
|
|
|
|||
|
|
2 |
|
|
|
2 |
|
|
|
|
ka |
|
|
|
a |
||
kAcos |
|
|
||||||
|
C exp |
|
. |
|||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|||||
(3.17)
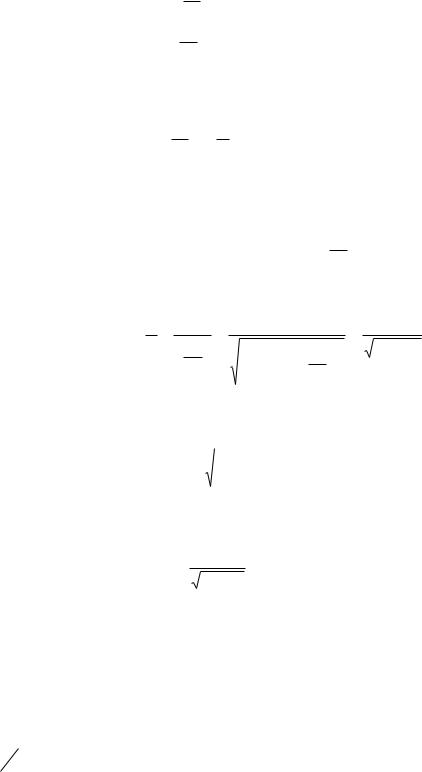
Делением верхнего уравнения на нижнее уравнение получаем, что
tg |
ka |
|
k |
. |
|
2 |
|
||||
|
|
|
(3.18)
Это трансцендентное уравнение определяет энергии разрешенных состояний. То же самое уравнение получим в силу симметрии из граничного усло-
вия при x = -a/2. Введем обозначение
t
ka 2
, тогда для правой части (3.18)
получаем
k |
|
|
t |
|
|
|
|
|
t |
|
|
|
|
|
t |
|
|
a |
|
|
2 |
|
|
|
2 |
2 |
|
2 |
|||||
|
|
a |
ka |
|
t |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
,
где введен параметр мощности ямы:
|
a |
|
|
mU 0 |
|
. |
|
|
2 |
||||||
|
|
|
|||||
Для определения спектра надо решить трансцендентное уравнение
tgt |
|
t |
|
. |
2 |
|
t |
||
|
|
2 |
||
|
|
|
(3.19)
(3.20)
Рассмотрим решение этого уравнения графически, для чего построим отдельно правую и левую части уравнения. Точки пересечения дают корни этого уравнения. Из рисунка видно, что решения имеются не при всех . Чем больше мощность ямы , тем больше корней уравнения - больше уровней энергии. При уменьшении число корней уменьшается. А при мощности
|
|
2 |
, т.е. при |
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
mU |
a |
2 |
2 |
|
|
2 |
|
|
|
||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
0 |
|
|
|
4 |
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
||||
,
29
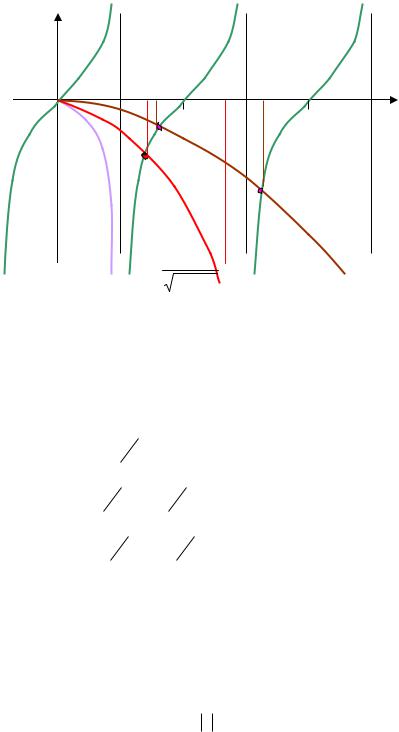
корней соответствующих нечетным состояниям нет вовсе. Напомним, что t0 = 0 и E0 = 0 не являются корнями, т.к. при этом решение внутри ямы естьAx , которое не удовлетворяет граничным условиям.
tgt
/2 |
|
3 /2 |
2 |
t |
|
|
|
|
|
|
|
t |
|
|
2 |
t |
2 |
||
|
||||
|
|
Рис.3.4. Графическое нахождение собственных энергий нечетных состояний.
Итак, для нечетных состояний,
- при мощности ямы |
|
|
2 |
||
|
получаем:
нет дискретных состояний;
-при мощности ямы
-при мощности ямы
т.д.
|
|
3 |
|
2 |
2 |
||
|
3 2 5 2
существует 1 нечетное состояние;
существует 2 нечетных состояний и
Четные состояния. Запишем теперь решения для четных состояний:
|
|
|
B cos kx |
|
|
|
D exp x |
||
|
|
|||
|
|
|
|
|
На границе ямы при x = a/2 имеем:
(3.21)
30
|
|
ka |
|
|
a |
|
|
|
||
|
B cos |
|
|
|
|
|
, |
|
|
|
|
|
D exp |
|
|
|
|
|
|||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
ka |
|
|
|
|
a |
|
||
kBsin |
|
|
|
. |
||||||
|
D exp |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|||||
(3.22)
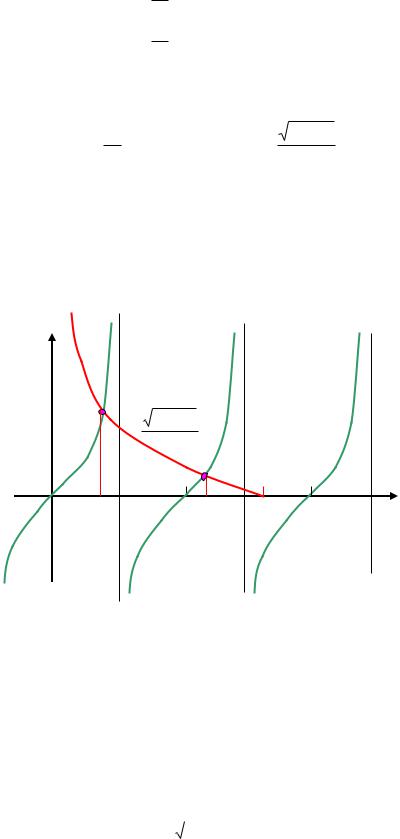
Откуда получаем новое трансцендентное уравнение
|
ka |
|
|
|
|
|
2 |
t |
2 |
tg |
|
или |
tgt |
|
|
||||
2 |
k |
|
|
t |
|
||||
|
|
|
|
|
|
|
.
(3.23)
В силу симметрии то же уравнение дают граничные условия при x = -a/2. Из графического решения этого уравнения видно, что при всех возможных значениях параметра хоть одно решение есть всегда. Чем больше , тем больше четных решений.
|
|
|
|
|
tgt |
|
|
|
|
2 |
t |
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
/2 |
|
|
3 /2 |
2 |
t |
|
Рис.3.4. Графическое нахождение собственных энергий четных состояний.
Итак, при мощности ямы получаем одно четное решение, при мощности2 получаем два четных решения и т.д.
Рассмотрим теперь “мелкую” яму, для которой << 1. Для такой ямы достаточно легко найти энергию единственного четного состояния (t << 1).
|
tgt t |
|
2 |
t 2 |
|
|
Из (3.23) следует, что |
|
|
|
|
. Решая это уравнение, получаем |
|
|
|
|
|
|||
|
|
|
|
t |
||
31
t |
2 |
|
2 |
t |
4 |
|
2 |
|
4 |
. |
|
|
|
|
|
|
Вспоминая, что
t |
ka |
|
2 |
||
|
и
|
a |
mU |
0 |
|
|
|
|
|
|
2 |
|
, записываем для
квадрата волнового числа
k |
2 |
|
4 |
t |
2 |
|
4 |
a |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
a |
2 |
|
|
|
a |
2 |
|
|
|
|
|
|
|
|
|
|||
2 |
mU |
|
|
|
a |
|
|
|
|||
2 |
|
0 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
mU |
|
|
|
2mU |
|
|
|
a |
|
|
|
|
|
|
||||||
2 |
|
0 |
|
|
2 |
0 |
1 |
|
||
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
2 |
mU |
|
|
|
|
|
|
2 |
|
0 |
, |
2 |
|
|
|
|
|
|
а для энергии
|
2 |
k |
2 |
|
|
2 |
2m |
|
|
|
ma |
2 |
|
|
|
|
|
|
ma |
2 |
|
|
|
|||
E |
|
|
|
|
U |
|
|
U |
|
U |
|
|
U |
|
||||||||||||
|
|
|
|
|
|
2 |
1 |
|
2 |
0 |
|
1 |
|
2 |
0 |
. |
||||||||||
|
2m |
|
2m |
0 |
|
|
2 |
|
|
0 |
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Первый (четный) уровень энергии находится теперь у самого
(3.24)
“верха” ямы.
В одномерной яме с конечными стенками всегда существует хотя бы одно связанное состояние. При малой глубине и ширине (мощности) ямы в яме имеется только один четный уровень. С ростом U0 и a растет мощность ямы,
и появляются новые уровни при прохождении параметром значений
2
n
,
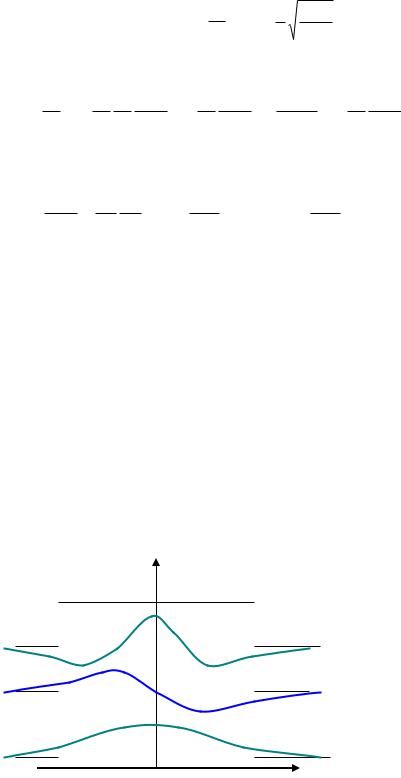
где n – целое число. Четные и нечетные уровни появляются по очереди, причем вначале четные. Качественное поведение волновых функции низших состояний показано на Рис.3.5. Возводя в квадрат эти волновые функции, получаем плотность вероятности нахождения частицы при данной координате.
|
|
|
|
U0 |
|
|
|
n=3 |
|
|
3 |
|
E3 |
||
|
|
|
|
|
|
||
|
|
|
|
2 |
|
E2 |
|
n=2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
E1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-a0/2 |
0 |
a0/2 x |
||||
Рис.3.5. Качественное поведение волновых функции низших состояний.
32
