Добавил:

arthurer Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Квантовая механика и статистическая физика

Файл:

KMSF-Chast1-new

.pdf

Скачиваний:

Добавлен:

08.02.2019

Размер:

1.91 Mб

Скачать

☆

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

Уравнение для координатной части волновой функции

	2					,
		2					(2.15)
2m		r	U r	r	E r

или

ˆ				(2.16)
H r		E r

называется стационарным уравнением Шредингера.

Полная волновая функция стационарного состояния имеет вид

				i	Et
					Et	(2.17)
			r ,t e		r ,	(2.17)

где (r) – решение стационарного уравнения Шредингера.						Плотность веро-
ятности распределения		2	не зависит от времени, т.е. стационарна.
ятности распределения	r ,t		не зависит от времени, т.е. стационарна.

§2.2. Операторы

Операторный метод - традиционная и основная формулировка квантовой механики. В квантовой механике любой динамической переменной, любой физической величине приводится в соответствие квантово-механический оператор.

Оператор	ˆ	- это правило, по которому любой
	F

водится в соответствие другая функция f:

выбранной функции при-

ˆ	(2.18)
f F

Ранее мы уже встречались с операторами:	,	, rot ,... , div ,... . При
	2

использовании операторов имеется договорное условие: оператор пишется всегда слева от функции, которая стоит справа от него и оператор действует на все, что стоит справа от него (если нет ограничивающих скобок).

В квантовой механике применяются только линейные операторы, чтобы не нарушался принцип суперпозиции состояний. Свойство линейных операторов:

ˆ	ˆ	ˆ	,	(2.19)
F C1 1	C2 2 C1F 1	C2 F 2	,	(2.19)

где С1, С2 - произвольные постоянные.

Основные операторы квантовой механики в координатном представлении:

1)Оператор координаты: xˆ x является оператором умножения;

2)Оператор полной энергии (гамильтониан)

ˆ			2
ˆ				2				(2.20)
H					U r			(2.20)
		2m
является суммой операторов кинетической
ˆ					2
ˆ							2	(2.21)
E	kin							(2.21)
	kin		2m
			2m
и потенциальной энергии
		ˆ				;		(2.22)
	U		U r			;		(2.22)
3) Оператор импульса. Исходя					из		выражения для кинетической	энергии

E	kin

p	2
p		, получим, что оператор импульса равен
2m		, получим, что оператор импульса равен
2m		ˆ
		ˆ
			(2.23)
		p i .	(2.23)

Оператор проекции импульса на ось x

pˆ		i		.	(2.24)
pˆ	x	i	x	.	(2.24)
	x

4) Оператор момента импульса

̂ = ̂ × ̂ = |

−

Действия с операторами: 1) Суперпозиция

∂

∂x

−

∂

∂y

−

∂ \| .		(2.25)
∂z

ˆ			ˆ	ˆ	(2.26)
G C C C G C G ;					(2.26)
1	2		1	2
2) Сумма операторов
ˆ	ˆ	ˆ	ˆ		(2.27)
G F G F ;					(2.27)
		14

3) Произведение операторов
̂ ̂		̂	̂		(2.28)
( )Ψ = ( );					(2.28)
ˆ	ˆ	некоммутативны, т.е. их последовательное
Вообще говоря, операторы G и	F	некоммутативны, т.е. их последовательное
				ˆ ˆ	ˆ ˆ
действие не совпадает с последовательным обратным действием: GF FG .
Можно определить коммутатор двух операторов
ˆ	ˆ	ˆ ˆ		ˆ ˆ	(2.29)
G, F GF FG					(2.29)
и антикоммутатор
	ˆ	ˆ	ˆ ˆ	ˆ ˆ	(2.30)
F,G FG GF .					(2.30)

Если для двух операторов выполняется условие

ˆ ˆ	ˆ ˆ
GF FG ,

(2.31)

т.е. их коммутатор равен нулю, то говорят, что эти операторы коммутируют. Для того, чтобы найти коммутатор, надо подействовать им на произвольную

функцию Ψ( ). Например, не коммутируют операторы ̂ и ̂, коммутатор

которых равен:

x i x

i ,

i x

xˆ, pˆ	x	i .	(2.32)
	x

Очевидно, что операторы yˆ и

pˆ	x

коммутируют,

т.е.

yˆ,

pˆ	x
	x

Собственные функции и собственные значения

В квантовой механике каждой физической величине сопоставляется оператор. Рассмотрим задачу определения собственных чисел f и g, и собствен-

ных функций и операторов		ˆ		ˆ
ных функций и операторов		F		и G :
		F
ˆ	f n n
F n	f n n		,	(2.33)
ˆ	gn n		,	(2.33)
ˆ
G n

где n - значок, соответствующий номеру решения. Собственные функции -

это такие функции, которые под действием оператора G переходят сами в себя, умноженные на постоянное число gn. Соответствующие значения gn

называются собственными значениями оператора ˆ Собственные волно-

G .

вые функции описывают в квантовой механике такие состояния, в которых

данная физическая величина g имеет определенное значение gn. Иначе гово-

ря, если частица (или система) находится в состоянии

n , то ее физическая

величина g в этом состоянии равна gn и постоянна. Совокупность собствен-

	ˆ
ных значений gn называется спектром оператора	G	.
ных значений gn называется спектром оператора		.

Спектр собственных значений может быть дискретным и непрерывным. Дис-

	ˆ		g
кретный спектр gn имеет место, если уравнение	G	n		n	n	имеет решение

не при всех, а только при определенных gn. Непрерывный или сплошной спектр gn имеет место, когда это уравнение имеет решение при всех значениях gn или хотя бы при всех gn в некоторой области. Спектр собственных значений может быть смешанным, т.е. состоящим из дискретных и непрерывных значений gn. Уравнение на собственные значения оператора координаты xˆ x в координатном представлении квантовой механики имеет решение при всех значениях координаты, т.е. x имеет сплошной спектр. Собственные функции

	i	p x
оператора проекции импульса Ae		p x
оператора проекции импульса Ae		x
		x

существуют при любых значениях px, имеет непрерывный спектр.

находятся из

т.е. оператор

i		p
	x

проекции

	. Решения
x	. Решения
импульса		px
		ˆ

Решения стационарного уравнения Шредингера ˆ зависят от вида H n En n

оператора потенциальной энергии . При этом можно получить как дис- U r

кретный спектр (электрон в атоме водорода), так и непрерывный спектр (свободная частица).

§2.3. Самосопряженные (эрмитовы) операторы и их свойства

Непосредственно измеряемые (“наблюдаемые”) физические величины ве-

щественны, т.е. все собственные значения оператора ˆ - { g } должны быть

G n

вещественны. В результате измерения физической величины, описываемой

оператором ˆ получаем:

G ,

1) если физическая система (частица) находится в состоянии, описываемом собственной функцией n , то при измерении получим соответствующее собственное значение gn ;

2) если система (частица) описывается произвольной функцией , то при

измерении наблюдаемой, т.е. действии оператора ˆ , получим линейную

комбинацию из собственных значений gn - некое среднее значение, которое тоже вещественно.

Введем понятие транспонированного оператора					ˆ	т р	, который определя-
Введем понятие транспонированного оператора					F		, который определя-
ется из соотношения	2 dV F
1 F	2 dV F		1	2 dV ,			(2.34)
* ˆ	ˆ	тр	*

т.е. транспонированный оператор дает тот же результат, действуя на левую

функцию, что и оператор		ˆ
функцию, что и оператор		F , действуя на правую.
Самосопряженные операторы определяются следующим равенством
	* ˆ			ˆ	*	ˆ	*
	* ˆ	2 dV	2	ˆ	dV 2	ˆ	dV ,	(2.35)
	1 F	2 dV	2	F 1	dV 2	F 1	dV ,	(2.35)
ˆ					ˆ
где F	- оператор, сопряженный к оператору F .
Если
		ˆ		ˆ
		F		F ,				(2.36)
								(2.36)

то этот оператор называется эрмитовым или самосопряженным операто-

ром. Можно сказать, что действие оператора	ˆ	на правую от него функцию
	F

совпадает с действием комплексно сопряженного оператора на левую функцию:

* ˆ	ˆ	*	ˆ *
		dV		*	(2.37)
1 F 2 dV	2 F 1		2 F	1 dV .

Таким образом, сопряженный оператор – это комплексно сопряженный оператор от транспонированного оператора

ˆ	ˆ	тр	*
ˆ	ˆ	тр	.			(2.38)
F	F		.			(2.38)
				ˆ	d
Рассмотрим оператор дифференцирования				F	dx	. Будем считать, что

волновые функции равны нулю на бесконечности. Вычислим оператор, со-

пряженный оператору

с помощью интегрирования по частям:

dx 0

dx.

Таким образом, оператор, сопряженный оператору

ˆ F

d dx

, равен

ˆ			d

F			dx

и, следовательно, оператор

не является эрмитовым. Очевидно, что

ˆp

оператор импульса

F i

x - самосопряженный оператор.

dx .

x 1

Оператор координаты Рассмотрим уравнения

xˆ x

ˆ F n

также

		n
n		n

эрмитов оператор.

и	ˆ * *	* *	,	откуда
	F n	n n

	* ˆ			ˆ	*
n		2	dV n			*
	n F n dV n n			F n		dV n .

(2.39)

Данное равенство означает, что собственные значения эрмитова оператора вещественны.

Произведение двух эрмитовых коммутирующих операторов есть эрмитов оператор

ˆ ˆ	ˆ ˆ	ˆ ˆ	ˆ ˆ	(2.40)
FG F G		GF	FG .	(2.40)

Пусть мы имеем дискретный набор собственных значений и собственных

функций эрмитова оператора ˆ (причем считаем, что нет вырождения, т.е.

все волновые функции n разные для разных собственных значений n ):

1 , 2 , 3 ,...

В математике строго доказано, что набор собственных волновых функций эрмитова оператора образует полную систему ортонормированных волновых функций, т.е.

*		m n
	0,	m n
m n dV		m n	mn .	(2.41)
	1,	m n

В самом деле, для доказательства ортогональности рассмотрим два равенства

F
	ˆ	n	n	n		(2.42)

	ˆ
	F	m			m
			m

Умножим слева первое уравнение на Вычитая второе уравнение из первого

	m , получаем:
тов оператор) m	m , получаем:
	0 n


m	,		второе на		n , и проинтегрируем.
m	,		второе на		n , и проинтегрируем.
					ˆ
уравнения и учитывая, что ( F - эрми-
			dV
			dV	,
m		m	n	,
m		m	n

				dV 0 .	(2.43)
n	m		n
		m

Отсюда следует, что если n m, то			n dV 0	. Полнота набора означает,
		m

что любую функцию можно разложить в ряд по функциям n .

В случае, когда имеем вырождение, волновая функция берется в виде линей-

ной комбинации	n	n	n	n	n	n	n	..., где все волновые функции
		1	1	2	2	3	3

имеют одно и то же собственное значение

ˆ
F	n
	i

		n
n		n
		i

. При этом линейные

комбинации можно сделать такими, что новые волновые функции будут ортонормированными.

Рассмотрим разложение произвольной функции в ряд по системе собственных функций самосопряженного линейного оператора

		.
r	Cn n r	.	(2.44)

Коэффициенты разложения можно получить, умножив обе части выражения

на

и интегрируя:

dV Cn kn

k r dV Cn n

k r

Cn k r

Ck .

(2.45)

Таким образом,

dV .

C k r

k* r

(2.46)

Квадрат коэффициента			k
		C	2
		C
	, присутствует
ваемом r	, присутствует

дает вероятность того, что в состоянии, описыпримесь состояния k .

Если имеем непрерывный спектр значений, тогда волновую функцию раскладываем в интеграл


r	C r	d ,	(2.47)

где коэффициенты определяются

C				1

1

		dV .	(2.48)
r	r

Волновые функции непрерывного спектра нормируются на - функцию

			dV ' .
'	r	r	dV ' .	(2.49)

Свойства - функции.

Функция обращается в

x a	везде равна нулю за исключением точки x = a, где она

бесконечность:

0,	x a
x a	x a
,	x a

или

0,	x 0
x	x 0
,	x 0

(2.50)

		Интеграл от - функции равен единице (беско-
	-функция	нечность с мощностью равной 1):

		x a dx 1	или x dx 1 .	(2.51)

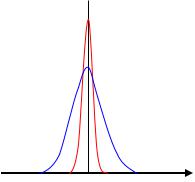
		Геометрически -функцию можно рассматри-
		вать как предел максимума, стремящегося к
a	x	бесконечности в точке a и сохраняющего пло-
		бесконечности в точке a и сохраняющего пло-

щадь под кривой равной единице. Важное свойство - функции состоит в том, что она “вырезает” из функции в подынтегральном выражении значение этой функции в точке a


x x a dx a .	(2.52)

Последнее условие и нормировка позволяет получать коэффициенты C .

§2.4. Вычисление средних значений. Обозначения Дирака
Поскольку вероятность найти частицу в элементе объема dV равна
*
dW	r	r dV , то можно определить средние значения различных физиче-

ских величин. Напомним, что среднее значение, например координаты, определяется выражением

xdW x xdx ,

(2.53)

где вероятность значения dW определяется dW x dx . Аналогично получаем для средних янии, определяемой волновой функцией x ,

через плотность вероятности значений координаты в состо-

	x x x dx

x		x x dx	.	(2.54)

Если волновая функция наты равно

уже нормирована, то среднее значение коорди-


x		* x x x dx .	(2.55)

Выражение для среднего значения любого оператора

ˆ F

имеет вид

ˆ				ˆ		dV .	(2.56)
F			r	F r

Волновую функцию x можно разложить по собственным функциям опе-

ратора

ˆ F

(

ˆ
F	n
	n

		n
n		n

Тогда

ˆ			ˆ	Cm		ˆ
F Cn		n	F	Cm	mdV Cn Cm	n F mdV
n				m	n ,m
				m dV		2	(2.57)
Cn Cm	m n			m dV	mCn Cm nm n Cn
n ,m					n ,m	n
Таким образом, среднее значение оператора						ˆ
Таким образом, среднее значение оператора						F определяется суммой соб-
ственных значений этого оператора, взятых с весовыми множителями							Cn	2 ,

определяющими вероятность реализации данного собственного состояния n в волновой функции x .

Для того, чтобы сделать запись квантово-механических выражений более компактной удобно ввести обозначения Дирака, которыми мы будем часто пользоваться в дальнейшем.

Обозначения Дирака:

1) для волновой функции вводятся обозначения:

Ψ( ) = |Ψ >, Ψ ( ) = |Ψ >, Ψ (r) = |n >,

Ψ (r) =< |;

=∫

для матричного элемента оператора -

(r) Ψ

(r)dV = n| |m ;

ортонормируемость записывается, как

∫ Ψn(r)Ψm(r)dV =

n m = δnm;

;

эрмитовость означает, что n| |m = ( m| |n )

полнота системы функций записывается в виде

∑ | >< | = 1.

В этих обозначениях выражения для разложения волновой функции и среднего значения оператора (2.56) значительно упрощаются:

\|Ψ >= ∑	\| >,	̂	̂
		= Ψ\| \|Ψ .

§2.5. Дифференцирование операторов по времени

Запишем условие равенства среднего значения производной оператора по времени производной от среднего значения

Ψ|

|Ψ =

Ψ| ̂|Ψ .

(2.58)

Используя нестационарное уравнение Шредингера, получим

∂

Ψ| |Ψ = Ψ|

|Ψ + ∂t

Ψ| |Ψ + Ψ| |

∂t

Ψ = Ψ|

[ , ]|Ψ .

Таким образом,

̂ ̂

[ , ].

(2.59)

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете Квантовая механика и статистическая физика

#
08.02.2019889.03 Кб171KMSF-Chast1-new.docx
#
08.02.20191.91 Mб69KMSF-Chast1-new.pdf
#
08.02.2019683.63 Кб120KMSF-Chast2-new.docx
#
08.02.20191.63 Mб82KMSF-Chast2-new.pdf
#
08.02.201911.4 Mб40Kvantovaya_Mekhanika_Nerelyativistskaya_Teoria.pdf
#
08.02.201934.1 Кб66Moi_zadachi_po_KMSF.docx
#
08.02.20198.18 Mб46Statisticheskaya_Fizika_Chast_1.pdf