§3.3. Потенциальные барьеры
Одномерный
потенциальный барьер определяется
зависимостью потенциальной энергии от
координаты
.
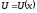Если на каком-то участке координаты x
потенциальная энергия возрастает (или
падает), то говорят об одномерной
потенциальной ступеньке.
Рассмотрим
задачу, когда на одномерную потенциальную
ступеньку налетает частица. Если
выполняется условие, что размер области
изменения потенциальной энергии x
мал по сравнению с волной де Бройля
частицы
,
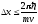то тогда можно считать барьер
прямоугольным, для которого
.
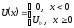В
классическом случае, если энергия
налетающей частицы E
< U0,
то частица с достоверностью отражается
и в правую область не проникает. Если
ее энергия E
>
U0,
тогда частица с достоверностью проходит
над барьером и в правой области она
движется с меньшей скоростью
.
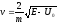В рамках квантово-механического
рассмотрения решается уравнение
Шредингера в области до порога x
< 0 и после порога x
> 0, а затем решения “сшиваются” на
границе (x
= 0).
Прямоугольный потенциальный барьер.
Пусть
на прямоугольный потенциальный барьер
(Рис.3.6) слева падает поток частиц с
полной энергией
,
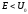меньшей величины барьера.
Рис.3.6. Прохождение частицы сквозь прямоугольный потенциальный барьер.
Потенциальная энергия
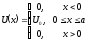(3.25)
Разобьем пространство на три части I, II и III. В I и III областях имеем уравнение Шредингера для свободной частицы:
.
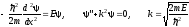(3.26)
Его решения:
I
область
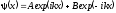, (3.27)
III
область
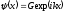. (3.28)
Во II области имеем:
.
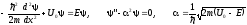(3.29)
Соответствующее решение под барьером
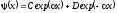(3.30)
Волна exp(ikx) движется в положительном направлении оси x, а волна exp(-ikx) - в обратном. В III области не будет волны в обратном направлении оси x, т.к. из бесконечности нет потока частиц. Окончательно
.
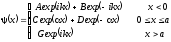(3.31)
На границах полная волновая функция и ее первая производная непрерывны. Эти граничные условия дают систему уравнений для определения коэффициентов A, B, C, D и G.
При
x
= 0
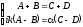. (3.32)
При
x
=
a
.
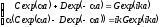(3.33)
Введем коэффициенты отражения и прохождения как отношение плотностей потока
.
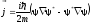(3.34)
В
I
области поток вправо определяется
волной, распространяющейся вдоль оси
x,
.
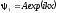Поэтому
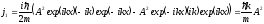(3.35)
Поток
влево в I
области определяется волной
,
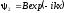а
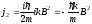(3.36)
Коэффициент отражения определяется
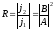(3.37)
Коэффициент
прохождения
(поток пройденной волны определяется
волной
):
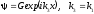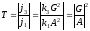(3.38)
В первой паре уравнений (3.32) сложим два уравнения, избавляясь от коэффициента В.
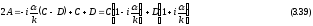
Во второй паре уравнений (3.33) делим на второе уравнение, затем складывая и вычитая, получаем следующие два соотношения:
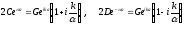
Выражая отсюда 2С и 2D и подставляя их в предыдущее уравнение, имеем
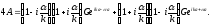
Раскрывая скобки, получаем
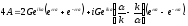
Введем гиперболический косинус и гиперболический синус:
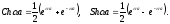
Для
них выполняется теорема Пифагора
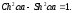
Тогда:
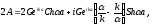
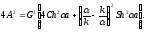
Теперь, раскрывая скобки и учитывая теорему Пифагора, получаем для отношения квадратов:
.
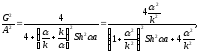
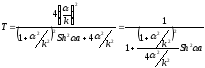(3.40)
Здесь
.
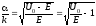Результирующее выражение для коэффициента прохождения имеет вид
.
(3.41)
Исследование коэффициентов прохождения и отражения. То, что коэффициент прохождения не равен нулю при полной энергии частицы меньшей потенциального барьера E < U0 – называется туннельным эффектом. В классической физике ничего подобного нет, туннельный эффект – чисто квантовый эффект.
При условии a >> 1 можно получить для коэффициента прохождения Т:
,
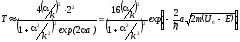или
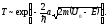
Коэффициент
отражения определяется соотношением
.
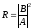Подставляя решения системы уравнений
(3.32) - (3.33), получаем
.
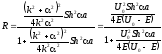(3.42)
Как и должно быть из закона сохранения вероятности
.
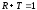(3.43)
Случай E > U0.
Решение
получается тем же путем, как и ранее,
только в области II
имеем решение, описывающее движение
свободной частицы с
.
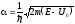В итоге мы получаем те же формулы для
коэффициентов прохождения и отражения,
только ""
меняем на "i"
и "Sh"
на "-iSin":
,
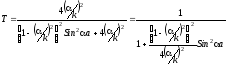(3.44)
.
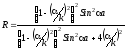(3.45)
В
общем случае мы имеем коэффициент
отражения не равный нулю
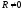(и
),
т.е. частица может отразиться от барьера
и при энергии, превышающей величину
барьера, когда по классической механике
частица проходит с достоверностью над
барьером.
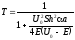
Однако, есть характерные энергии, когда коэффициент отражения равен 0, а коэффициент прохождения равен 1:
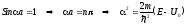
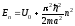(3.46)
При
таких энергиях частица пролетает над
барьером с достоверностью и при квантовом
рассмотрении. Заметим, что при этом
целое число полуволн де Бройля укладывается
на барьере, чему соответствует условие
.
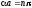Аналогичное решение для коэффициентов прохождения и отражения получаем для барьера в виде прямоугольной ямы, при этом меняется только "U0" на "-U0".
Отметим, что в общем случае коэффициент отражения не равен нулю. Коэффициент прохождения обращается в единицу только для таких энергий когда на размере ямы укладывается целое число полуволн де Бройля.
Барьер произвольной формы.
Если
барьер U
= U(x)
произвольной формы, то задачу о прохождении
частицы можно решить приближенно. Пусть
E
= const
и тогда равенство E
= U(x)
определяет 2 точки a
и b,
где частица классически “входит” и
“выходит” из барьера. Сам барьер можно
представить в виде суммы прямоугольных
барьеров, причем каждый из них рассматривать
отдельно, как ранее.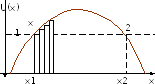 
Рис.3.7. Прохождение частицы сквозь потенциальный барьер произвольной формы.
Приближенно
задачу можно решить, если барьеры
достаточно широкие, и при этом импульс
p(x)
и соответствующая волна де Бройля
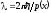медленно меняются на расстоянии ~ .
Это условие называется условием
применения квазиклассического
приближения. В самом деле, воспользуемся
описанием изменения волновой функции
при распространении частицы в пространстве
с постоянным потенциалом, а именно:
,
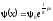где
p(x)
= const
(временной множитель
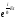не существенен для определения
координатной зависимости). Разбивая
барьер на маленькие прямоугольные
барьеры шириной x,
можно считать, что на ширине x
такого барьера U(x)
= const
и импульс частицы не меняется
.
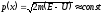Можно записать последовательность
приближенного изменения волновой
функции при переходе от одного барьера
к другому:
………
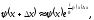
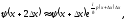
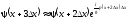Тогда связь волновой функции на выходе из барьера с волновой функцией на входе записывается, как
.
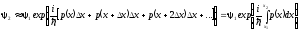Коэффициент прохождения через барьер произвольной формы
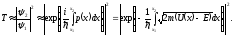
Здесь мы поменяли местами потенциальную и полную энергии частицы. В итоге
.
(3.47)
Выражение (3.47) позволяет найти коэффициент прохождения через барьер произвольной формы в квазиклассическом приближении.