
- •Глава 1. Волновые свойства частиц
- •§1.1. Корпускулярно-волновой дуализм
- •§1.2. Волны де Бройля и их экспериментальное подтверждение
- •§1.3. Статистическое толкование волн де Бройля и соотношение неопределенностей
- •Глава 2. Математический аппарат квантовой механики
- •§ 2.1. Уравнение Шредингера
- •§2.2. Операторы
- •§2.3. Самосопряженные (эрмитовы) операторы и их свойства
- •§2.4. Вычисление средних значений. Обозначения Дирака
- •§2.5. Дифференцирование операторов по времени
- •Глава 3. Уравнение Шредингера в одном измерении
- •§3.1. Одномерная потенциальная яма с бесконечно высокими стенками
- •§3.2. Одномерная потенциальная яма с конечными стенками
- •§3.3. Потенциальные барьеры
- •§3.4. Линейный гармонический осциллятор
- •§3.5. Решение уравнения Шредингера одномерного осциллятора при помощи операторов рождения и уничтожения
- •Глава 4. Момент импульса
- •§4.1. Момент импульса в квантовой механике
- •§4.2. Оператор момента импульса в сферической системе координат
- •§4.3. Оператор квадрата момента импульса в сферической системе координат
- •Глава 5. Физика атомов
- •§5.1. Уравнение Шредингера в центральном поле
- •§5.2. Уравнение для радиальной части волновой функции
- •§5.3. Уравнение для угловой части
- •§5.4. Состояние электронов в атоме. Спин электрона
- •§5.5. Магнитный момент атома
- •Глава 6. Теория возмущений
- •§6.1. Стационарная теория возмущений
- •§6.2. Нестационарная теория возмущений
- •§6.3. “Золотое ” правило Ферми
- •§1.1. Корпускулярно-волновой дуализм 4
§3.2. Одномерная потенциальная яма с конечными стенками
Рассмотрим
одномерную прямоугольную яму со стенками
конечной высоты. 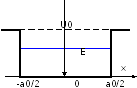
Рис.3.2. Одномерная прямоугольная яма со стенками конечной высоты.
Выберем начало координат на дне ямы симметрично относительно стенок:
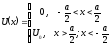 (3.12)
(3.12)
Найдем
сначала решения уравнения Шредингера
внутри и вне ямы. Для получения общего
решения необходимо “сшить” эти решения
на границе ямы. При энергии частицы E
> U0
имеем непрерывный спектр энергий,
частица пролетает над ямой и может иметь
любую энергию. В самом деле, внутри ямы
имеем уравнение
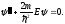 Вводя
Вводя
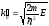 ,
записываем решение в этой области
,
записываем решение в этой области
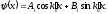 Вне ямы имеем уравнение
Вне ямы имеем уравнение
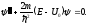 Вводя волновое число
Вводя волновое число
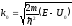 ,
получаем решение вне ямы
,
получаем решение вне ямы
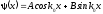 . Сшивая эти решения на границе, получаем,
что любые энергии частицы разрешены.
Таким образом, имеем сплошной спектр
при E
> U0.
. Сшивая эти решения на границе, получаем,
что любые энергии частицы разрешены.
Таким образом, имеем сплошной спектр
при E
> U0.
Рассмотрим подробнее случай, когда энергия частицы E < U0. В этом случае мы получаем дискретный спектр связанных состояний. Для двух областей:
|x|
< a/2
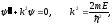 (3.13)
(3.13)
|x|
> a/2
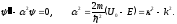 (3.14)
(3.14)
Введем
оператор
четности
с помощью соотношения
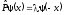 .
Собственные числа оператора четности
могут быть получены, если повторно
подействовать им на исходную волновую
функцию. Тогда получаем, что
.
Собственные числа оператора четности
могут быть получены, если повторно
подействовать им на исходную волновую
функцию. Тогда получаем, что
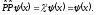 Таким
образом, значения собственных чисел
= 1.
Для значения
= 1, получаем
“четное” состояние, а для
= -1, имеем “нечетное” состояние.
Поскольку
Таким
образом, значения собственных чисел
= 1.
Для значения
= 1, получаем
“четное” состояние, а для
= -1, имеем “нечетное” состояние.
Поскольку
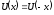 ,
то оператор четности
коммутирует с гамильтонианом
рассматриваемой задачи
,
то оператор четности
коммутирует с гамильтонианом
рассматриваемой задачи
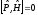 .
(3.15)
.
(3.15)
Из (3.15) следует, что все собственные функции гамильтониана имеют определенную четность. Рассмотрим эти состояния поочередно.
Нечетные состояния. Запишем решения уравнений (3.13) и (3.14) для
нечетных состояний

Рис.3.3. Схематический вид нечетной волновой функции в прямоугольной яме
конечной глубины.
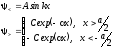 (3.16)
(3.16)
На
Рис.3.3. показано, что частица проникает
вне области ямы, при этом глубина
проникновения частицы под барьер
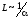 .
.
Из условий непрерывности волновой функции и её производной на границе x = a/2 следует:
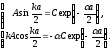 (3.17)
(3.17)
Делением верхнего уравнения на нижнее уравнение получаем, что
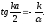 (3.18)
(3.18)
Это
трансцендентное уравнение определяет
энергии разрешенных состояний. То же
самое уравнение получим в силу симметрии
из граничного условия при x
= -a/2.
Введем обозначение
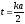 ,
тогда для правой части (3.18) получаем
,
тогда для правой части (3.18) получаем
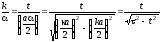 ,
,
где введен параметр мощности ямы:
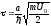 .
(3.19)
.
(3.19)
Для определения спектра надо решить трансцендентное уравнение
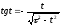 .
(3.20)
.
(3.20)
Рассмотрим
решение этого уравнения графически,
для чего построим отдельно правую и
левую части уравнения. Точки пересечения
дают корни этого уравнения. Из рисунка
видно, что решения имеются не при всех
.
Чем больше мощность ямы ,
тем больше корней уравнения - больше
уровней энергии. При уменьшении
число корней уменьшается. А при мощности
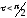 ,
т.е. при
,
т.е. при
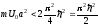 ,
,
корней
соответствующих нечетным состояниям
нет вовсе. Напомним, что t0
= 0 и E0
= 0 не являются корнями, т.к. при этом
решение внутри ямы есть
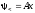 ,
которое не удовлетворяет граничным
условиям.
,
которое не удовлетворяет граничным
условиям.

Рис.3.4. Графическое нахождение собственных энергий нечетных состояний.
Итак, для нечетных состояний, получаем:
-
при мощности ямы
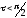 нет дискретных состояний;
нет дискретных состояний;
-
при мощности ямы
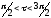 существует 1 нечетное состояние;
существует 1 нечетное состояние;
-
при мощности ямы
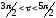 существует 2 нечетных состояний и
т.д.
существует 2 нечетных состояний и
т.д.
Четные состояния. Запишем теперь решения для четных состояний:
 (3.21)
(3.21)
На границе ямы при x = a/2 имеем:
 (3.22)
(3.22)
Откуда получаем новое трансцендентное уравнение
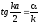 или
или
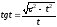 . (3.23)
. (3.23)
В силу симметрии то же уравнение дают граничные условия при x = -a/2. Из графического решения этого уравнения видно, что при всех возможных значениях параметра хоть одно решение есть всегда. Чем больше , тем больше четных решений.
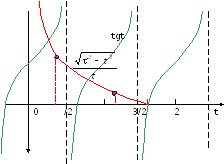
Рис.3.4. Графическое нахождение собственных энергий четных состояний.
Итак,
при мощности ямы
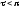 получаем одно четное решение, при
мощности
получаем одно четное решение, при
мощности
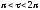 получаем два четных решения и т.д.
получаем два четных решения и т.д.
Рассмотрим теперь “мелкую” яму, для которой << 1. Для такой ямы достаточно легко найти энергию единственного четного состояния (t << 1).
Из
(3.23) следует, что
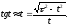 Решая
это уравнение, получаем
Решая
это уравнение, получаем
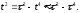 Вспоминая,
что
Вспоминая,
что
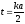 и
и
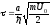 ,
записываем для квадрата волнового
числа
,
записываем для квадрата волнового
числа
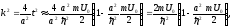
а для энергии
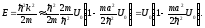 (3.24)
(3.24)
Первый (четный) уровень энергии находится теперь у самого “верха” ямы.
В
одномерной яме с конечными стенками
всегда существует хотя бы одно связанное
состояние. При малой глубине и ширине
(мощности) ямы в яме имеется только один
четный уровень. С ростом U0
и a
растет мощность ямы, и появляются новые
уровни при прохождении параметром
значений
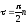 ,
где n
– целое число. Четные и нечетные уровни
появляются по очереди, причем вначале
четные. Качественное поведение волновых
функции низших состояний показано на
Рис.3.5. Возводя в квадрат эти волновые
функции, получаем плотность вероятности
нахождения частицы при данной координате.
,
где n
– целое число. Четные и нечетные уровни
появляются по очереди, причем вначале
четные. Качественное поведение волновых
функции низших состояний показано на
Рис.3.5. Возводя в квадрат эти волновые
функции, получаем плотность вероятности
нахождения частицы при данной координате.
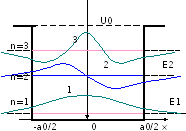
E3
Рис.3.5. Качественное поведение волновых функции низших состояний.
В
одномерной потенциальной яме хотя бы
один уровень существует всегда,
но это не так в трехмерной
потенциальной яме. Для нее существование
хотя бы одного уровня зависит от
“мощности” потенциальной ямы:
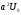 ,
где U0
– глубина ямы, а a
– ее размер. При малых мощностях ямы
энергия частицы тоже должна быть малой,
т.е. частица имеет большую волну де
Бройля, и она как бы не “помещается”
внутри ямы.
,
где U0
– глубина ямы, а a
– ее размер. При малых мощностях ямы
энергия частицы тоже должна быть малой,
т.е. частица имеет большую волну де
Бройля, и она как бы не “помещается”
внутри ямы.
