§2.4. Вычисление средних значений. Обозначения Дирака

Поскольку вероятность найти частицу в элементе объема dV равна 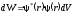, то можно определить средние значения различных физических величин. Напомним, что среднее значение, например координаты, определяется выражением

где вероятность значения dW определяется через плотность вероятности 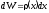. Аналогично получаем для средних значений координаты в состоянии, определяемой волновой функцией _,

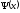Если волновая функция 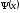уже нормирована, то среднее значение координаты равно

Выражение для среднего значения любого оператора 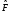_{имеет вид}

Волновую функцию 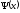можно разложить по собственным функциям оператор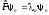а (). Тогда

(2.57)

Таким образом, среднее значение оператора 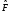определяется суммой собственных значений этого оператора, взятых с весовыми множителями , определяющими вероятность реализации данного собственного состояния n в волновой функции .

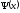Для того, чтобы сделать запись квантово-механических выражений более компактной удобно ввести обозначения Дирака, которыми мы будем часто пользоваться в дальнейшем.

Обозначения Дирака:

1. для волновой функции вводятся обозначения:

;

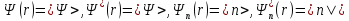2. для матричного элемента оператора - =;

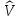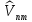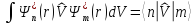3. ортонормируемость записывается, как ;

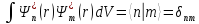4. эрмитовость означает, что ;

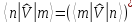5. полнота системы функций записывается в виде .

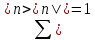В этих обозначениях выражения для разложения волновой функции и среднего значения оператора (2.56) значительно упрощаются:

.

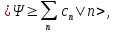
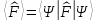§2.5. Дифференцирование операторов по времени

Запишем условие равенства среднего значения производной оператора по времени производной от среднего значения

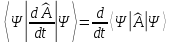. (2.58)

Используя нестационарное уравнение Шредингера, получим

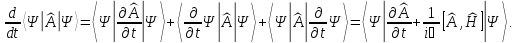
Таким образом,

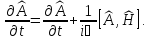(2.59)

Если оператор физической величины не зависит явно от времени, то

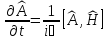(2.60)

Отсюда следует, что среднее значение производной оператора, коммутирующего с гамильтонианом, равно нулю. Такие величины называются сохраняющимися величинами. Очевидно, что сохраняющейся величиной является полная энергия системы, т.к. гамильтониан всегда коммутирует сам с собой. Поэтому, для того, чтобы среднее значение физической величины сохранялось, необходима коммутация квантового оператора этой величины с гамильтонианом.

Глава 3. Уравнение Шредингера в одном измерении

§3.1. Одномерная потенциальная яма с бесконечно высокими стенками

Рассмотрим один из простейших случаев движения частицы вдоль оси x, когда одномерный потенциал

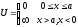
Стационарное уравнение Шредингера

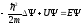(3.1)

для области внутри ямы принимает вид

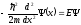. (3.2)

Преобразуем уравнение (3.2) к виду:

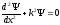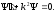, (3.3)

В (3.3) мы ввели волновое число k

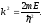(3.4)

Поскольку вне “ямы” потенциальная энергия равна бесконечности, можно ввести “естественные” граничные условия

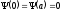. (3.5)

Общее решение уравнения (4.4) удобно представить в виде:

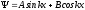. (3.6)

При x = 0 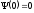, откуда следует, что коэффициент В = 0. При x = а 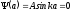, , 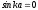, 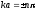n = 1,2,3,... (Для значения n=0 волновая функция тождественно обращается в ноль).

Из (3.4) следует, что

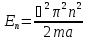_. (3.7)

Мы получили условие квантования уровней энергии в потенциальной яме с бесконечными стенками, поскольку отличные от нуля решения имеются только для целых чисел n. Окончательно решение уравнения (3.3) имеет вид 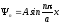. Эти функции являются собственными функциями гамильтониана при данных граничных условиях. Постоянную А находим из нормировки 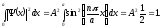Отсюда .

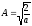Замечание об импульсе. Внутри ямы гамильтониан 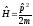и казалось бы, что мы имеем коммутатор оператора импульса с гамильтонианом равным нулю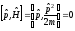 и получаем при этом, что энергия Е и импульс р одновременно измеримы. Однако, это не так. Собственная волновая функция импульса 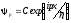не удовлетворяет граничным условиям. Импульс только по модулю имеемет постоянное значение, но сам импульс р не имеет определенного значения.

В окончательном виде собственные функции и энергии:

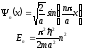(3.8)

Легко построить графики энергии, волновых функций и плотности вероятности для различных значений n. При n = 1 имеем низшее (основное) значение энергии частицы .

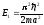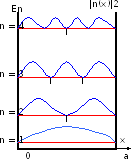
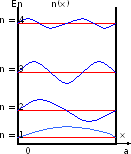
Рис.3.1. Графики энергии, волновых функций и плотности вероятности для различных значений n.

Расстояния между соседними уровнями

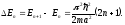(3.9)

Оценим расстояние между уровнями для нескольких случаев:

1) Атомы или молекулы находятся в сосуде с размерами а ~ 1 см. Масса молекулы m ~ 10^-23 г. Энергии квантованы, но расстояние между уровнями энергии

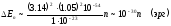
чрезвычайно мало. Для наших приборов они представляют практически сплошной спектр. Дискретность уровней никак не сказывается на движении молекул в таком сосуде;

2) В металле свободные или валентные электроны находятся в “потенциальной яме”, размеры которой пусть также порядка а ~ 1 см. Расстояния между уровнями при массе электронов m ~ 10^-27 г равны

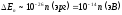
и дискретность уровней по-прежнему не сказывается на движении электронов в металле;

3) Для электронов, находящихся в яме с размерами порядка размеров атома а ~ 10^-8 см, расстояние между уровнями весьма существенно

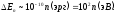
Рассмотрим теперь 3-х мерную прямоугольную яму с бесконечными стенками. Пусть размеры ямы равны: a, b, c. Внутри ямы потенциальная энергия равна нулю: U = 0 при 0  x  a, 0  y  b, 0  z  c. На границах U = . Движение частицы в яме происходит независимо вдоль осей x, y и z. Тогда волновая функция может быть представлена в виде произведения функций

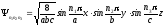(3.10)

При этом энергия равна сумме энергий движений по всем трем осям:

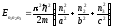при n₁, n₂, n₃ = 1, 2, 3, .... (3.11)

Когда размеры ямы: a, b, c соизмеримы, либо a = b (b = c), либо a = b = c возникают вырожденные уровни энергии, когда одному и тому же значению энергии соответствуют несколько состояний, описываемых различными функциями.