
- •Глава 1. Волновые свойства частиц
- •§1.1. Корпускулярно-волновой дуализм
- •§1.2. Волны де Бройля и их экспериментальное подтверждение
- •§1.3. Статистическое толкование волн де Бройля и соотношение неопределенностей
- •Глава 2. Математический аппарат квантовой механики
- •§ 2.1. Уравнение Шредингера
- •§2.2. Операторы
- •§2.3. Самосопряженные (эрмитовы) операторы и их свойства
- •§2.4. Вычисление средних значений. Обозначения Дирака
- •§2.5. Дифференцирование операторов по времени
- •Глава 3. Уравнение Шредингера в одном измерении
- •§3.1. Одномерная потенциальная яма с бесконечно высокими стенками
- •§3.2. Одномерная потенциальная яма с конечными стенками
- •§3.3. Потенциальные барьеры
- •§3.4. Линейный гармонический осциллятор
- •§3.5. Решение уравнения Шредингера одномерного осциллятора при помощи операторов рождения и уничтожения
- •Глава 4. Момент импульса
- •§4.1. Момент импульса в квантовой механике
- •§4.2. Оператор момента импульса в сферической системе координат
- •§4.3. Оператор квадрата момента импульса в сферической системе координат
- •Глава 5. Физика атомов
- •§5.1. Уравнение Шредингера в центральном поле
- •§5.2. Уравнение для радиальной части волновой функции
- •§5.3. Уравнение для угловой части
- •§5.4. Состояние электронов в атоме. Спин электрона
- •§5.5. Магнитный момент атома
- •Глава 6. Теория возмущений
- •§6.1. Стационарная теория возмущений
- •§6.2. Нестационарная теория возмущений
- •§6.3. “Золотое ” правило Ферми
- •§1.1. Корпускулярно-волновой дуализм 4
§2.3. Самосопряженные (эрмитовы) операторы и их свойства
Непосредственно
измеряемые (“наблюдаемые”) физические
величины вещественны, т.е. все собственные
значения оператора
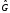 - { gn
} должны быть вещественны. В результате
измерения физической величины, описываемой
оператором
- { gn
} должны быть вещественны. В результате
измерения физической величины, описываемой
оператором
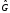 ,
получаем:
,
получаем:
1)
если физическая система (частица)
находится в состоянии, описываемом
собственной функцией
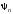 ,
то при измерении получим соответствующее
собственное значение gn
;
,
то при измерении получим соответствующее
собственное значение gn
;
2)
если система (частица) описывается
произвольной функцией
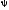 ,
то при измерении наблюдаемой, т.е.
действии оператора
,
то при измерении наблюдаемой, т.е.
действии оператора
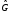 ,
получим линейную комбинацию из собственных
значений gn
- некое среднее значение, которое тоже
вещественно.
,
получим линейную комбинацию из собственных
значений gn
- некое среднее значение, которое тоже
вещественно.
Введем
понятие транспонированного
оператора
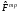 ,
который определяется из соотношения
,
который определяется из соотношения
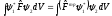 ,
(2.34)
,
(2.34)
т.е.
транспонированный оператор дает тот
же результат, действуя на левую функцию,
что и оператор
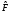 ,
действуя на правую.
,
действуя на правую.
Самосопряженные операторы определяются следующим равенством
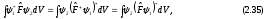
где
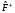 - оператор, сопряженный к оператору
- оператор, сопряженный к оператору
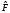 .
.
Если
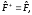 (2.36)
(2.36)
то
этот оператор называется эрмитовым
или самосопряженным
оператором. Можно сказать, что действие
оператора
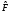 на правую от него функцию совпадает с
действием комплексно сопряженного
оператора на левую функцию:
на правую от него функцию совпадает с
действием комплексно сопряженного
оператора на левую функцию:
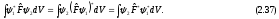
Таким образом, сопряженный оператор – это комплексно сопряженный оператор от транспонированного оператора

Рассмотрим
оператор дифференцирования
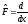 .
Будем считать, что волновые функции
равны нулю на бесконечности. Вычислим
оператор, сопряженный оператору
.
Будем считать, что волновые функции
равны нулю на бесконечности. Вычислим
оператор, сопряженный оператору
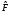 с помощью интегрирования по частям:
с помощью интегрирования по частям:
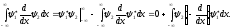
Таким
образом, оператор, сопряженный оператору
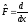 ,
равен
,
равен
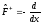
и,
следовательно, оператор
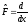 не является
эрмитовым.
Очевидно, что
не является
эрмитовым.
Очевидно, что
оператор
импульса
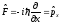 - самосопряженный оператор.
- самосопряженный оператор.
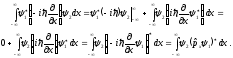
Оператор
координаты
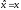 также эрмитов оператор.
также эрмитов оператор.
Рассмотрим
уравнения
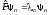 и
и
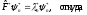
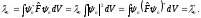 (2.39)
(2.39)
Данное равенство означает, что собственные значения эрмитова оператора вещественны.
Произведение двух эрмитовых коммутирующих операторов есть эрмитов оператор

Пусть
мы имеем дискретный набор собственных
значений и собственных функций эрмитова
оператора
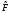 (причем считаем, что нет вырождения,
т.е. все волновые функции
(причем считаем, что нет вырождения,
т.е. все волновые функции
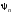 разные для разных собственных значений
разные для разных собственных значений
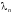 ):
):
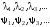
В математике строго доказано, что набор собственных волновых функций эрмитова оператора образует полную систему ортонормированных волновых функций, т.е.
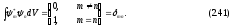
В самом деле, для доказательства ортогональности рассмотрим два равенства

Умножим
слева первое уравнение на
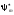 ,
второе на
,
второе на
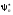 ,
и проинтегрируем. Вычитая второе
уравнение из первого уравнения и
учитывая, что (
,
и проинтегрируем. Вычитая второе
уравнение из первого уравнения и
учитывая, что (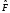 -
эрмитов оператор)
-
эрмитов оператор)
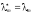 ,
получаем:
,
получаем:
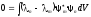 ,
,

Отсюда
следует, что если n
m,
то
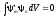 .
Полнота
набора означает, что любую функцию можно
разложить в ряд по функциям
.
Полнота
набора означает, что любую функцию можно
разложить в ряд по функциям
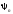 .
.
В
случае, когда имеем вырождение, волновая
функция берется в виде линейной комбинации
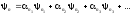 ,
где все волновые функции имеют одно и
то же собственное значение
,
где все волновые функции имеют одно и
то же собственное значение
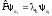 .
При этом линейные комбинации можно
сделать такими, что новые волновые
функции будут ортонормированными.
.
При этом линейные комбинации можно
сделать такими, что новые волновые
функции будут ортонормированными.
Рассмотрим разложение произвольной функции в ряд по системе собственных функций самосопряженного линейного оператора

Коэффициенты
разложения можно получить, умножив обе
части выражения на
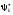 и интегрируя:
и интегрируя:
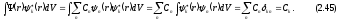
Таким образом,

Квадрат
коэффициента 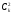
дает вероятность того, что в состоянии,
описываемом
дает вероятность того, что в состоянии,
описываемом
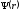 ,
присутствует примесь состояния
,
присутствует примесь состояния
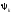 .
.
Если имеем непрерывный спектр значений, тогда волновую функцию раскладываем в интеграл
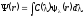 ,
(2.47)
,
(2.47)
где коэффициенты определяются

Волновые функции непрерывного спектра нормируются на - функцию

Свойства - функции.
Функция
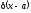 везде равна нулю за исключением точки
x
= a,
где она обращается в бесконечность:
везде равна нулю за исключением точки
x
= a,
где она обращается в бесконечность:
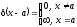 или
или
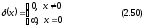
Интеграл
от -
функции равен единице (бесконечность
с мощностью равной 1):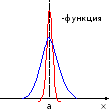
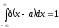 или
или
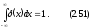
Геометрически -функцию можно рассматривать как предел максимума, стремящегося к бесконечности в точке a и сохраняющего площадь под кривой равной единице. Важное свойство - функции состоит в том, что она “вырезает” из функции в подынтегральном выражении значение этой функции в точке a

Последнее
условие и нормировка позволяет получать
коэффициенты
 .
.
