
Лаба3
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра КЭОП
отчет
по лабораторной работе №3
по дисциплине «Физика конденсированного состояния»
ТЕМА: Исследование температурной зависимости электропроводности полупроводников
Вариант 6
|
СтСтудент гр. 5209 |
|
Хабибулин А.Р, |
|
П Преподаватель |
|
Пухова В. М. |
Санкт-Петербург
2018
Цель работы: изучить механизмы рассеяния заряда на полупроводниках, определяющие температурную зависимость подвижности электронов. Рассчитать зависимость электропроводности полупроводников от температуры.
Описание физических процессов:
Если вывести физическую систему из состояния термодинамического равновесия, то в ней возникнут явления переноса, к которым относятся электропроводность, теплопроводность, термоэлектрические, гальваномагнитные, термомагнитные явления.
Зависимость электропроводности от температуры определяется температурными зависимостями концентрации и подвижности носителей заряда.
Концентрации свободных равновесных носителей заряда в полупроводнике в свою очередь определяются эффективной плотностью энергетических состояний в разрешенных зонах и их фактическим заполнением. На рисунке 1 представлена температурная зависимость концентрации, на которой можно выделить три характерные области: I – ионизации примеси, II – истощения примеси, III – собственной проводимости.

Рис. 1. Температурная зависимость концентрации в полупроводнике
Тангенс угла наклона прямой пропорционален ширине запрещенной зоны
Температурная
зависимость подвижности определяется
временем релаксации. При различных
механизмах рассеяния носителей времена
релаксации также отличаются. К основным
относятся рассеяние на тепловых
колебаниях решетки и на ионизированных
примесях. В теории
 для рассеяния на
колебаниях решетки и
для рассеяния на
колебаниях решетки и
 для рассеяния на
ионизированных примесях. В результате
получаем график, представленный на
рисунке 2.
для рассеяния на
ионизированных примесях. В результате
получаем график, представленный на
рисунке 2.

Рис. 2. Зависимость подвижности от температуры
Температурные зависимости концентрации и подвижности вносят суммарный вклад в определение температурной зависимости электропроводности, график которой представлен на рисунке 3.

Рис. 3. Температурная зависимость электропроводности полупроводника
Исходные данные:
Материал – кремний
Примесь – галлий (акцептор)
Уровень примеси Ea = 0.072 эВ
Обработка результатов
-
Расчет температурной зависимости энергии Ферми при различных концентрациях
Необходимые для расчета данные:
 - постоянная
Больцмана
- постоянная
Больцмана
h = 6.62·10-34 Дж*с– постоянная Планка

m0 = 9.11·10-31 кг – масса свободного электрона
mn* = 0.33·m0 кг – эффективная масса электроная
mp* = 0.81·m0 кг – эффективная масса дырки
 - диэлектрическая
проницаемость кремния
- диэлектрическая
проницаемость кремния
 - диэлектрическая
постоянная
- диэлектрическая
постоянная
Z = 1 – степень ионизации примеси
 - уравнение
электронейтральности для заданного
полупроводника
- уравнение
электронейтральности для заданного
полупроводника
gA = 4 – фактор вырождения акцепторного уровня
 ,
,
 – плотности
состояний, приведенные ко дну зоны
проводимости и потолку валентной зоны
соответственно:
– плотности
состояний, приведенные ко дну зоны
проводимости и потолку валентной зоны
соответственно:
Ec , Ev – положения дна зоны проводимости и потолка валентной зоны
После решения уравнения получаем:
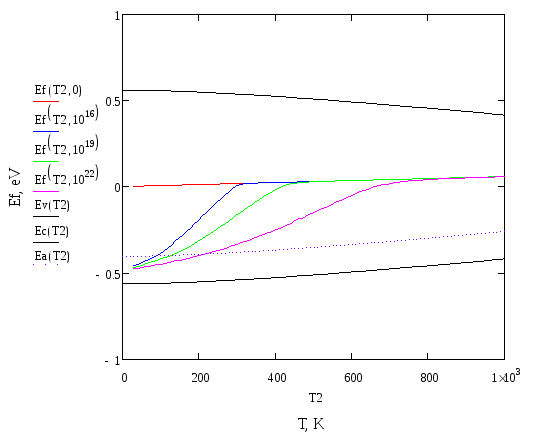
Рис. 4. Температурные зависимости энергии Ферми при различных концентрациях акцепторной примеси
-
Расчет температурных зависимостей концентраций электронов, дырок, ионизированных и неионизированных акцепторов
 - концентрация
электронов
- концентрация
электронов
 - концентрация
дырок
- концентрация
дырок
 - концентрация
ионизированных акцепторов
- концентрация
ионизированных акцепторов
 - концентрация
нейтральных акцепторов
- концентрация
нейтральных акцепторов

Рис. 5. Температурные зависимости концентраций электронов, дырок, ионизированных и нейтральных акцепторов при концентрации 1019 м-3

Рис. 6. Температурные зависимости концентраций электронов, дырок, ионизированных и нейтральных акцепторов при концентрации 1016 м-3


-
Расчет температурной зависимости подвижности электронов и дырок
 - зависимость
подвижности при рассеянии на акустических
колебаниях кристаллической решетки
- зависимость
подвижности при рассеянии на акустических
колебаниях кристаллической решетки
 - для электронов
- для электронов
 - для дырок
- для дырок
Зависимость подвижности при рассеянии на ионах примеси:

NI – концентрация ионизированных примесей
 - зависимость
подвижности при рассеянии на нейтральных
примесях
- зависимость
подвижности при рассеянии на нейтральных
примесях
NN – концентрация нейтральных примесей
 - результирующая
подвижность
- результирующая
подвижность
Построим все кривые для электронов и дырок:

Рис. 9. Температурные зависимости подвижности электронов

Рис.10. Температурные зависимости подвижности дырок
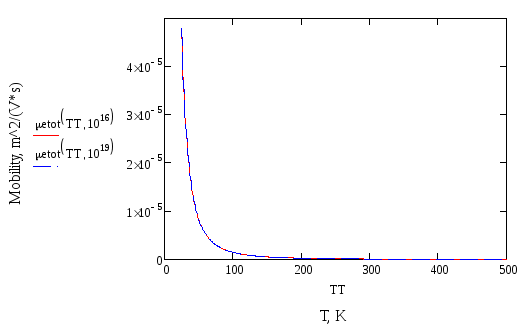
Рис. 11. Степень влияния концентрации примеси на результирующую подвижность электронов

Рис. 12. Степень влияния концентрации примеси на результирующую подвижность дырок
-
Расчет температурной зависимости проводимости полупроводника

Построим соответствующий график:

Рис. 13. Температурная зависимость электропроводности полупроводника
Вывод:
В ходе выполнения данной лабораторной работы были построены температурные зависимости уровня Ферми при различных концентрациях акцепторной примеси. При отсутствии примеси EF слабо зависит от температуры и находится примерно в середине запрещенной зоны полупроводника. При ненулевой концентрации примеси в области низких температур энергия Ферми находится рядом с акцепторным уровнем. По мере роста температуры EF плавно возрастает и, начиная с некоторой температуры (которая зависит от концентрации Na), совпадает с энергией Ферми в отсутствие примеси. Чем больше концентрация примеси, тем наблюдается более пологий рост энергии Ферми.
Также в работе были построены графики зависимости концентрации электронов, дырок, ионизированных и нейтральных примесей от температуры. Чем больше концентрация примеси, тем при большей температуре все примеси оказываются ионизированными. При низких температурах концентрация дырок на много порядков больше концентрации электронов, так как в этом случае основную роль играет примесная проводимость: электроны переходят на акцепторный уровень, при этом в валентной зоне образуются дырки. Далее при более высоких температурах, когда все примеси уже ионизированы, наблюдается собственная проводимость: электроны переходят из валентной зоны в зону проводимости, при этом образуются пары электрон-дырка. Концентрация электронов резко возрастает и стремится сравняться с концентрацией дырок.
Вопрос: Зависимость положения уровня Ферми в полупроводнике с одним типом проводимости.
Ответ: При повышении температуры положение уровня Ферми растет (падает) в полупроводнике p-типа (n-типа) и при высоких температурах достигает середины запрещенной зоны, как в собственном полупроводнике. Это происходит из-за того, что примесь с ростом температуры истощается и в конце концов полупроводник превращается в собственный.

Как видно из формулы, при T=0 уровень Ферми находится между донорным уровнем и потолком зоны проводимости.
Для построения зависимости в области температур, больших нуля, необходимо воспользоваться уравнением электронейтральности:

