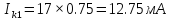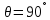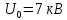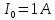MVEL1_Zadachi8_10 (1)
.docx-
Определите амплитуду «самосогласованного» напряжения на сеточном зазоре резонатора с бесконечной собственной добротностью, если амплитуда первой гармоники конвекционного тока на входе в резонатор равна Nstudent*0.75 мА, угол пролета 90О, ускоряющее напряжение Ngroup кВ, ток луча 1А.
|
Дано: |
|
Амплитуда
первой гармоники конвекционного тока
на входе в резонатор
Угол
пролёта
Ускоряющее
напряжение
Ток
луча
|
|
Найти
|
Решение:
В
однозазорном резонаторе электрическое
поле будет сосредоточено в плоском
зазоре, ограниченном параллельными
сетками, а магнитное поле - в объеме
резонатора. С учетом потерь энергии в
стенках резонатора, его обобщенная
эквивалентная схема, представляющая
собой колебательный контур, будет
выглядеть следующим образом: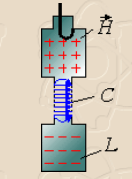
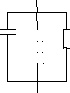
На
данной схеме отражено взаимодействие
электронов с полем зазора (см. вопрос
10) в виде подключённой параллельно
зазору электронной проводимости:
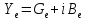 .
Опуская вывод формул из [1] (стр. 74-75),
скажем, что наведённый ток содержит
активную составляющую Iн1,
находящуюся в фазе с напряжением на
зазоре, и реактивную составляющую Iн2,
сдвинутую по фазе относительно напряжения
на 90⁰.
Соответственно, можно определить
активную и реактивную составляющие
проводимости электронного потока:
.
Опуская вывод формул из [1] (стр. 74-75),
скажем, что наведённый ток содержит
активную составляющую Iн1,
находящуюся в фазе с напряжением на
зазоре, и реактивную составляющую Iн2,
сдвинутую по фазе относительно напряжения
на 90⁰.
Соответственно, можно определить
активную и реактивную составляющие
проводимости электронного потока:
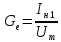 ;
;
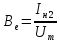 .
Эти проводимости зависят от угла пролёта:
.
Эти проводимости зависят от угла пролёта:
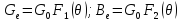 ,
где
,
где
 – проводимость потока по постоянному
току. Графики функций
– проводимость потока по постоянному
току. Графики функций
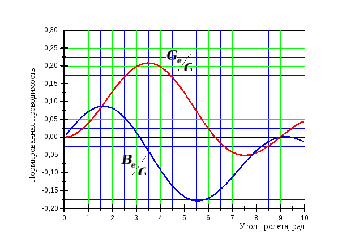
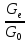 и
и
 показаны на рисунке ниже.
показаны на рисунке ниже.
Отношение
амплитуды наведённого тока к амплитуде
конвекционного тока называют коэффициентом
взаимодействия М потока электронов с
полем зазора:
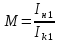
Для
плоского зазора с однородным полем:
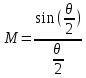
По
графику для угла пролёта
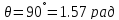 найдём отношение
найдём отношение
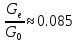 ,
тогда
,
тогда
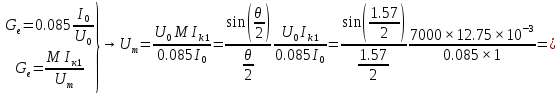
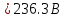
-
Прокомментируйте формулу для мощности взаимодействия электромагнитного поля и потока заряженных частиц. В чем заключается сложность нахождения данного интеграла?
Свяжите решение с задачей №8.
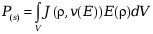
Данная
формула позволяет вычислить мощность
взаимодействия электромагнитного поля
и потока заряженных частиц в пространстве
их взаимодействия. Плотность потока
заряженных частиц
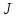 зависит от объёмной плотности заряда
зависит от объёмной плотности заряда
 и скорости частиц
и скорости частиц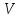 ,
а скорость, в свою очередь, - функция
поля E,
что также зависит от
,
а скорость, в свою очередь, - функция
поля E,
что также зависит от
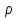 .
Таким образом, сами летящие заряды
создают поле, и это поле действует на
эти же заряды. Специфика данного
взаимодействия разная в разных приборах.
Задачу такого типа называют
«самосогласованной».
.
Таким образом, сами летящие заряды
создают поле, и это поле действует на
эти же заряды. Специфика данного
взаимодействия разная в разных приборах.
Задачу такого типа называют
«самосогласованной».
Сложность «самосогласованной» задачи состоит в её решении – вычислении интеграла – так как трудно учесть такое количество факторов. Так, для нахождения плотности потока нужно знать скорость частиц, которая находится из уравнений движения (например, законов Ньютона или кинетического уравнения Больцмана) и напряженность поля, которая находится из уравнений Максвелла, а также принять во внимание граничные условия, которые определяются параметрами пространства взаимодействия. В частных случаях удаётся найти аналитическое решение с использованием понятия «электронная нагрузка».
В задаче 8 рассматривался энергообмен в зазоре конечной ширины, где в отличие от бесконечно узкого зазора, изменяется и скорость, и взаимное положение электронов. Ускоренные электроны пролетают через зазор за меньшее время, чем замедленные, поэтому коэффициент взаимодействия M для ускоренных электронов оказывается больше, чем для замедленных. В результате ускоренные электроны приобретают большие скорости, чем замедленные, т.е. в целом электронный поток на выходе резонатора имеет большую кинетическую энергию, чем на входе. Избыток кинетической энергии электроны получают от электромагнитного поля зазора, что и отражено на эквивалентной схеме резонатора в виде включённой параллельно зазору электронной проводимости.
Средняя мощность взаимодействия поля зазора с электронным потоком может быть найдена по формуле:
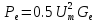 ,
где
,
где
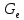 - проводимость электронного потока.
- проводимость электронного потока.
Подставив
значения из задачи 8, получим
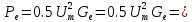
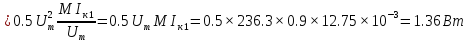
Положительная мощность соответствует передаче энергии от поля электронному потоку.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. А.Д.Григорьев, В.А.Иванов, С.И.Молоковский. Микроволновая электроника. СПб.: Издательство «Лань», 2016. 496 с.
2. В.А.Иванов, Молоковский С.И.. Мультимедийный учебник по курсам «Микроволновые полупроводниковые приборы» и «Электровакуумные приборы СВЧ», 2001, СПбГЭТУ.