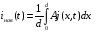me_5_10_1_______7_2
.docx7,2 балл
Малиновский Андрей Васильевич гр. 2205 Ngrup+Nstudent=5+10=15
Задание №1
Рассчитайте энергию кванта микроволнового излучения с частотой 15 ГГц. Какой температуре соответствует эта энергия? Сравните эту энергию с энергией связи молекулы воды. До какой температуры нужно нагреть эту молекулу, чтобы ее ионизовать?
|
Дано:
Решение:
Энергия кванта микроволнового излучения меньше, чем энергия ионизации молекулы воды на несколько порядков. 4.
|
1 балл
Задание №2
Какая плотность мощности микроволнового излучения считается допустимой в быту и на производстве по стандартам РФ? По международным стандартам?
|
По стандартам РФ плотность мощности микроволнового излучения считается допустимой в быту 10мкВт/см2 и на производстве 25мкВт/см2 на расстоянии 50 см. По международным стандартам плотность мощности микроволнового излучения считается допустимой в быту 5-30мкВт/см2 на расстоянии 5 см (МЭК).
|
0,2 балл Где вторая часть задачи?
Задание №3
Информацию о галактическом окружении человечество получает из космоса со спутников, используя микроволновые каналы связи. Выберите один из снимков, полученных с рентгеновского телескопаHubble (http://hubblesite.org/gallery/album/entire), который Вам более всего нравится
|
Понравившийся мне снимок с рентгеновского телескопа Hubble.
|
1 балл
Задание №4
Область взаимодействия составляет L=0.1*15 мм. Рассчитайте угол пролета и коэффициент взаимодействия для этой области для вакуумного прибора с ускоряющим напряжением 10 кВ на частоте 10 ГГц. Как нужно изменить длину L, чтобы этот угол пролета реализовать в полупроводниковом приборе?
|
Дано: L=1.5*10-3м; U=10кВ; f=10ГГц. Для вакуумного прибора:
Угол
пролета
Коэффициента
взаимодействия
Для полупроводникового прибора: При
напряженности поля большей 10 кВ/см
скорость дрейфа носителей достигает
скорости насыщения и обозначают
Длина
области взаимодействия в полупроводниковом
приборе при таком же угле пролета как
и в вакуумном приборе
|
1 балл
Задание №5
Параметры вакуумного прибора: ток 100мА, ускоряющее напряжение 15 кВ. диаметр потока 5 мм.
Полупроводникового: уровень легирования 10*1016см -3 , напряжение 25В, толщина токового канала 1мкм.
Рабочая частота приборов – 5 ГГц. Рабочая температура 400К.
Объёмная плотность заряда
 для
вакуумного прибора характерно ускоряющее
напряжение 15000В, ток 100мА, диаметр
электронного потока 5мм
для
вакуумного прибора характерно ускоряющее
напряжение 15000В, ток 100мА, диаметр
электронного потока 5мм
|
Вакуумный прибор n=5,976*10^14(м^-3)
|
Полупроводниковый прибор
n
|
Для п/п прибора характерная объемная плотность заряда n, на несколько порядков больше, чем в вакуумном.
Максимальная скорость движения заряженных частиц
|
Вакуумный
прибор
|
Max
скорость это скорость насыщения, т.е.
vнас=
|
т.е. max скорость движения заряженных частиц в вакуумном приборе больше чем в полупроводниковом
Длина
области взаимодействия для угла пролета
 -радиан
-радиан
![]() ,тогда
,тогда![]()
|
Вакуумный прибор Взяв максимальную скорость движения заряженной частицы получим:
|
П/П прибор Взяв максимальную скорость движения заряженной частицы
|
Расчет микропервианса, и «плазменной» частоты для вакуумного прибора.


Расчет параметров для полупроводникового прибора: рабочая «ширина» прибора,
обеспечивающая мощность, эквивалентную вакуумному прибору, длина Дебая, плазменная
частота
Расчет плазменной частоты:

Расчет длины Дебая:

1 балл
Задание №6
Можно ли в полупроводниковых приборах обеспечить скоростную модуляцию заряженных частиц, используя начальную часть поле-скоростной характеристики? На каком расстоянии будет обеспечиваться модуляция плотности зарядов? С какой средней скоростью будет двигаться электрон в приборе, с характерным размером области взаимодействия 0.1мкм и приложенным напряжением 10В? Материал – арсенид галлия.
|
(Сплошная линия соответствует арсениду галлия) На начальном участке в области «низких» полей скорость пропорциональна напряженности электрического поля. Значит можно управлять скоростью, изменяя напряженность поля.При напряжении 10 В и области взаимодействия 1 мкм напряженность поля достигнет значения 1МВ/см > 10 кВ/см следовательно скорость будет постоянна и равна 105м/с.
|
0 балл
Задание №7Определите коэффициент шума усилительного прибора в дБ, если его эффективная шумовая температура 110 К. Рассчитайте эффективную шумовую температуру двух таких приборов, включенных каскадно, если коэффициент усиления каждого13 дБ.
|
Дано:
Найти:
Решение:
Коэффициент шума каскадно включенных активных устройств определяется по формуле
Фриза:
Здесь:
Ответ:
|
1 балл
Задание №8
Определите амплитуду «самосогласованного» напряжения на сеточном зазоре резонатора с бесконечной добротностью, если амплитуда первой гармоники конвекционного тока на входе в резонатор равна 10 мА, угол пролета 90О, ускоряющее напряжение 5 кВ, ток луча 1А.
|
Так как резонатор имеет бесконечную добротность то его КПД = 1 , а I0=Iлуча Дано: Im1=6мА, I0=1А, η=1, θ=1,571. Найдем
коэффициент взаимодействия
Выразим напряжение на сеточном резонаторе
|
0 балл
Задание №9
Объясните, где «работает» формула Найквиста, а где Ван-дер-Зила. В чем разница введения понятий «эффективная» шумовая температура и «эффективное» шумовое сопротивление?
|
Формула
Найквиста.
Формула Найквиста для теплового шума в случае термодинамического равновесия. В реальных приборах условия равновесия нарушаются по причине наличия встроенных или приложенных «греющих» электрических полей, которые изменяют энергию электрических зарядов, и следовательно величину шумовых флюктуаций. Формула Ван дер Зила
Эта
формула определяет средний квадрат
шумового тока
Формула Ван дер Зила сложнее формулы Найквиста, но она имеет более широкий диапазон применения, и детальнее отражает физику возникновения шумов. Естественно, что в случае термодинамического равновесия эта формула должна трансформироваться в формулу Найквиста.
Вводя
понятие эффективной шумовой температуры
Выражение
|
1 балл
Задание №10
![]() Прокомментируйте
формулу для мощности взаимодействия
электромагнитного поля и потока
заряженных частиц. В чем заключается
сложность нахождения данного интеграла
Прокомментируйте
формулу для мощности взаимодействия
электромагнитного поля и потока
заряженных частиц. В чем заключается
сложность нахождения данного интеграла
|
Мощность взаимодействия:
Так как первый множитель под интегралом зависит от второго, второй множитель зависит от переменных, от которых зависит и первый множитель, приходится решать самосогласованную задачу.
В среднем за период эта мощность представляется выражением
Для одномерного случая:
Это выражение закона Джоуля-Ленца для переменного во времени тока.
|
1 балл


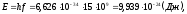





 .
.
 .
Значение этой скорости при температуре
образца 300К практически одинаково для
всех полупроводников и составляет
105м/c.
.
Значение этой скорости при температуре
образца 300К практически одинаково для
всех полупроводников и составляет
105м/c.

 6*10^16
(см^(-3))
6*10^16
(см^(-3)) Max
скорость это скорость света
Max
скорость это скорость света м/с
м/с м/с
м/с




 .
. .
.


 или эффективной шумовой проводимости
или эффективной шумовой проводимости
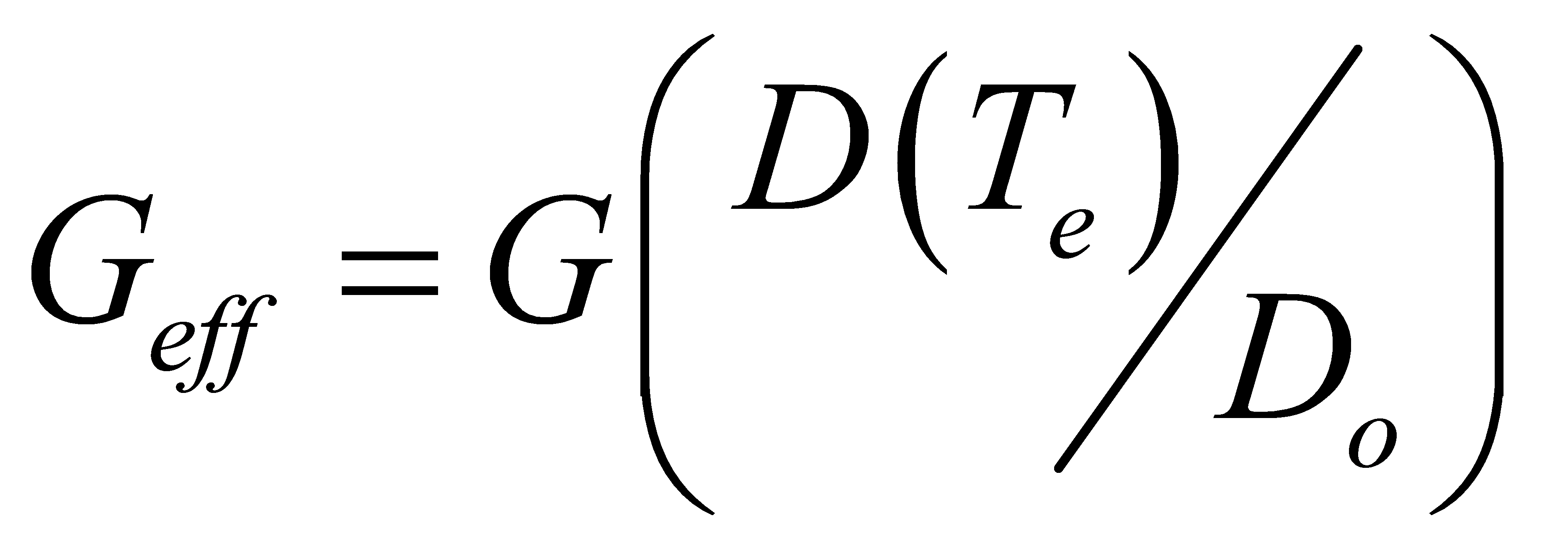 ,
получим обычную запись формулы
Найквиста для отсутствия термодинамического
равновесия:
,
получим обычную запись формулы
Найквиста для отсутствия термодинамического
равновесия: