
me_5_6_1________6_6
.docx
6,6 балл
Земцовская Вера Сергеевна. Группа №2205. Ngrup-5
Nstudent-6
1) Рассчитайте энергию кванта микроволнового излучения с частотой (Ngrup+Nstudent) ГГц. Какой температуре соответствует эта энергия? Сравните эту энергию с энергией связи молекулы воды. До какой температуры нужно нагреть воду, чтобы произошла ионизация?
Дано:
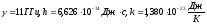
Решение:
-
Определим энергию кванта микроволнового излучения:
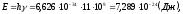
-
Энергия
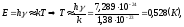
-
Энергия связи молекулы воды:
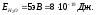
-
Сравним полученную энергию кванта микроволнового излучения с энергией связи молекулы воды:
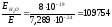 ,т.е.
энергия кванта микроволнового излучения
в 109754 раз меньше энергии связи молекулы
воды.
,т.е.
энергия кванта микроволнового излучения
в 109754 раз меньше энергии связи молекулы
воды.
-
Определим температуру воды, которая соответствует ионизации молекул:
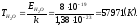
Ответ:
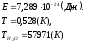
Энергия кванта микроволнового излучения в 109754 раз меньше энергии связи молекулы воды.
1 балл
2.Какая плотность мощности микроволнового излучения считается допустимой в быту и на производстве по стандартам РФ? По международным стандартам? Оцените, как повысится температура тела человека за 8 и 24 часа при максимально допустимом уровне. В расчетах потерями тепла на внешнее охлаждение тела – пренебречь. Опишите особенности нагрева в разных частотных диапазонах.
Дано:
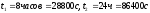
Таблица.1. Плотность мощности допустимого микроволнового излучения:
|
|
В быту |
На производстве |
|
По стандартам РФ |
10 мкВт/см^2 на 50 см |
25 мкВт/см^2 на 50 см |
|
По международным стандартам |
1 мВт/см^2 на 5 см |
1 мВт/см^2 на 5 см |
Решение:
R – допустимая плотность мощности микроволнового излучения.
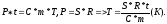
Поскольку человек в среднем на 80% состоит из воды, то примем его теплоёмкость равной 0,8 от теплоёмкости воды.
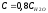
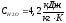
Используемые параметры: масса человека и площадь поверхности тела:
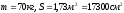
На производстве
по МС за t1 температура
человека повысится на: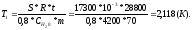
В быту по
МС за t2 температура
человека повысится на:
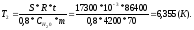
Ответ: T1= 2,118 К , Т2=6,355 К.
0,8 балл
3.Информацию о галактическом окружении человечество получает из космоса со спутников, используя микроволновые каналы связи. Выберите один из снимков, полученных с рентгеновского телескопа Hubble(http://hubblesite.org/gallery/album/entire), который Вам более всего нравится.

1 балл
Object Names: Proxima Centauri, Alpha Centauri C
http://hubblesite.org/newscenter/archive/releases/2013/22/image/b/
4.Область взаимодействия некоторого прибора составляет L=0.1*(Ngrup+Nstudent) мм. Рассчитайте угол пролета и коэффициент взаимодействия для этой области для вакуумного прибора с ускоряющим напряжением (Nstudent) кВ на частоте (Nstudent) ГГц. Как нужно изменить длину L, чтобы этот угол пролета реализовать в полупроводниковом приборе?
Дано:
L=0.1*(5+6) = 1,1 мм, U0 = 6 кВ, γ = 6 ГГц.
Решение:
-
Найдем угол пролёта θпр:
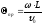 ,
где ω= 2πγ,
а скорость
,
где ω= 2πγ,
а скорость
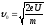 .
.
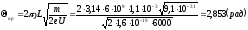
-
Найдем коэффициент взаимодействия М:
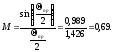
-
Найдем область взаимодействия L1, при которой реализуется данный угол пролёта в полупроводниковом приборе:
Используемая величина:
Скорость
носителей в полупроводниковом приборе
равна
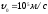
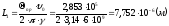
1 балл
-
Сравним области взаимодействия L и L1 в вакуумном и полупроводниковом приборе:
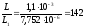 т.е, для полупроводникового прибора
необходимо уменьшить область взаимодействия
в 142 раза.
т.е, для полупроводникового прибора
необходимо уменьшить область взаимодействия
в 142 раза.
Ответ: 1)
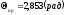
2)
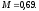
3)
Для реализации угол пролёта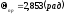 в полупроводниковом приборе необходимо
уменьшить область взаимодействия в 142
раза.
в полупроводниковом приборе необходимо
уменьшить область взаимодействия в 142
раза.
5.Сравните 2 типовых прибора- вакуумный и полупроводниковый по следующим параметрам:
-
Объемная плотность заряда;
-
Максимальная скорость движения заряженных частиц;
-
Длина области взаимодействия для угла пролета
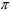 -радиан.
-радиан. -
Для вакуумного прибора рассчитать микропервианс, «плазменную» частоту.
-
Для полупроводникового: рабочую «ширину» прибора, обеспечивающую мощность, эквивалентную вакуумному прибору, длину Дебая, плазменную частоту,
Параметры вакуумного прибора: ток (Nstudent*10)мА, ускоряющее напряжение (Nstudent+ Ngrup) кВ. диаметр потока Ngrup мм.
Полупроводникового: уровень легирования Nstudent*1016см -3 , напряжение 25В, толщина токового канала 1мкм.
Рабочая частота приборов – Ngrup ГГц. Рабочая температура 400К.
Решение:
5.1) Для вакуумного прибора характерные величины: ускоряющее напряжение 11 кВ, ток 60 мА, диаметр электронного потока 5мм. Определим объемную плотность электронов по формуле:
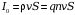 ,тогда
,тогда
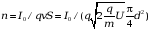
Подставляя числовые значения получим :
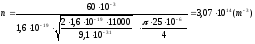
Характерный
уровень легирования (а значит и
максимальное количество носителей
заряда) в полупроводниковых приборах
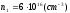 .
.
Сравним объемную плотность зарядов в вакуумном и полупроводниковом приборе:
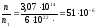 т.е.
в полупроводниковом приборе концентрация
электронов больше, чем на 6 порядков
превышает типовую концентрацию электронов
в вакуумных приборах.
т.е.
в полупроводниковом приборе концентрация
электронов больше, чем на 6 порядков
превышает типовую концентрацию электронов
в вакуумных приборах.
5.2) Для вакуумного прибора:

Для
полупроводникового прибора:
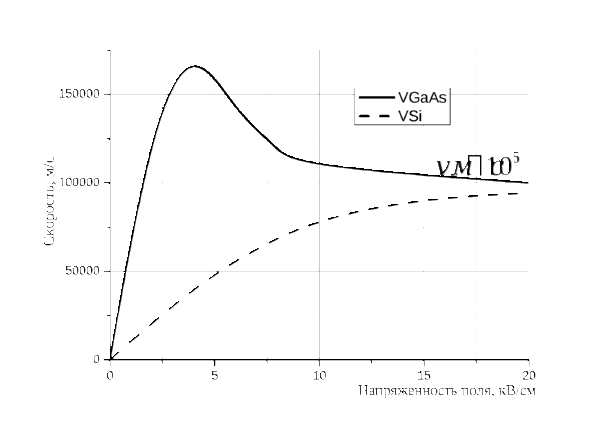
Для
напряженности поля большей 10 кВ/см
скорость дрейфа носителей достигает
некоторого максимального значения,
которое называют скоростью насыщения
и обозначают
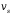 .
Значение этой скорости при температуре
образца 300К практически одинаково для
всех полупроводников и составляет
105м/c.
.
Значение этой скорости при температуре
образца 300К практически одинаково для
всех полупроводников и составляет
105м/c.
В нашем случае U=25 В, h=1 мкм, следовательно Е = 250 кВ/см
Сравним скорости максимального движения заряженных частиц в вакуумном и полупроводниковом приборе:
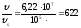 т.е. в вакуумном приборе частицы движутся
в 622 раза быстрее скорости частиц в
полупроводниковом приборе.
т.е. в вакуумном приборе частицы движутся
в 622 раза быстрее скорости частиц в
полупроводниковом приборе.
5.3) Для вакуумного прибора:

Для полупроводникового прибора:
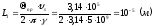
Сравним
длину области взаимодействия для угла
пролета
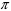 -радиан
в вакуумном и полупроводниковом приборе:
-радиан
в вакуумном и полупроводниковом приборе:
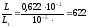 т.е. в вакуумном приборе длина области
взаимодействия в 622 раза больше, чем в
полупроводниковом приборе.
т.е. в вакуумном приборе длина области
взаимодействия в 622 раза больше, чем в
полупроводниковом приборе.
5.4) Микропервианс и «плазменная» частота:
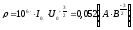
Относительная диэлектрическая проницаемость:ε0=8,85*10-12

5.5) Длина Дебая, плазменная частота:
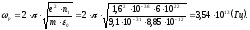

Длина Дебая в диапазоне уровня легирования полупроводникового прибора 6*1022 (м-3) имеет порядок 0.01 мкм, что соизмеримо с характерным размером токового канала.
0,8 балл (ширина).
7)Определите коэффициент шума усилительного прибора в дБ, если его эффективная шумовая температура (100+ Nstudent)К. Рассчитайте эффективную шумовую температуру двух таких приборов, включенных каскадно, если коэффициент усиления каждого 13 дБ.
Дано:
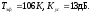 Т0=293
К
Т0=293
К
Решение:
1)Рассчитаем коэффициент шума усилительного прибора:
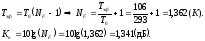
2) Рассчитаем эффективную шумовую температуру двух таких приборов, включенных каскадно.
Определим G (коэффициент усиления в относительных единицах) при Кус=13 дБ:
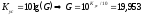
Согласно каскадной формуле:
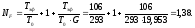
Определим эффективную температуру всего каскада:

Ответ:
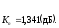
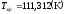
1 балл
8.Определите амплитуду «самосогласованного» напряжения на сеточном зазоре резонатора с бесконечной собственной добротностью, если амплитуда первой гармоники конвекционного тока на входе в резонатор равна Nstudent мА, угол пролета 90О, ускоряющее напряжение Ngrup кВ, ток луча 1А.
Дано:
Бесконечная добротность характеризует резонатор с КПД = 1 ,
Im1=6мА, I0=Iлуча =1А, η=1, θ=1,571,Ua=5 кВ
Решение:
1)Рассчитаем коэффициент взаимодействия:

2) Выразим амплитуду напряжение на сеточном резонаторе:
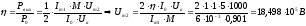
Ответ:
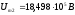
0 балл
9) Объясните, где «работает» формула Найквиста, а где Ван-дер-Зила для расчета шумов. В чем разница введения понятий «эффективная» шумовая температура и «эффективное» шумовое сопротивление?
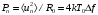 (*)
(*)
Выражение (*) называют формулой Найквиста для теплового шума в случае термодинамического равновесия. В реальных приборах условия такого равновесия нарушаются из-за наличия встроенных или приложенных «греющих» электрических полей, которые изменяют энергию электрических зарядов, а соответственно и величину шумовых флюктуаций. Возникает вопрос: «Как же считать эквивалентные шумовые параметры в таких случаях?». Ответ на этот вопрос можно получить используя формулу А. Ван дер Зила.
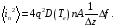
Эта формула
определяет средний квадрат шумового
тока
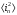 ,
возникающего за счет диффузии
,
возникающего за счет диффузии
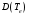 заряженных частиц общим числом
заряженных частиц общим числом
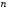 ,
в элементе резистора
,
в элементе резистора
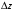 с температурой носителей
с температурой носителей
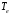 в полосе частот
в полосе частот
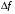 .
В данном выражении
.
В данном выражении
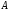 -
поперечное сечение рассматриваемого
элемента.
-
поперечное сечение рассматриваемого
элемента.
Эта формула
сложнее формулы Найквиста, однако, она
имеет более широкий диапазон применения,
да и физику возникновения шумов отражает
детальнее. Естественно, что в случае
термодинамического равновесия эта
формула должна трансформироваться в
формулу Найквиста. Обоснуем введение
таких широко используемых понятий как
эффективная шумовая температура и
эффективное шумовое сопротивление
(проводимость) в случаях, когда нет
термодинамического равновесия. Помножим
правую часть выражения (#) на коэффициент
диффузии
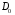 и перегруппируем сомножители:
и перегруппируем сомножители:
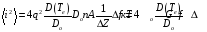 .
.
Вводя
понятие эффективной шумовой температуры
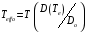 или эффективной шумовой проводимости
или эффективной шумовой проводимости
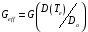 ,
получим обычную запись формулы Найквиста
для отсутствия термодинамического
равновесия:
,
получим обычную запись формулы Найквиста
для отсутствия термодинамического
равновесия:
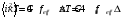
Выражение
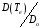 называют шумовым отношением, показывающим
насколько прибор шумит сильнее, чем это
предсказывает формула Найквиста.
называют шумовым отношением, показывающим
насколько прибор шумит сильнее, чем это
предсказывает формула Найквиста.
Следует отметить, что формула Найквиста следует из общих соображений о равновесии линейных двухполюсников и поэтому справедлива для любого реального двухполюсника с той степенью точности, с которой его свойства описываются линейной системой.
Приведенные выражения справедливы в классической области, когда средняя энергия тепловых колебаний намного больше энергии кванта электромагнитного излучения. На более низких частотах справедлива формула Найквиста. Для нелинейных систем и систем с изменяющимися во времени параметрами (в том числе, - флуктуирующими) формула Найквиста, строго говоря, несправедлива. Но в случае слабой нелинейности и малых изменений параметров поправки малы по величине. Для нелинейной чисто резистивной системы в формуле Найквиста вместо активного сопротивления R следует использовать дифференциальное сопротивление в рабочей точке двухполюсника: Rd= dU/dI,
( Гупта, 1978).
Для сравнения шумовых напряжений и токов, действующих в системе, с уровнем равновесных флуктуаций системы удобно выражать шумовое напряжение или ток в виде эквивалентного шумового сопротивления. Величина шумового сопротивления для заданной температуры T определяется по формуле Найквиста (*) и равна сопротивлению R, равновесное шумовое напряжение (ток) которого равен данному шумовому напряжению (току).
Другим используемым представлением является выражение шумового напряжения или тока в виде эквивалентной шумовой температуры. Величина шумовой температуры для заданного сопротивления R определяется по формуле Найквиста (*) и равна температуре T сопротивления R, равновесное шумовое напряжение (ток) которого равен данному шумовому напряжению (току).
Эти представления следует использовать с должной осторожностью, помня о том, что они привязаны к конкретным значениям температуры и сопротивления источника сигнала. В частности, получается, что шумовая температура усилителя зависит от сопротивления источника сигнала, хотя соответствующие напряжения и токи возникают внутри усилителя.
1 балл
Используемая литература:
Материалы для лекции: № 2, №3, №5
Сушков А.Д. Вакуумная электроника: Физико-технические основы.2004. Бонч-Бруевич В.Л., Калашников С,Г. Физика полупроводников. – М.: Наука, 1977.
Букингем М. Шумы в электронных приборах и системах: Пер. с англ. – М.: Мир, 1986. – 399 с.,
http://www.osc.phys.msu.ru/mediawiki/upload/2/26/Ravnshum.pdf
http://www.unn.ru/books/met_files/Yakimov_Noise.pdf
