Rzbor_Poletov
.docx-
Можно ли в полупроводниковых приборах обеспечить скоростную модуляцию заряженных частиц, используя начальную часть поле-скоростной характеристики? На каком расстоянии будет обеспечиваться модуляция плотности зарядов? С какой средней скоростью будет двигаться электрон в приборе, с характерным размером области взаимодействия 0.1мкм и приложенным напряжением 10В? Материал – арсенид галлия.
Типовой ответ.
Задание 6
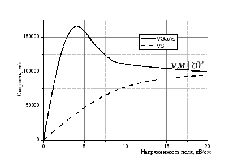
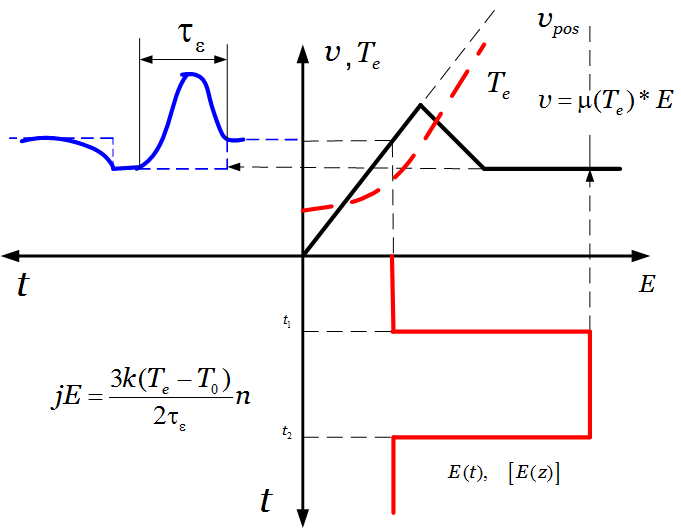
(Сплошная линия соответствует арсениду галлия)
-
На начальном участке в области «низких» полей скорость пропорциональна напряженности электрического поля. Соответственно можно управлять скоростью, изменяя напряженность поля.
-
При напряжении 10 В и области взаимодействия 1 мкм напряженность поля достигнет значения 1МВ/см > 10 кВ/см соответственно скорость будет постоянна и равна 105м/с.
Решение:
Материалы для лекция 3.
Определение
стационарной скорости в случае твердого
тела требует решения двух уравнений, а
также учет характера пространственного
распределения поля
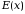 .
.
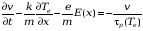
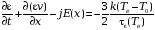 .
.
Эти
уравнения показывают, что в общем случае
между скоростью
 и полем
и полем
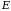 нет локальной связи. Необходимо учитывать
предысторию движения, изменение характера
рассеяния. Процесс установления скорости
может быть в упрощенном варианте описан
следующим образом: заряды под действием
поля Е начинают ускорение и перемещаются
в новую точку, где поле может быть другим.
Кроме того, в среднем через время
нет локальной связи. Необходимо учитывать
предысторию движения, изменение характера
рассеяния. Процесс установления скорости
может быть в упрощенном варианте описан
следующим образом: заряды под действием
поля Е начинают ускорение и перемещаются
в новую точку, где поле может быть другим.
Кроме того, в среднем через время
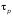 заряды испытают рассеяние импульса,
частично «забывая» о направлении
движения и отдавая часть накопленной
энергии рассеивающему центру. В среднем
этот процесс стабилизируется через
время
заряды испытают рассеяние импульса,
частично «забывая» о направлении
движения и отдавая часть накопленной
энергии рассеивающему центру. В среднем
этот процесс стабилизируется через
время
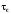 .
Если предположить приложенное поле не
только статическим, но и однородным, а
время его приложения существенно больше,
чем время релаксации энергии
.
Если предположить приложенное поле не
только статическим, но и однородным, а
время его приложения существенно больше,
чем время релаксации энергии
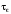 ,
то уравнения () сводятся к более простым:
,
то уравнения () сводятся к более простым:
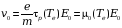
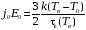
Время релаксации импульса и энергии.
Время
релаксации
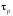 импульса
импульса
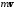 характеризует скорость изменения
(уменьшения) импульса при снятии
возбуждения. Согласно приближению
времени релаксации (1.23)
запишем:
характеризует скорость изменения
(уменьшения) импульса при снятии
возбуждения. Согласно приближению
времени релаксации (1.23)
запишем:
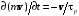
или для одномерного случая:
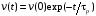 .
.
Величина
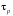 имеет смысл среднего времени свободного
пробега. Если эту величину умножить на
среднеквадратичную тепловую скорость
имеет смысл среднего времени свободного
пробега. Если эту величину умножить на
среднеквадратичную тепловую скорость
 ,
то получим среднюю длину свободного
пробега частицы
,
то получим среднюю длину свободного
пробега частицы
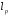 :
:
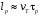 . 101\* MERGEFORMAT (.)
. 101\* MERGEFORMAT (.)
Релаксация энергии частицы происходит с другим характерным временем, т.к. для потери избыточной энергии частице необходимо совершить большое количество актов рассеяния. Это верно для случая упругого рассеяния, которое на практике выполняется ввиду большой разницы в массе взаимодействующих частиц: электронов и ионов (или нейтральных атомов). Перепишем уравнение сохранения энергии (1.24) при снятии внешнего воздействия и без учета пространственной неоднородности потока энергии. В этом случае:
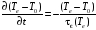 ,
,
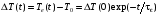 ,
,
где
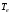 -
текущая электронная температура,
-
текущая электронная температура,
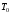 -
равновесная температура, равная
температуре решетки. Тепловые колебания
решетки (фононы) являются разновидностью
не идеальности кристаллической решетки,
на них происходят процессы рассеяния.
-
равновесная температура, равная
температуре решетки. Тепловые колебания
решетки (фононы) являются разновидностью
не идеальности кристаллической решетки,
на них происходят процессы рассеяния.
Следует
заметить, что использование понятия
электронная температура правомерно
лишь в том случае, когда энергетическое
равновесие внутри электронного газа
наступает много быстрей чем энергетическое
равновесие с решеткой. Это может быть
лишь в случае, когда частота межэлектронных
столкновений превышает частоту
столкновений «электрон-решетка», или
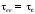 .
Здесь
.
Здесь
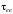 -
характерное время межэлектронных
столкновений.
-
характерное время межэлектронных
столкновений.
По
аналогии с длиной свободного пробега
введем в рассмотрение некое расстояние,
на котором происходит релаксация
энергии. Назовем это расстояние длиной
«остывания» -
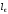 .
В случае подачи электрического поля,
логичнее назвать эту величину длиной
«разогрева». Оценим эту длину следующим
образом:
.
В случае подачи электрического поля,
логичнее назвать эту величину длиной
«разогрева». Оценим эту длину следующим
образом:
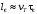 . 202\* MERGEFORMAT (.)
. 202\* MERGEFORMAT (.)
Использование этого понятия важно для анализа особенностей токопереноса в структурах с субмикронными размерами.
Сравним
величины
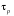 и
и
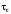 ,
а также
,
а также
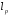 и
и
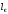 для случая упругих столкновений (типа
электрон-решетка). В этом случае доля
передаваемой энергии при одном акте
столкновения мала, т.е.
для случая упругих столкновений (типа
электрон-решетка). В этом случае доля
передаваемой энергии при одном акте
столкновения мала, т.е.
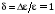 .
Импульс (скорость) изменяется при таком
рассеянии кардинально (прежде всего,
по направлению). Частота актов рассеяния
равна
.
Импульс (скорость) изменяется при таком
рассеянии кардинально (прежде всего,
по направлению). Частота актов рассеяния
равна
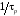 .
Для релаксации энергии требуется большое
количество таких актов рассеяния. При
этом можно записать:
.
Для релаксации энергии требуется большое
количество таких актов рассеяния. При
этом можно записать:
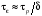 ,
т.е.
,
т.е.
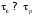 .
Действительно, в реальных полупроводниковых
структурах
.
Действительно, в реальных полупроводниковых
структурах
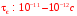 ,
а
,
а
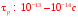 .
Иногда говорят, что «память» на импульс
у электронов намного короче «памяти»
на энергию. Другими словами: процесс
релаксации разогретого электронного
газа в плазме происходит так, что сначала
теряется направленная скорость носителей,
а затем происходит выравнивание
температуры решетки и носителей.
.
Иногда говорят, что «память» на импульс
у электронов намного короче «памяти»
на энергию. Другими словами: процесс
релаксации разогретого электронного
газа в плазме происходит так, что сначала
теряется направленная скорость носителей,
а затем происходит выравнивание
температуры решетки и носителей.
Сказанное
выше, позволяет заключить, что в условиях
упругого рассеяния
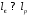 .
При
.
При
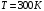 среднеквадратичная скорость составляет
среднеквадратичная скорость составляет
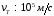 .
Тогда:
.
Тогда:
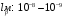 ,
а
,
а
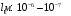 .
Важно отметить, что средняя длина
«разогрева» («остывания») находится в
пределах одного микрона, что соизмеримо
с размерами активных областей современных
микроволновых приборов.
.
Важно отметить, что средняя длина
«разогрева» («остывания») находится в
пределах одного микрона, что соизмеримо
с размерами активных областей современных
микроволновых приборов.
Ответ:
модуляция скорости возможна только на расстоянии длины релаксации импульса – (0.01-0.1) мкм. Далее электрон не «помнит», что было до момента рассеяния. При характерной длине прибора 1мкм и времени воздействия порядка 10-10с получить модуляцию скорости, (а из нее модуляцию плотности) невозможно.
(Дополнительно: релаксация заряда за счет положительной величины максвелловского времени релаксации).
-
Определите амплитуду «самосогласованного» напряжения на сеточном зазоре резонатора с бесконечной добротностью, если амплитуда первой гармоники конвекционного тока на входе в резонатор равна Nstudent мА, угол пролета 90О, ускоряющее напряжение Ngrup кВ, ток луча 1А.
Типовой ответ.
1)КПД резонатора
η=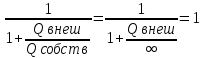
2)Коэффициент взаимодействия
M=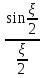 =
=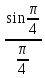 =0.9
=0.9
3)В то же время КПД резонатора:
η=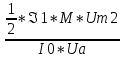
Отсюда
находим амплитуду самосогласованного
напряжения на сеточном зазоре(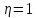 ,
I0=1
A,
Ua=1кВ
, Im1=1
мА)
,
I0=1
A,
Ua=1кВ
, Im1=1
мА)
Um2=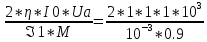 =2,222*106
(В)
=2,222*106
(В)
Решение:
Лекция
6.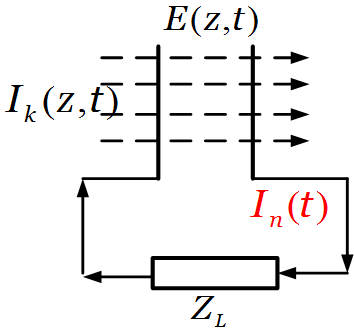
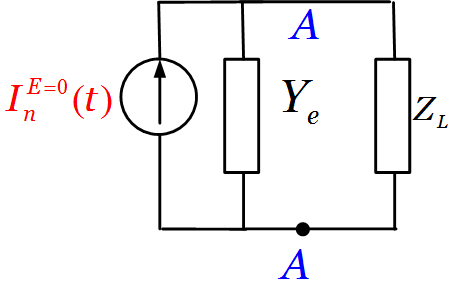
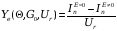
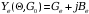
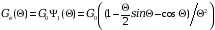
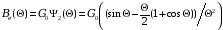
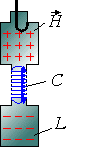
Объемный
резонатор клистрона Эквивалентная
схема и параметры объемного резонатора
клистрона
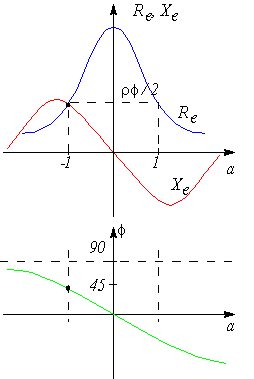
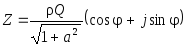

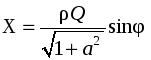
Ответ:
-
Напряжение будет равно нулю, если не подстраивать резонатор.
-
Напряжение равно
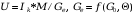 ,
если обеспечить подстройку.
,
если обеспечить подстройку.
-
Сравните 2 типовых прибора- вакуумный и полупроводниковый по следующим параметрам:
-
Объемная плотность заряда;
-
Максимальная скорость движения заряженных частиц;
-
Длина области взаимодействия для угла пролета
 -радиан.
-радиан. -
Для вакуумного прибора рассчитать микропервианс, «плазменную» частоту.
-
Для полупроводникового: рабочую «ширину» прибора, обеспечивающую мощность, эквивалентную вакуумному прибору, длину Дебая, плазменную частоту,
Параметры вакуумного прибора: ток (Nstudent*10)мА, ускоряющее напряжение (Nstudent+ Ngrup) кВ. диаметр потока Ngrup мм.
Полупроводникового: уровень легирования Nstudent*1016см -3 , напряжение 25В, толщина токового канала 1мкм.
Рабочая частота приборов – Ngrup ГГц. Рабочая температура 400К.
Типовой ответ
Объёмная плотность заряда
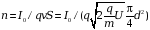 для
вакуумного прибора характерно ускоряющее
напряжение 11кВ, ток 100мА, диаметр
электронного потока 1мм
для
вакуумного прибора характерно ускоряющее
напряжение 11кВ, ток 100мА, диаметр
электронного потока 1мм
Вакуумный прибор
Полупроводниковый прибор
n=1,28*1016(м^-3)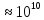 (см^(-3))
(см^(-3))
n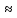 1016
(см^(-3))
1016
(см^(-3))
т.е. объёмная плотность заряда в полупроводниковом приборе на 6-7 порядков больше
Максимальная скорость движения заряженных частиц
Вакуумный прибор
Скорость света с=3*10^8 м/с
Полупроводниковый прибор
Max
скорость это скорость насыщения,т.е.
vнас=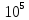 м/с
м/с
т.е. max скорость движения заряженных частиц в вакуумном приборе больше чем в полупроводниковом
Длина
области взаимодействия для угла пролета
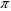 -радиан
-радиан
![]() ,тогда
,тогда![]()
Вакуумный прибор
Полупроводниковый прибор
Взяв
максимальную скорость движения заряженной
частицы получим:![]() =π*3*108/(2*π*109)=0,15(м)=
=150(мм)
=π*3*108/(2*π*109)=0,15(м)=
=150(мм)
![]() =π*105/(2*π*10^9)=5*10-5(м)=
=50мкм
=π*105/(2*π*10^9)=5*10-5(м)=
=50мкм
Ответ на 5.5.
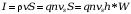 ,
,
Но
необходимо учесть и меньшее напряжение,
т.е. умножить еще на