36. Число Рейнольдса
Число Рейнольдса является основным безразмерным параметром, характеризующим режим течения жидкости: ламинарный или турбулентный.
∙ ∙
=
где n- скорость движения жидкости в трубопроводе, d – диаметр трубопровода, r-плотность жидкости, m – динамическая вязкость жидкости.
37. Ламинарное и турбулентное течения в трубах
Ламинарное течение – это течение, при котором жидкость как бы разделяется на слои, которые скользят относительно друг друга не перемешиваясь. Ламинарное течение стационарно. При этом число Рейнольдса: Re<Reкр=2320
При увеличении скорости или поперечных размеров потока характер течения существенным образом изменяется. Возникает энергичное перемешивание жидкости. Такое течение называется турбулентным. При этом течение нестационарно, так как скорость частиц изменяется беспорядочным образом.
При этом число Рейнольдса: Re>Reкр=2320.
38. Гидравлические сопротивления по длине
Гидравлические сопротивления по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы; Оп ределяются по формуле Дарси-Вейсбаха
2дл =l 2
где L - длина элемента, d - характерный размер сечения, l- коэффициентом потерь на трение по длине.
39. Местные гидравлические сопротивления
Местные гидравлические сопротивления — изменения формы и размера канала,
деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
2
м =x∙ 2
где м- потери на местные сопротивления, x – коэффициент местного сопротивления.
40. Формула Дарси-Вейсбаха
2дл =l 2
где дл- потери на сопротивления по длине, L - длина элемента, d - характерный размер сечения, l- коэффициентом потерь на трение по длине.
l зависит от режима течения жидкости, в частности:
Если Re< 2320, то l= |
64 |
; |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если 2320 <Re< 10 ∙ |
|
, то l= |
0.3164 |
|
; |
|
|
|
|
||||||||||||
|
4 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
∆ |
|
|
|
|
√ |
68 |
|
∆ |
|
||||||
Если 10 ∙ |
<Re< 500 ∙ |
|
, то l=0.11 ∙ ( |
+ |
)0.25 |
||||||||||||||||
|
|
|
|
||||||||||||||||||
|
∆ |
|
∆ |
|
|
||||||||||||||||
Если Re> 500 ∙ |
|
, то l=0.11 ∙ ( |
∆ |
)0.25 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
∆ |
|
|
|
|
|
|
|
|
|
|||||||||
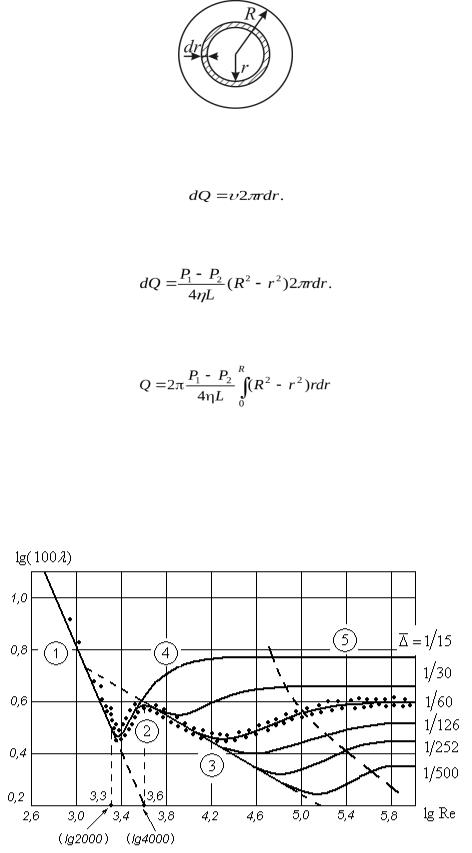
41. Закон Пуазейля
Объем жидкости, протекающей по горизонтальной трубе радиуса R и длиной L ламинарно, можно вычислить следующим образом. Выделим в трубе тонкий цилиндрический слой радиусом r и толщиной dr
Площадь его сечения
. Т.к. слой тонкий, скорость жидкости в нем одинакова 
. За единицу времени слой перенесет объем жидкости:
Подставляя в это выражение 
из формулы, получим:
Интегрируем это выражение по всему сечению трубы:
Окончательно: 
- Формула Пуазейля для ньютоновских жидкостей.
42. График Никурадзе
1-я зона – ламинарный режим: Re<2300;
2-я зона. Далее начинается переходный режим;
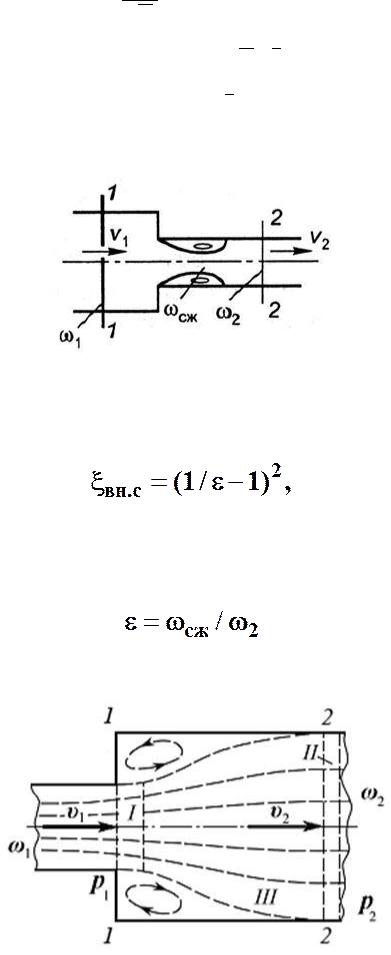
0.3164
3-я зона Гидравлически гладких труб: l= 4 ;
√
4-я зона - зона доквадратичного сопротивления: l=0.11 ∙ (68 + ∆)0.25
5-я зона – зона квадратичного сопротивления: l=0.11 ∙ (∆)0.25
43. Внезапное сужение и внезапное расширение трубопровода.
Рис. Внезапное сужение трубопровода
Коэффициент местного сопротивления при внезапном сужении
где 
— коэффициент сжатия струи, представляющий собой отношение площади сечения сжатой струи в узком трубопроводе 
к площади сечения узкой трубы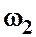 
Рис. Внезапное расширение трубопровода.
При внезапном расширении трубопровода (или русла канала) поток срывается с угла и расширяется не внезапно, как сама труба, а постепенно, причем в кольцевом пространстве между потоком и стенкой образуются вихри, которые и являются причиной потерь энергии, т. е. возникновения сопротивления.
|
( |
− |
)2 |
= |
1 |
2 |
|
|
|
|
|
пот |
2 |
|
|
|
|
|
|
потеря напора при внезапном расширении русла (трубопровода) равна напору, определенному по разности скоростей.
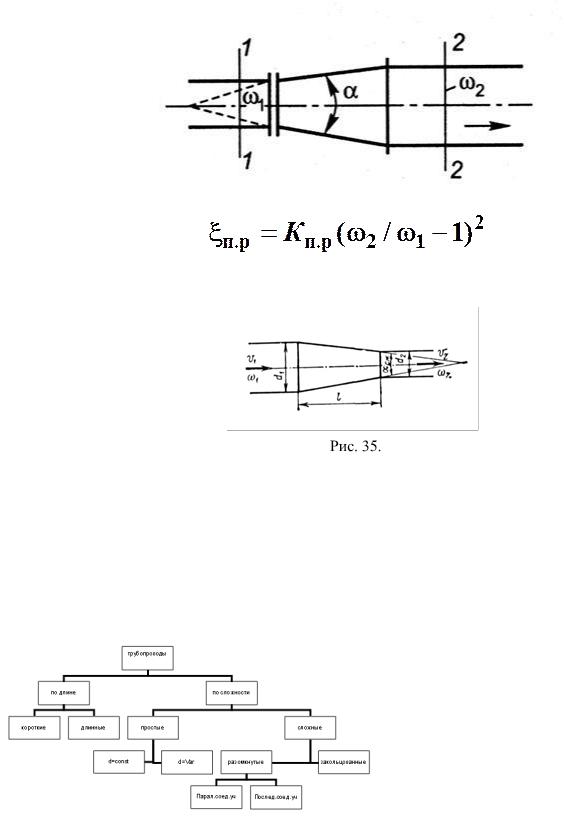
44. Постепенное расширение и постепенное сужение трубопровода
Рис. Постепенное расширение трубопровода.
Коэффициент сопротивления
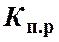— коэффициент смягчения при постепенном расширении, зависящий от угла конусности 
.
Постепенно сужающаяся труба называется конфузором. При течении жидкости в конфузоре скорость вдоль трубы возрастает, а давление уменьшается. Так как жидкость движется от большего давления к меньшему, то в конфузоре отрыв практически отсутствует, и может существовать лишь на выходе из конфузора, в месте соединения конической трубы с цилиндрической. Поэтому сопротивление диффузора всегда больше, чем конфузора с теми же параметрами.
45. Классификация трубопроводов
Простыми трубопроводами называются трубопроводы, не имеющие ответвлений и разветвлений. Сложные трубопроводы имеют последовательно и параллельно соединенные участки.
Короткие трубопроводы - это трубопроводы, местные потери в которых составляют больше 5÷10% от суммарных потерь напора:hм.с.> (5÷10)%Σh