
- •1. Гидростатика. Введение.
- •2. Предмет курса, его цели и задачи.
- •3. Роль гидравлики в нефтегазовом деле.
- •4. Основные понятия и определения.
- •5. Модели жидкостей.
- •6. Основные физические свойства жидкостей (смотри вопрос 4)
- •7. Плотность. Удельный вес (смотри вопрос 4)
- •8. Температурное расширение (смотри вопрос 4)
- •9. Сжимаемость жидкости. Коэффициент объемного сжатия (смотри вопрос 4)
- •10. Вязкость. Кинематическая и динамическая (смотри вопрос 4)
- •11. Неньютоновские жидкости
- •12. Гидростатика. Силы действующие на жидкость
- •13.Гидростатическое давление
- •15. Равновесие жидкости в поле силы тяжести
- •16-17. Основное уравнение гидростатики. Закон Паскаля
- •18. виды давления: избыточное, вакуумметрическое, абсолютное (полное)
- •19. Пьезометрическая высота
- •20. гидростатическое давление на плоскую поверхность
- •21. Понятие центра давления
- •22. Закон Архимеда
- •23. Методы исследования движения жидкости
- •24. Линии и труба тока, элементарная струйка, поток, локальные и средние скорости
- •25. Уравнение расхода жидкости
- •26. Уравнение неразрывности
- •27. Ламинарный и турбулентный режим течения вязкой жидкости
- •28. Опыты рейнольдса
- •29. Уравнение Бернулли для элементарной струйки идеальной и реальной жидкости
- •Уравнение Бернулли для элементарной струйки идеальной жидкости
- •Уравнение Бернулли для элементарной струйки реальной жидкости.
- •30. Геометрический, физический и энергетический смысл уравнения Бернулли
- •31. Гидравлический уклон
- •32. Уравнение для потока жидкости с поперечным сечением конечных размеров
- •34. Виды гидравлических сопротивлений
- •35. Режимы течения жидкости в трубах
- •36. Число Рейнольдса
- •37. Ламинарное и турбулентное течения в трубах
- •38. Гидравлические сопротивления по длине
- •39. Местные гидравлические сопротивления
- •40. Формула Дарси-Вейсбаха
- •41. Закон Пуазейля
- •42. График Никурадзе
- •43. Внезапное сужение и внезапное расширение трубопровода.
- •44. Постепенное расширение и постепенное сужение трубопровода
- •45. Классификация трубопроводов
- •46. Три основные задачи расчета простого трубопровода
- •47. Особенности расчета трубопроводов работающих под вакуумом
- •48. Понятие о расчете сложных трубопроводов
- •49. Трубопровод с насосной подачей
- •50. Истечение жидкости из отверстий в тонкой стенке
- •51. Истечение из сосудов со свободной поверхностью
- •52. Стечение под уровень
- •53. Истечение жидкости через насадки
- •55. Насадки, их виды и области применения.
- •57.Введение в подземную гидромеханику
- •58.Основные понятия теории фильтрации
- •59.Скорость фильтрации. Проницаемость
- •60.Опыты и закон Дарси
- •61.Пределы применимости закона Дарси и причины его нарушения
- •63. Нелинейные законы фильтрации
- •64.индикаторные кривые
- •65. коэф продуктивности скважины
- •66.Установившаяся фильтрация несжимаемой жидкости
- •67.Плоские установившиеся потоки
- •68.прямолинейно-параллельная фильтрация
- •69.дебит и распределение давления при линейной фильтрации
- •70.плоско-радиальная фильтрация жидкости
- •71.понятие о гидродинамическом несовершенстве скважины
- •72.дополнительные фильтрационные сопротивления
- •73.способы расчетов течений в несовершенных скважинах

70.плоско-радиальная фильтрация жидкости
5.2.2. Плоскорадиальное напорное движение несжимаемой
Жидкости. Приток к совершенной скважине. Формула Дюпюи
При плоскорадиальном движении векторы скорости фильтрации направлены по радиусам к оси скважины, поэтому давление и скорость фильтрации зависят только от одной координаты r. При этом во всех горизонтальных плоскостях поле скоростей и давлений будет одинаковым.
Примером плоскорадиального фильтрационного потока является приток к гидродинамически совершенной скважине, вскрывшей горизонтальный пласт бесконечной протяженности на всю толщину h и сообщающейся с пластом через полностью открытую боковую поверхность цилиндра,
отделяющую ствол скважины от продуктивного пласта.
Поток будет также плоскорадиальным при притоке к совершенной скважине радиуса гс (или оттоке от скважины), расположенной в центре ограниченного горизонтального цилиндрического пласта толщиной h и радиусом RK (рис.5.
2).
Если на внешней границе пласта, совпадающей с контуром питания, поддерживается постоянное давление рк, а на забое скважины постоянное давление рс, пласт однороден по пористости и проницаемости, фильтрация происходит по закону Дарси, то объемный дебит скважины определится по формуле Дюпюи:
(5.16)
где μ - динамический коэффициент вязкости.
Закон распределения давления определяется по одной из формул:
(5.17)
либо
(5.18)
либо
(5.19)
Линия р = р(r) называется депрессионной кривой давления. Характерно, что при приближении к скважине градиенты давления и скорости фильтрации рис.5.2 резко возрастают. При построении карты изобар следует учитывать, что радиусы изобар изменяются в геометрической прогрессии, в то время как давление на изобарах изменяется в арифметической прогрессии.
Индикаторная линия - зависимость дебита скважины от депрессии Δp=pK –pC при притоке к скважине в условиях справедливости закона Дарси представляет собой прямую линию, определяемую уравнением Q=KΔp.
Коэффициент продуктивности
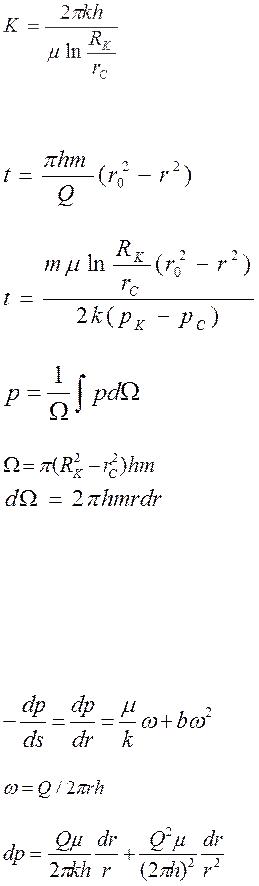
(5.20)
численно равен дебиту при депрессии, равной единице.
Закон движения частиц вдоль линии тока, если при t=0 частица находилась в точке с координатой r=r0, описывается уравнением
(5.21)
или
(5.21,а)
Средневзвешенное по объему порового пространства Q пластовое давление
(5.22)
где
Подставляя выражение для р (5.17), выполняя интегрирование и пренебрегая всеми членами, содержащими rc2:, получим
 (5.23)
(5.23)
Закон распределения давления и формула дебита при нарушении закона Дарси при притоке к совершенной скважине получаются из двучленной формулы
(5.24)
Подставляя выражение для скорости фильтрации
в (5.24) и разделяя переменные, получим
(5.25)
Интегрируя по р в пределах от рс. до рк и по r в пределах от rc,. до Rkбудем иметь
 (5.26)
(5.26)
Решая полученное квадратное уравнение, находим дебит скважины Q. Интегрируя (5.25) по р в пределах от рс. до рк и по r в пределах от rс до RK, найдем закон распределения давления
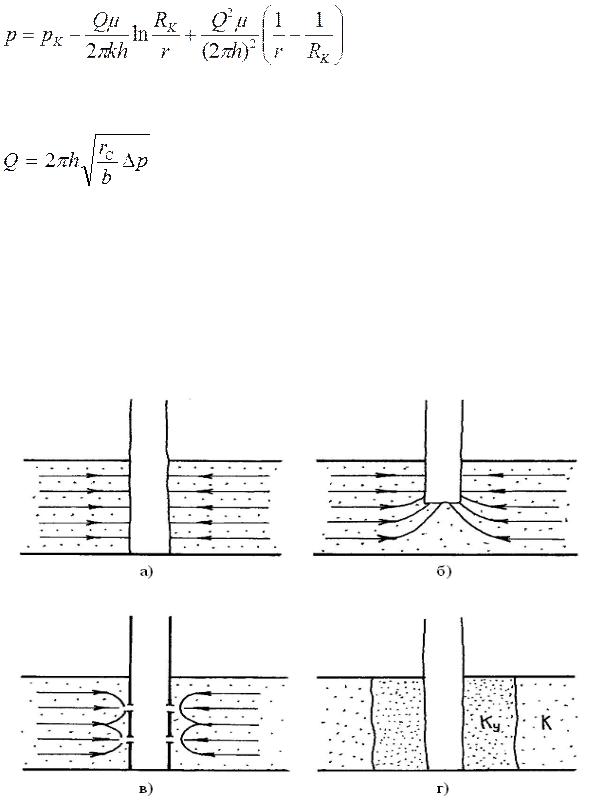
(5.27)
Как видно из (5.26), индикаторная линия при нарушении закона Дарси является параболой.
Если фильтрация происходит по закону Краснопольского, то дебит определяется по формуле
(5.28)
71.понятие о гидродинамическом несовершенстве скважины
Целесообразно выделить следующие три вида гидродинамического несовершенства скважин (рис.4.1):
1по степени вскрытия пласта, когда скважина вскрывает продуктивный пласт не на всю толщину;
2по характеру вскрытия пласта, когда связь пласта со скважиной осуществляется не через открытую боковую поверхность скважины, а только через перфорационные отверстия в обсадной колонне;
3по качеству вскрытия пласта, когда проницаемость пористой среды в призабойной зоне снижена по отношению к естественной проницаемости пласта.
Рис. 4.1. Схематичное изображение гидродинамически совершенной и гидродинамически несовершенных скважин:
а) совершенная скважина; б) несовершенная скважина по степени вскрытия пласта;
в) несовершенная скважина по характеру вскрытия пласта; г) несовершенная скважина по качеству вскрытия пласта
(kу – проницаемость призабойной зоны пласта, k – проницаемость удаленной зоны пласта)
Формула притока в реальную скважину (фактический приток), пробуренную на нефтяной пласт и имеющую все перечисленные виды гидродинамического несовершенства, может быть записана в следующем виде:

, |
(4.3) |
где с1 - безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из-за несовершенства скважины по степени вскрытия продуктивного пласта; с2 - безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из -за
несовершенства скважины по характеру вскрытия продуктивного пласта (перфорация);
sб - безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из -за несовершенства скважины по качеству вскрытия продуктивного пласта бурением (скин -эффект из-за ухудшения проницаемости породы при первичном вскрытии пласта бурением);
sц - безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из -за несовершенства скважины по качеству цементирования (скин -эффект из-за ухудшения проницаемости породы при цементировании обсадной колонны);
sп - безразмерный коэффициент, учитывающий дополнительные фильтрационные сопротивления из -за несовершенства скважины по качеству вскрытия продуктивного пласта перфорацией (скин -эффект изза ухудшения проницаемости породы при перфорации скважины).
Основные и дополнительные фильтрационные сопротивления в зоне дренирования соответственно равны
72.дополнительные фильтрационные сопротивления
См вопрос 71
73.способы расчетов течений в несовершенных скважинах
Процесс течения продукции в пористой среде сопровождается определенными фильтрационными сопротивлениями, которые являются неизвестными. В призабойной зоне скважины возникают дополнительные фильтрационные сопротивления, связанные, во-первых, с наличием самой скважины и, во-вторых, с конкретным ее исполнением.
Для сравнения скважин между собой и оценки каждой конкретной скважины вводятся понятия гидродинамически совершенной скважины и гидродинамически несовершенных скважин.
На рис. 47 приведены схемы гидродинамически совершенной и гидродинамически несовершенных скважин.
Под гидродинамически совершенной будем понимать такую скважину, которая вскрыла продуктивный горизонт на всю его толщину h и в которой отсутствуют любые элементы крепи (обсадная колонна, цементный камень, забойные устройства), т.е. скважина с открытым забоем. При течении продукции в такую скважину фильтрационные сопротивления обусловлены только характеристикой продуктивного горизонта и являются минимально возможными (рис. 47 а).
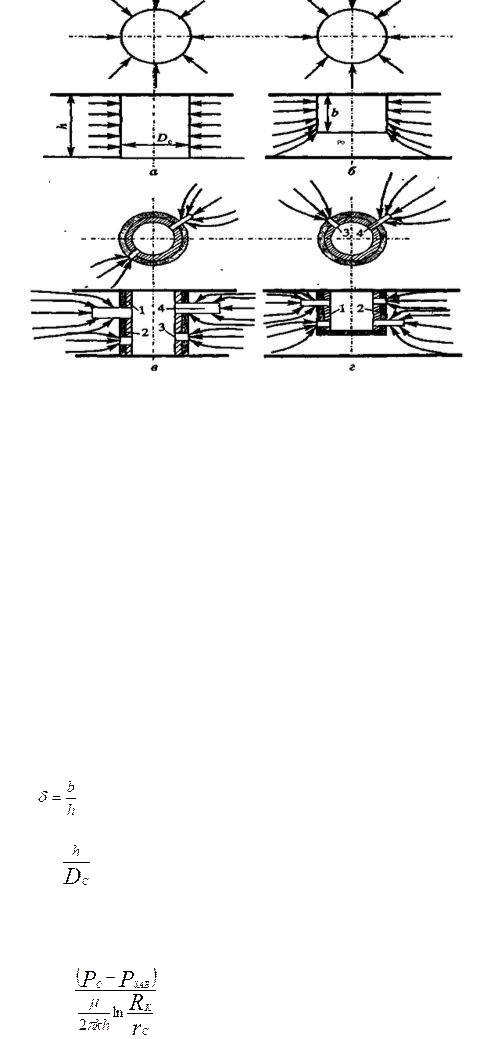
Рис.47. Схемы гидродинамически совершенной (а) и гидродинамически несовершенных скважин: б – по степени вкрытия; в – по характеру вкрытия; г – по степени и характеру вкрытия;
1 – обсадная колонна; 2 – цементный камень; 3 – перфорационное отверстие; 4 – перфорационный канал.
Большинство реальных скважин относятся к гидродинамически несовершенным. Среди гидродинамически несовершенных скважин выделяют:
1.Несовершенные по степени вскрытия - НСВ (рис. 47 б); 2.Несовершенные по характеру вскрытия - НХВ (рис. 47 в);
3.Несовершенные по степени и характеру вскрытия – НСХВ (рис. 47 г).
Для таких скважин и призабойной зоне возникают дополнительные фильтрационные сопротивления, определяемые видом несовершенства.
1.Для скважин несовершенных по степени вскрытия.
Несовершенныеми по степени вскрытия называются скважины, которые вскрывают продуктивный горизонт не на всю толщину.
Введем следующие обозначения:
h – тольщина продуктивного горизонта, м; Dc – диаметр скважины по долоту, м;
b – часть тольщины продуктивного горизонта, вскрытого скважиной, м; d - относительное вскрытие:
, |
(6) |
а – безразмерная толщина пласта: |
|
a = |
(7) |
Как видно из рис. 8.5 б, дополнительные фильтрационные сопротивления для таких скважин связаны с искривлением линий тока (т.е. геометрия течения) и могут быть учтены введением их в уравнение Дюпюи.
Имеем для совершенной скважины:
Qc = |
(8) |

Где rc – радиус скважины по долоту rc=Dc/2/
Знаменатель выражения (8) и есть фильтрационные сопротивления Rф при течении продукции к совершенной скважине, т.е.
 Rф=
Rф=
(9)
С учетом этого выражения (8) запишем в виде:
(10)
Обозначим дополнительные фильтрационные сопротивления через Rдоп. По аналогии с (9) запишем:
(11)
Где С1 – некоторый коэффициент, учитывающий возрастание фильтрационных сопротивлений за счет изменения геометрии течения продукции к несовершенной по степени вскрытия скважине.
Дебит несовершенной по степени вскрытия скважины обозначим через Qнев.
или
(12)
Выражение (12) может быть использовано для расчета дебита несовершенных по степени вскрытия скважин. При этом дополнительные фильтрационные сопротивления учитываются коэффициентом С1
С1 = ƒ (δ, а), (13)
определяемым по специальным графикам (например, по графикам В.И. Щурова).
2.Для скважин, несовершенных по характеру вскрытия
Несовершенными по характеру вскрытия называются скважины, которые вскрывают пласт на всю толщину, но скважина обсажена и проперфорирована.
Ведем следующие обозначения:
n – плотность перфорации н6а один погонный метр, отв/м; l′ - средняя длина перфорационного канала, м;
d′ - диаметр перфорационного канала, м;
- параметр nDc; |
|
- безразмерная длина перфорационного канала |
|
l = l′/Dс |
(14) |
- безразмерный диаметр перфорационного канала |
|
d = d′/Dс |
(15) |
Дополнительные фильтрационные сопротивления для таких скважин связаны с изменением геометрии течения продукции вследствие наличия перфорационных отверстий и каналов. По аналогии с выражением (11) запишем:

|
доп = |
2, |
(16) |
Где С2 – некоторый коэффициент, учитывающий возрастание фильтрационных сопротивлений вследствие изменения геометрии течения продукции из-за наличия перфорационных отверстий и каналов.
Дебит несовершенной по характеру вскрытия скважины обозначим через Qнхб. Тогда по аналогии с (12) запишем:
Qнхб = |
(17) |
При этом коэффициент дополнительных фильтрационных сопротивлений за счет несовершенства |
|
по харктеру вскрытия С2 |
|
C2=ƒ(nDс,l,d |
(18) |
3. Для скважин, несовершенных по степени и характеру вскрытия
В этом случае на фильтрационную картину течения продукции к несовершенной по степени вскрытия скважине накладывается фильтрационная картина течения продукции к перфорированным отверстиям и перфорационным каналам. На рис. 48 показана такая картина течения продукции к несовершенной по степени и характеру вскрытия скважине. Видно, что в I области течение плоско-радиальное и справедливым остается уравнение Дюпюи в виде (4); во II области фильтрационная картина существенно отличается от таковой в I области, что вызвано несовершенством скважины как по степени, так и по характеру вскрытия и появлением дополнительных фильтрационных сопротивлений, учитываемых коэффициентами Cj и С2. Суть вопроса заключается в том, каким образом для такого вида несовершенства взаимосвязаны коэффициенты С, и С2. Для ответа на этот вопрос реальную фильтрационную картину, представленную на рис. 48, заменим схематизированной, которая представлена на рис. 49. Схематизацию течения продукции выполним, введя фиктивную скважину, несовершенную по степени вскрытия, радиус которой rфс. В этом случае рассматривается течение продукции:
- в пределах от Rк до r - как течение к скважине, несовершенной по степени вскрытия (дополнительные фильтрационные сопротивления учитываются коэффициентом С1);
- в пределах от rфс до с - как течение к скважине, несовершенной по характеру вскрытия (дополнительные фильтрационные сопротивления учитываются коэффициентом С2).
Рис. 48. Фильтрационная картина течения продукции к несовершенной по степени и характеру вскрытия скважине:
I – область, в которой фильтрация подчиняется закону Дарси – плоскорадиальная фильтрация; II – область нарушения закона Дарси, в которой возникают дополнительные фильтрационные сопротивления, учитываемые коэффициентами С1 и С2; 1 – обсадная колонна; 2 – цементный камень; 3 – перфорационное
отверстие; 4 – перфорационный канал
Рисунок 49Схематизированная фильтрационная картина течения продукции к несовершенной по степени и характеру вскрытия скважине:
I- область дополнительных фильтрационных сопротивлений к несовершенной по степени вскрытия фиктивной скважине, учитываемых коэффициентом С1;

II - область дополнительных фильтрационных сопротивлений к несовершенной по характеру вскрытия скважине, учитываемых коэффициентом С2; rс. rфс
Для приведенной схемы фильтрационные сопротивления в I области (отRк до rфс) складываются из:
-фильтрационного сопротивления Rф, которое по аналогии с (9) таково:
RФ = |
(19) |
- дополнительного фильтрационного сопротивления, которое по аналогии с (11) таково:
Кксоответственно радиус реальной скважины, радиус фиктивной скважины и радиус контура питания; b - вскрытая часть пласта толщиной h
(20)
Для II области (от. rфс до rс ) фильтрационные сопротивления складываются из: - фильтрационного сопротивления R′Ф, которое по аналогии с (9) таково:
(21)
Где в соответствии с (6) b = h∙δ
Тогда с учетом этого выражения (21) запишем в виде:
R′Ф = |
(22) |
- дополнительного фильтрационного сопротивления, которое по аналогии с (16) таково:
(23)
Дебит несовершенной по степени и характеру вскрытия скважины Qнсхв дя схематизированной картины течения (рис. 8,7) с учетом выражения (19), (120), (21) и (23) таков:
Qнсхв = |
(24) |
Для реальной фильтрационной картины запишем: |
|
Qнсхв= |
, |
(25) |
Где |
- фильтрационные сопротивления при движении продукции от Rк до rc; |
|
 - дополнительные фильтрационные сопротивления за счет несовершенства скважины по степени и характеру вскрытия, определяемые коэффициенты С.
- дополнительные фильтрационные сопротивления за счет несовершенства скважины по степени и характеру вскрытия, определяемые коэффициенты С.
Приравнивая правые части выражений (25) и (24), получим:
,
откуда находим коэффициент С
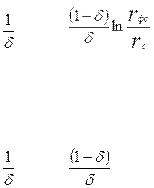
С=С1+ С2+2,3 |
(26) |
Таким образом, коэффициент дополнительных фильтрационных сопротивлений при течении продукции к несовершенной по степени и характеру вскрытия скважине не является простой суммой коэффициентов С1 и С2, а зависит не только от этих коэффициентов, но и относительного вскрытия пласта и радиусов фиктивной (rфс ) и реальной (rc) скважин. Принимая, например, rфс = 10rc, получим:
С=С1+ С2+2,3 |
(27) |
Резюмируя, отметим, что рассмотренные виды несовершенства скважин учитывают только изменение геометрии течения продукции в сравнении с такой для совершенной скважины.
