4. Выбор периода дискретности системы

Период дискретности выберем из условия фильтрации сигналов элементами системы.

В системе имеется три фильтра первого порядка типа с постоянными времени:

Тэл=0,015сек – электрическая постоянная времени двигателя,

Tм=0,96сек – механическая постоянная времени,

Тд=0,5сек – постоянная времени датчика.

Tм и Тд имеет значение одного порядка и ими будет определятся спектр сигналов, действующих в системе.

Выбираем t=1/10, Tм=0,02сек.

сек.

Такая величина периода дискретности позволяет отразить все спектральные составляющие возмущения по усилию натяжения волокна.

Дискретизация звена в передаточной функции электрического двигателя при t=Tд внесет большие искажения в сигналы, действующие в системе. Меньшее значение ошибки будет иметь место если примем Tэ=0, т.е. передаточную функцию электрического двигателя примем в виде:

.

5. Получение передаточной функции системы

Передаточные функции элементов системы управления имеют вид:

Электродвигателя с учетом датчика и алгоритма расчета скорости:

.

Широтно-импульсного модулятора:

W(p)=1,1.

Объекта управления:

Значит, передаточная функция неизменяемой части системы равна:

В данной системе управления корректирующего устройства реализуется на микропроцессорной системе с цифроаналоговым преобразователем на выходе, значит САУ относится к классу дискретных систем с фиксатором нулевого порядка. Для описания дискретной системы используем Z и w преобразования. Для этого выполним ряд преобразований [51].

Передаточная функция неизменяемой части системы:

.

По таблице преобразований от оператора р к оператору z [56]:

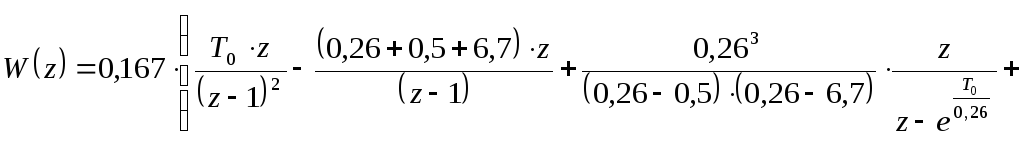
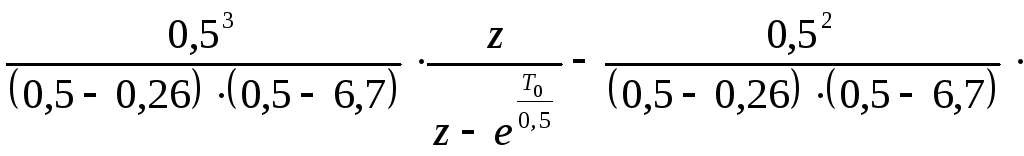
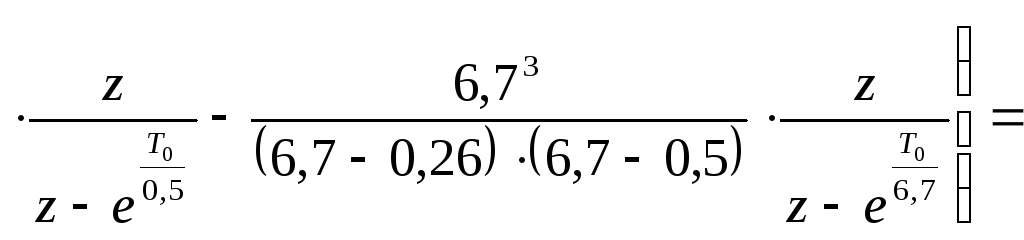
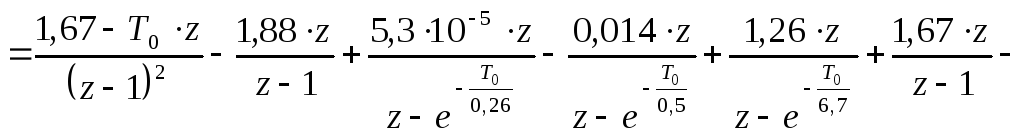
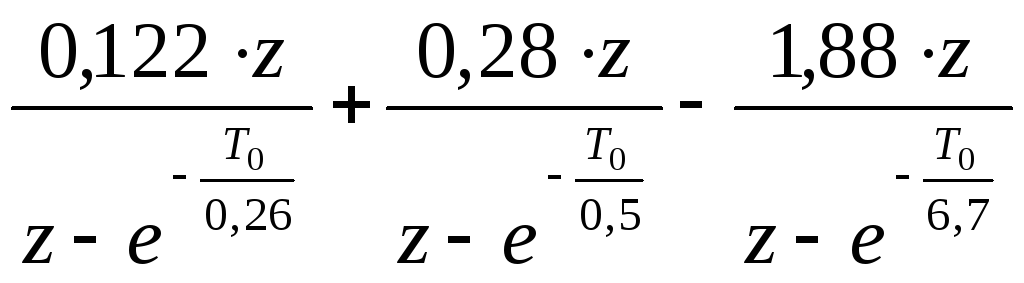
где Т₀ – период дискретизации.

Подставляем T₀=0,02 и для учета фиксатора нулевого порядка умножаем W(z) на , получаем:

.

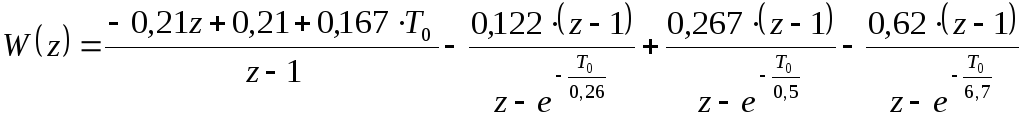Получили передаточную функцию системы, включающую и микропроцессорную систему.

6. Построение лах неизменяемой части системы

Для того чтобы получить частотную передаточную функцию, дискретной системы, нужно сделать ряд преобразований с передаточной функцией W(z) 1)  – преобразование и 2) получаем частотную передаточную функцию через псевдочастоту :

1. Получим w-преобразование нашей функции W(z), используя подстановку:

тогда

.

Разложим числитель на стандартные звенья. Для этого написана программа в электронной таблице Excel. Многочлен разложим на три звена первой степени и два звена первого и второго порядков. Критерий квадратичной ошибки получился меньше при втором разложении, значит полученная передаточная функция системы после  - преобразования:

.

2. Выразим функцию W() через псевдочастоту:

подставляем в W()

,

.

где T₀=0,02 – период дискретизации, а  – псевдочастота. Тогда частотная передаточная функция данной системы, после ряда упрощений, будет иметь следующий вид:

Теперь мы можем построить ЛАХ неизменяемой части нашей САУ.

1. Находим частоты сопряжения.

Частоты сопряжения числителя:

, .

Частоты сопряжения знаменателя:

, , .

2. Находим уровень низкочастотной части ЛАХ на вертикальной оси:

L(w)=20lgK=20lg61,95=35,84.

В соответствии с полученными частотами сопряжения, строим ЛАХ неизменяемой части, которая приведена на рис. .