Лаб3-5

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Бийский технологический институт (филиал)

федерального государственного бюджетного образовательного

учреждения высшего образования

«Алтайский государственный технический университет

им. И.И. Ползунова»

Технологический факультет

Кафедра М Методов и средств измерения и автоматизации и

Отчет защищен с оценкой

_________________________________

А.Н. Сливин

(подпись преподавателя) (инициалы, фамилия)

«____» ___________ 2018 г.

Отчет

по лабораторной работе № 3-5.

Численное интегрирование и дифференцирование. Нелинейные уравнения и системы в SciLab. Обработка экспериментальных данных.

(название лабораторной работы)

по дисциплине «Математические пакеты»

(наименование дисциплины)

ЛР 09.03.02.01.000 ОТ Т

(обозначение документа)

Студент группы ИСТ-

подпись (инициалы, фамилия)

Преподаватель доц. к.н. А.Н. Сливин

(должность, ученое звание) подпись (инициалы, фамилия)

БИЙСК 2018

Цель работы:

• Освоить различные численные алгоритмы в функциях интегрирования и дифференцирования, реализованнные в Scilab. Научиться строить двумерные и трехмерные графики;

• Рассмотреть средства SciLab для нахождения корней нелинейных уравнений и систем;

• Освоить некоторые методы обработки экспериментальных данных с помощью пакета SciLab.

Задания:

1. Вычислить интеграл тремя способами.

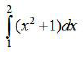
2. Вычислить значение производной функции в точке x=3.

3. Найти корни полиномов, выполнить с полиномами операции сложения, вычитания, умножения.

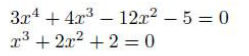
4. Решить систему уравнений.

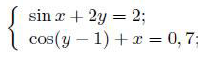
5. В результате эксперимента была определена некоторая табличная зависимость. С помощью метода наименьших квадратов определить линию регрессии, рассчитать коэффициент корреляции, подобрать функциональную зависимость заданного вида, вычислить коэффициент регрессии. Определить суммарную ошибку.

6. найти приближенное значение функции при заданном значении аргумента с помощью функции линейной интерполяции. Функция задана таблично.

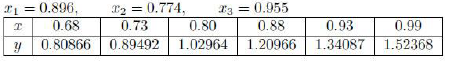
Ход работы

1. Был вычислен интеграл тремя способами (рис. 1, 2, 3, 4).

Рисунок 1 – Определение интеграла

Рисунок 2 – Интегрирование по методу трапеций

Рисунок 3 – Интегрирование по квадратуре

Рисунок 4 – Интегрирование по внешней функции

2. Было вычислено значение производной функции в точке x = 3 (рис. 5, 6).

Рисунок 5 – Приближенное дифференцирование

Рисунок 6 – Вычисление производное функции в точке

3. Для полиномов были найдены корни, а также были выполнены операции сложения, вычитания и умножения над полиномами (рис. 7, 8, 9, 10, 11, 12).

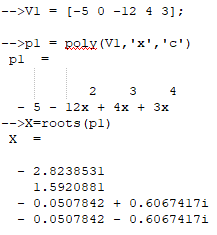
Рисунок 7 – Первый полином и его корни

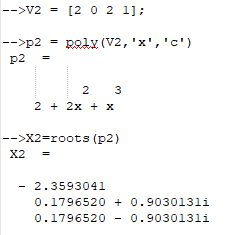
Рисунок 8 – Второй полином и его корень

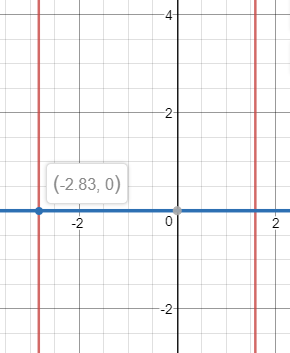
Рисунок 9 – Корни первого полинома

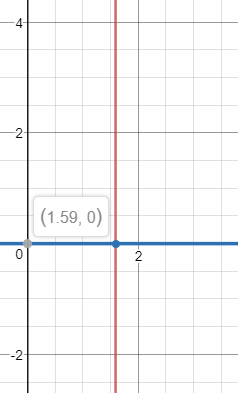
Рисунок 10 – Корни первого полинома

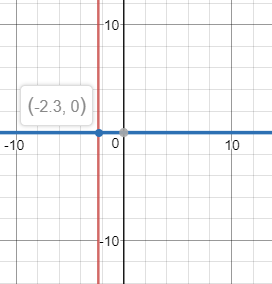
Рисунок 11 – Корень второго полинома

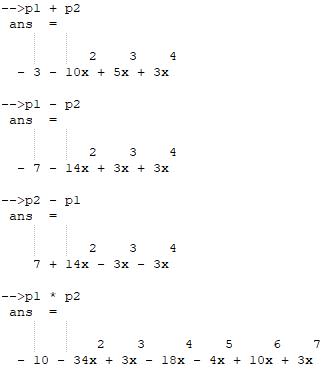
Рисунок 12 – Операции сложения, вычитания и умножения над полиномами

4. Была решена система уравнений (рис. 13, 14).

Рисунок 13 – Решение системы уравнений

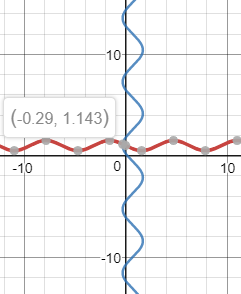
Рисунок 14 – Графическое решение системы уравнений

5. С помощью метода наименьших квадратов была определена линия регрессии, рассчитан коэффициент корреляции, подобрана функциональная зависимость заданного вида, вычислен коэффициент регрессии, а также определена суммарная ошибка (рис. 15, 16, 17, 18, 19).

Рисунок 15 – Функциональная зависимость

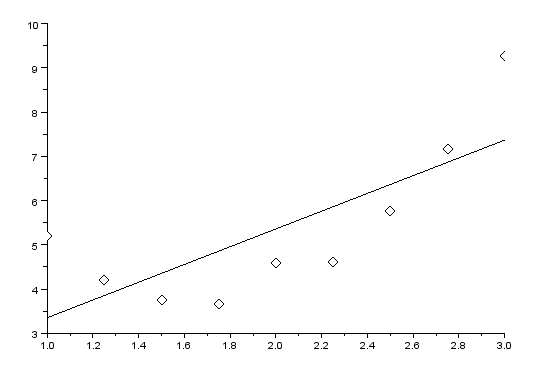
Рисунок 16 – Линия регрессии

Рисунок 17 – Коэффициент корреляции

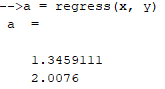
Рисунок 18 – Коэффициенты регрессии

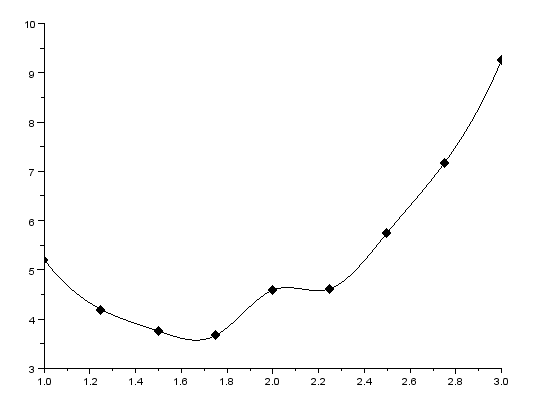
Рисунок 19 – Линейная интерполяция

6. Было найдено приближенное значение функции при заданном значении аргумента с помощью функции линейной интерполяции (рис. 20).

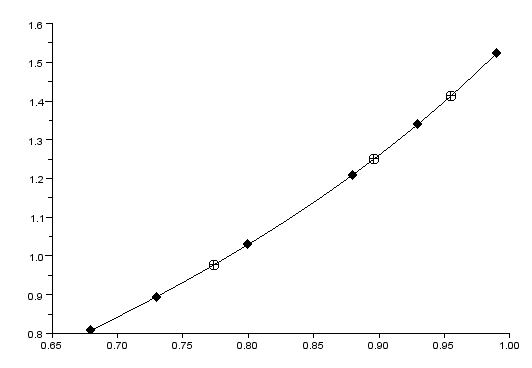
Рисунок 20 – Кубический сплайн

Вывод: в ходе выполнения лабораторной работы были получены навыки применения различных численных алгоритмов в функциях интегрирования и дифференцирования, построения двумерных и трехмерных графиков, средств нахождения корней нелинейных уравнений и систем, а также методов обработки экспериментальных данных с помощью пакета SciLab.