Методические рекомендации к лабораторным_Матпакеты

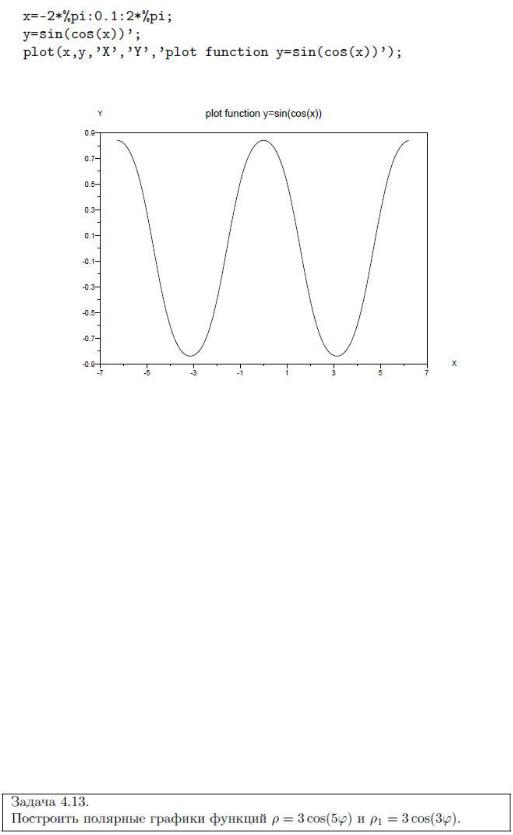
2. Построение графиков в полярной системе координат

Полярная система координат состоит из заданной фиксированной точки O – полюса, концентрических окружностей с центром в полюсе и лучей, выходящих из точки O, один из которых OX – полярная ось.

Расположение любой точки M в полярных координатах можно задать положительным числом ρ = OM (полярный радиус), и числом ρ, равным величине угла XOM (полярный угол).

В Scilab для формирования графика в полярной системе координат необходимо сформировать массивы значений полярного угла и полярного радиуса, а затем обратиться к функции polarplot:

polarplot(fi,ro)

,где fi – полярный угол, а ro – полярный радиус.

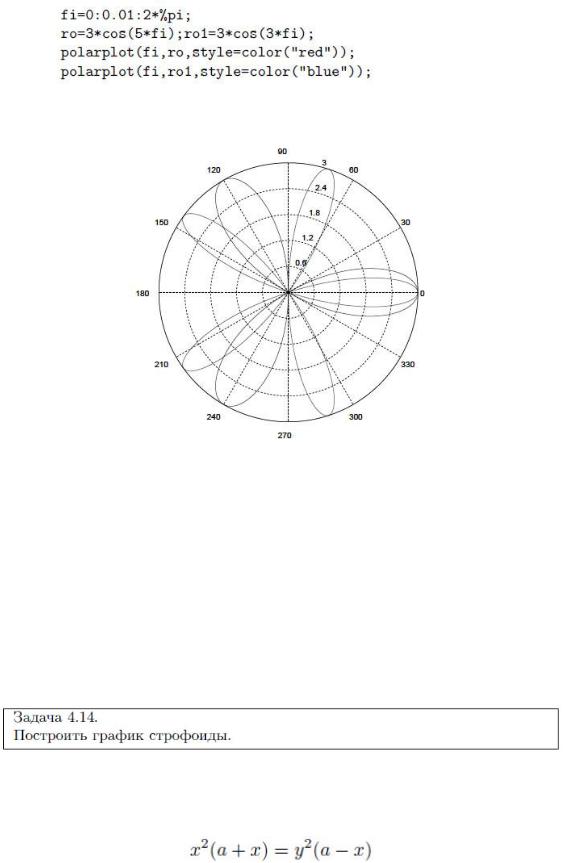
Определив диапазон и шаг изменения полярного угла, формируем массивы fi, ro. Поочередно строим заданные кривые с помощью функции polarplot, при этом для линии графика функции ro установим красный цвет, а для функции ro1 – синий.

11

3.Построение графиков функций, заданных в параметрической форме

Задание функции y(x) с помощью равенств x = f(t) и y = g(t) называют

параметрическим, а вспомогательную величину t – параметром.

Для построения графика функции, заданной параметрически, необходимо определить массив t, определить массивы x = f(t), y = g(t) и построить график функции y(x), используя функции plot(x,y) либо plot2d(x,y).

Напомним, что строфоида представляет собой алгебраическую кривую третьего порядка, которая в общем виде задается уравнением:

Представим это уравнение с помощью параметра t:

12

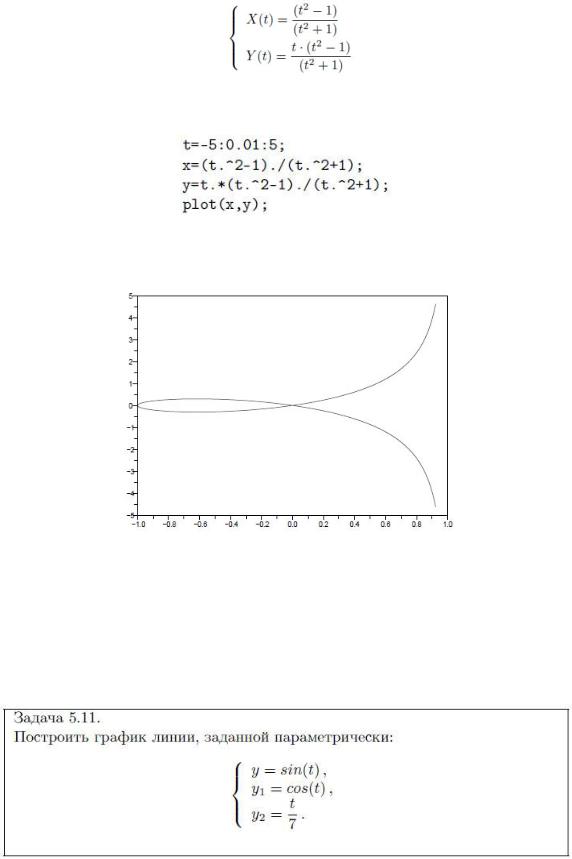
Зададим массивы t, x и y и построим график с помощью функции plot(x,y):

График строфоиды выглядит следующим образом:

Для построения параметрической кривой в трехмерном пространстве Scilab существует команда param3d:

param3d(x,y,z,)

Например:

Прежде всего, определим диапазон и шаг изменения параметра t. Затем обратимся к функции param3d, передав ей математические выражения

13

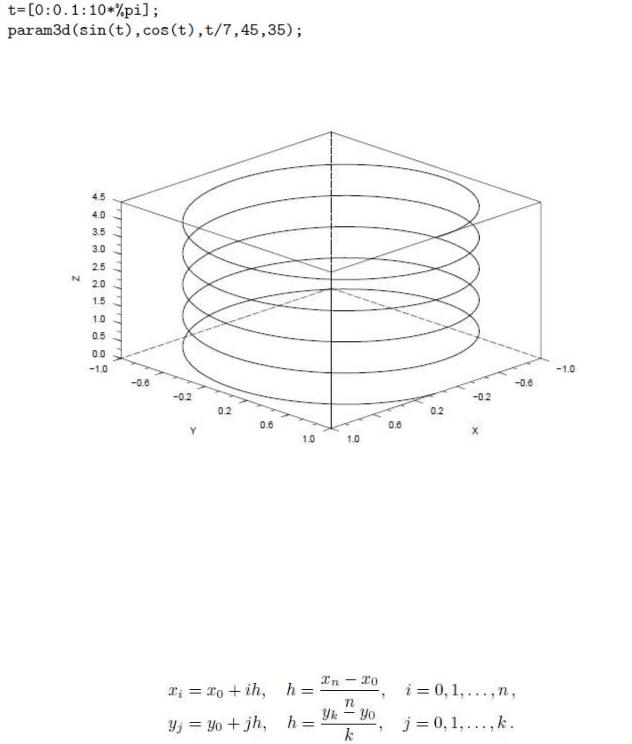
функций y, y1 и y2, а также углы в градусах, под которыми наблюдатель будет видеть формируемый график – 45 и 35.

График параметрической линии, построенный функцией param3d:

4. Построение трехмерных графиков в Scilab

К трехмерным отнесем все графики, положение каждой точки которых задается тремя величинами. В целом процесс построения графика функции вида Z(x, y) можно разделить на три этапа:

1.Создание в области построения графика прямоугольной сетки. Для этого формируются прямые линии, параллельные координатным осям xi и yj , где

2.Вычисление значений функции zij = f(xi, yj) во всех узлах сетки.

3.Обращение к функции построения трехмерных графиков.

В Scilab поверхность можно построить с помощью функций plot3d . Обращение к функциям следующее:

14

plot3d(x,y,z)

здесь x – вектор-столбец значений абсцисс; y – вектор-столбец значений ординат; z – матрица значений функции;

Прежде всего зададим массивы X и Y . Затем сформируем матрицу значений функции Zij (xi, yj), используя оператор цикла for. Здесь i – параметр цикла, который будет перебирать все значения массива X, а j – параметр цикла, который будет сопоставлять каждому значению массива X по очереди все значения массива Y .

Таким образом, сначала будут вычислены все значения функции Z при меняющемся Y (от первого до последнего значения в массиве) и первом значении массива X. Затем – при втором значении массива X и т. д. Напомним, здесь length – определяет количество элементов массива X или Y. Наконец, для построения поверхности обратимся к функции plot3d1 (аналог функции plot3d). Их отличие состоит в том, что plot3d строит поверхность и заливает ее одним цветом, а plot3d1 – поверхность, каждая ячейка которой имеет цвет, зависящий от значения функции в каждом соответствующем узле сетки.

Функция plot3d2 и является аналогом функции plot3d (не путать функции plot3d-plot3d1-plot3d2), поэтому имеет такой же синтаксис:

plot3d2(x,y,z,)

Эти функции предназначены для построения поверхности, которая задается набором граней. Т. е. если функция plot3d по входным данным сможет построить лишь отдельно стоящие друг от друга плоские грани, то plot3d2 проинтерпретирует взаимное расположение этих граней в виде цельного геометрического тела.

15

При построении графиков поверхностей, заданных параметрически – x(u, v), y(u, v)и z(u, v) – необходимо сформировать матрицы X, Y и Z одинакового размера. Для этого массивы u и v должны иметь одинаковый размер. После этого

1.Если x, y и z можно представить в виде произведения f(u) · g(v), то соответствующие X, Y и Z следует формировать в виде матричного умножения f(u) на g(v).

2.Если x, y и z можно представить в виде одной функции f(u) или g(v), то в этом случае матрицы X, Y и Z следует записывать в виде f(u) · ones(size(v)) или g(v) · ones(size(u)) соответственно.

Отметим также, что здесь linspace – функция, возвращающая массив с линейным приращением значений в заданном диапазоне. Например, u=linspace(-%pi/2,%pi/2,40) значит, что параметр u линейно изменяется в диапазоне [−2π; 2π]. Число 40 устанавливает, что массив должен содержать ровно 40 значений, по умолчанию их 100.

Построенная функцией plot3d2 сфера представлена ниже:

16

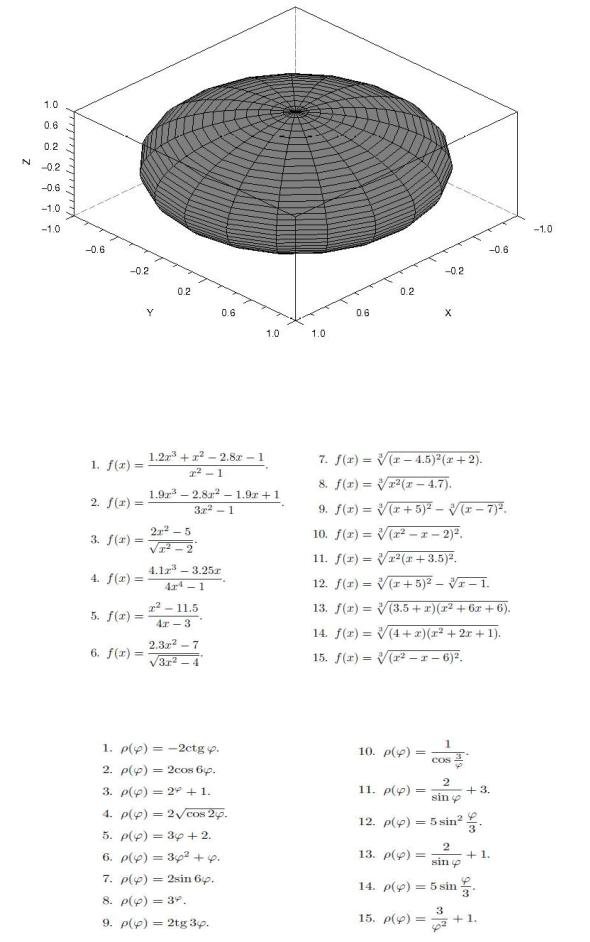
5. Задания к работе

1. Изобразите график функции f(x).

2. Изобразите график функции в полярных координатах.

17

3. Изобразить линии, заданные параметрически с помощью функции param3d.

4. Построить график, заданный системой уравнений при помощи функции plot3d2

18

ЛАБОРАТОРНАЯ РАБОТА №3

Тема: Численное интегрирование и дифференцирование

Цель работы: Цель работы: Освоить различные численные алгоритмы в функциях интегрирования и дифференцирования, реализованнные в Scilab.

1.Интегрирование по методу трапеций

В Scilab численное интегрирование по методу трапеций реализовано с помощью функции inttrap(x,y)

Эта функция вычисляет площадь фигуры под графиком функции y(x), которая описана набором точек (x, y). Параметр x является необязательным. Для функции inttrap(y) элементы вектора x принимают значения номеров элементов вектора y.

Этот интеграл легко сводится к табличному , поэтому вычислить его можно вычислить по формуле Ньютона–Лейбница:

В Scilab это будет выглядеть следующим образом:

Теперь применим для отыскания заданного определенного интеграла метод трапеций, суть которого состоит в следующем: для вычисления интеграла методом трапеций участок интегрирования разбивают на определенное количество равных отрезков, каждую из полученных криволинейных трапеций заменяют прямолинейной и вычисляют приближенное значение интеграла как сумму площадей этих трапеций.

Рассмотрим несколько вариантов решения данной задачи. В первом случае интервал интегрирования делится на отрезки с шагом 1, во втором 0.5 и в третьем 0.1. Не трудно заметить, что чем больше точек разбиения, тем точнее значение искомого интеграла:

19

Далее приведен пример использования функции inttrap с одним аргументом:

Как видим, в первом случае значение интеграла, вычисленного при помощи этой функции, неточно и совпадает со значением, полученным функцией inttrap(x,y) на интервале [5; 13] с шагом 1. Т.е. мы нашли сумму площадей восьми прямолинейных трапеций с основанием h = 1 и боковыми сторонами, заданными вектором y.

Во втором случае, при попытке увеличить точность интегрирования, значение интеграла существенно увеличивается. Дело в том, что, уменьшив шаг разбиения интервала интегрирования до 0.1, мы увеличили количество элементов векторов x и y, и применение функции inttrap(y) приведет к вычислению суммы площадей восьмидесяти трапеций с основанием h = 1 и боковыми сторонами, заданными вектором y. Таким образом, в первом и втором примерах вычисляются площади совершенно разных фигур.

2. Интегрирование по квадратуре

Методы трапеций являются частными случаями квадратурных формул Ньютона–Котеса, которые имеют вид:

где Hi –это некоторые константы, называемые постоянными Ньютона–Котеса. Если для принять n = 1, то получим метод трапеций, а при n = 2 – метод Симпсона. Эти методы называют квадратурными методами низших порядков.

Для n > 2 получают квадратурные формулы Ньютона–Котеса высших порядков. Вычислительный алгоритм квадратурных формул реализован в

20