
Методические рекомендации к лабораторным_Матпакеты
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Бийский технологический институт (филиал)
федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Алтайский государственный технический университет им. И. И. Ползунова» (БТИ АлтГТУ)
А.Н. Сливин
МАТЕМАТИЧЕСКИЕ
ПАКЕТЫ
Методические рекомендации по лабораторным работам для направления
09.03.02 – «Информационные системы и технологии»
Бийск Издательство Алтайского государственного технического
университета им. И.И.Ползунова Бийск 2015
УДК 004.65:519.85
Разработано для направления 09.03.02 – «Информационные системы и технологии»
Рецензент доц. кафедры Физики, к.т.н. Савин И.И.
Работа подготовлена на кафедре методов и средств измерений и автоматизации.
Сливин А.Н.
Математические пакеты: Методические рекомендации по проведению лабораторных занятий для студентов направления – 09.03.02 – «Информационные системы и технологии»
«Информационные системы и технологии» Сливин А.Н., – Алт. гос. техн. ун-т, БТИ. – Бийск: Алт. гос. техн. ун-та, 2015. – 15 с.
В методических рекомендациях сформулированы цели и задачи лабораторных занятий по курсу «Математические пакеты», приведены тематика лабораторных занятий, краткие теоретические сведения и примеры решения математических задач, раскрывающие сущность лабораторных занятий, даны рекомендации студентам по выполнению лабораторных работ.
УДК 004.65:519.85
ББК _________
Рассмотрено и одобрено на заседании кафедры МСИА
Протокол № ____ от |
|
2015 г |
©А.Н.Сливин, 2015
©БТИ АлтГТУ, 2015
Учебное издание
2
ЛАБОРАТОРНАЯ РАБОТА №1
Тема: Массивы и матрицы в Scilab. Решение задач линейной алгебры
Цель работы: Научиться формировать матрицы и массивы в SCILAB, выполнять действия над матрицами, решать системы линейных уравнений.
1.Введение
Для работы с множеством данных удобно использовать массивы. Например, можно создать массив для хранения числовых или символьных данных. В этом случае вместо создания переменной для хранения каждого данного достаточно создать один массив, где каждому элементу будет присвоен порядковый номер.
Таким образом, массив - множественный тип данных, состоящий из фиксированного числа элементов. Как и любой другой переменной, массиву должно быть присвоено имя.
Переменную, представляющую собой просто список данных, называют одномерным массивом, или вектором. Для доступа к данным, хранящимся в определенном элементе массива, необходимо указать имя массива и порядковый номер этого элемента, называемый индексом.
Если возникает необходимость хранения данных в виде таблиц, в формате строк и столбцов, то необходимо использовать двумерные массивы
(матрицы).
Для доступа к данным, хранящимся в таком массиве, необходимо указать имя массива и два индекса: первый должен соответствовать номеру строки, а второй - номеру столбца, в которых хранится необходимый элемент.
Значение нижней границы индексации в Scilab равно единице. Индексы могут быть только целыми положительными числами.
2.Ввод и формирование массивов и матриц
Задать одномерный массив в Scilab можно следующим образом: name=Xn:dX:Xk
где name - имя переменной, в которую будет записан сформированный массив, Xn - значение первого элемента массива, Xk - значение последнего элемента массива, dX - шаг, с помощью которого формируется каждый следующий элемент массива, т.е. значение второго элемента составит Xn+dX, третьего Xn+ dX+dX и так далее до Xk.
Если параметр dX в конструкции отсутствует, это означает, что по умолчанию он принимает значение, равное единице, т.е. каждый следующий элемент массива равен значению предыдущего плюс один:
name=Xn:Xk
3
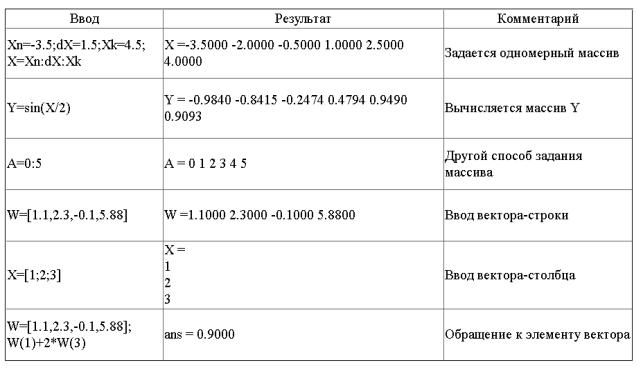
Переменную, заданную как массив, можно использовать в арифметических выражениях и в качестве аргумента математических функций.
Еще один способ задания векторов и матриц в Scilab - это их поэлементный ввод. Так, для определения вектора-строки следует ввести имя массива, а затем после знака присваивания, в квадратных скобках через пробел или запятую, перечислить элементы массива
name=[x1 x2 ... xn] или name=[x1, x2, ..., xn]
Обратиться к элементу вектора можно, указав имя массива и порядковый номер элемента в круглых скобках:
name(индекс)
Ввод элементов матрицы также осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а строки разделяются между собой точкой с запятой:
name=[x11, x12, ..., x1n; x21, x22, ..., x2n; ...; xm1, xm2, ..., xmn;]
Обратиться к элементу матрицы можно, указав после имени матрицы, в круг лых скобках через запятую, номер строки и номер столбца на пересечении кото рых элемент расположен:
name(индекс1, индекс2)
Важную роль при работе с матрицами играет знак двоеточия. Указывая его вместо индекса при обращении к массиву, можно получать доступ к группам его элементов.
4
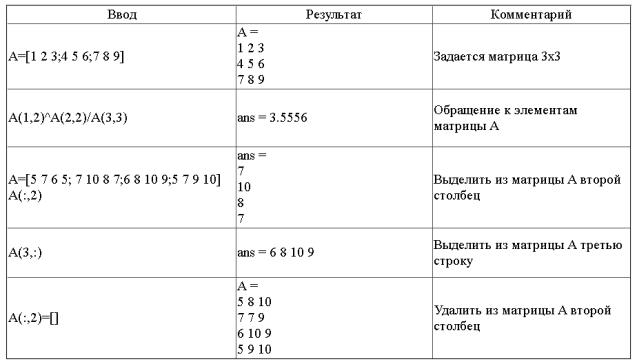
3.Действия над матрицами
Для работы с матрицами и векторами в Scilab предусмотрены следующие операции:
+ — сложение - — вычитание
Операции сложения и вычитания определены для матриц одной размерности или векторов одного типа, т.е. суммировать (вычитать) можно либо векторы-столбцы, либо векторы-строки одинаковой длины.
’ — транспонирование Если в некоторой матрице заменить строки соответствующими столбцами,
то получится транспонированная матрица.
*— матричное умножение
*— умножение на число
Операция умножения вектора на вектор определена только для векторов одинакового размера, причем один из них должен быть вектором-столбцом, а второй вектором-строкой. Матричное умножение выполняется по правилу строка на столбец и допустимо, если количество строк во второй матрице совпадает с количеством столбцов в первой. Кроме того, переместительный закон на произведение матриц не распространяется.
ˆ — возведение в степень
Возвести матрицу в n-ю степень значит умножить ее саму на себя n раз. При этом целочисленный показатель степени может быть как положительным, так и отрицательным. В первом случае выполняется алгоритм умножения матрицы на себя указанное число раз, во втором умножается на себя матрица, обратная к данной.
5

\ — левое деление Операция левого деления может быть применима для решения матричного
уравнения вида A · X = B, где
X— неизвестный вектор.
/— правое деление
Операцию правого деления используют для решения матричных уравнений вида X · A = B.
Примеры матричных операций:
Кроме того, если к некоторому заданному вектору или матрице применить математическую функцию, то результатом будет новый вектор или матрица той же размерности, но элементы будут преобразованы в соответствии с заданной функцией:
4.Решение систем линейных алгебраических уравнений
Система m уравнений с n неизвестными вида:
6

называется системой линейных алгебраических уравнений (СЛАУ),
причем xj — неизвестные, aij — коэффициенты при неизвестных, bi — свободные коэффициенты (i = 1 . .
.m, j = 1 . . . n).
Система из m линейных уравнений с n неизвестными может быть описана при помощи матриц: A · x = b, где x — вектор неизвестных, A — матрица
коэффициентов |
при |
неизвестных |
или |
матрица |
системы, |
b — вектор свободных членов системы или вектор правых частей. |
|
||||
Совокупность всех решений системы (x1, x2, . . . , xn) называется множеством решений или просто решением системы.
Существует несколько способов решения систем уравнений:
Метод Крамера
Правило Крамера заключается в следующем. Если определитель  матрицы системы из n уравнений с n неизвестными A· x = b отличен от нуля, то система имеет единственное решение x1, x2, . . . , xn, определяемое по формулам Крамера:
матрицы системы из n уравнений с n неизвестными A· x = b отличен от нуля, то система имеет единственное решение x1, x2, . . . , xn, определяемое по формулам Крамера: 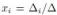 , где
, где 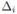 — определитель матрицы, полученной из матрицы системы A заменой i-го столбца столбцом свободных членов b.
— определитель матрицы, полученной из матрицы системы A заменой i-го столбца столбцом свободных членов b.
Метод обратной матрицы
Для системы из n линейных уравнений с n неизвестными A · x = b, при условии, что определитель матрицы A не равен нулю, единственное решение можно представить в виде x = A−1 · b.
Метод Гаусса
Решение системы линейных уравнений при помощи метода Гаусса основывается на том, что от заданной системы переходят к эквивалентной системе, которая решается проще, чем исходная система.
Метод Гаусса состоит из двух этапов. Первый этап — это прямой ход, в результате которого расширенная матрица системы путем элементарных преобразований (перестановка уравнений системы, умножение уравнений на
7

число, отличное от нуля, и сложение уравнений) приводится к ступенчатому виду. На втором этапе (обратный ход) ступенчатую матрицу преобразовывают так, чтобы в первых n столбцах получилась единичная матрица. Последний, n + 1 столбец этой матрицы содержит решение системы линейных уравнений.
5.Задания к работе
1.Решить систему линейных алгебраических уравнений тремя методами, сделать проверку.
8
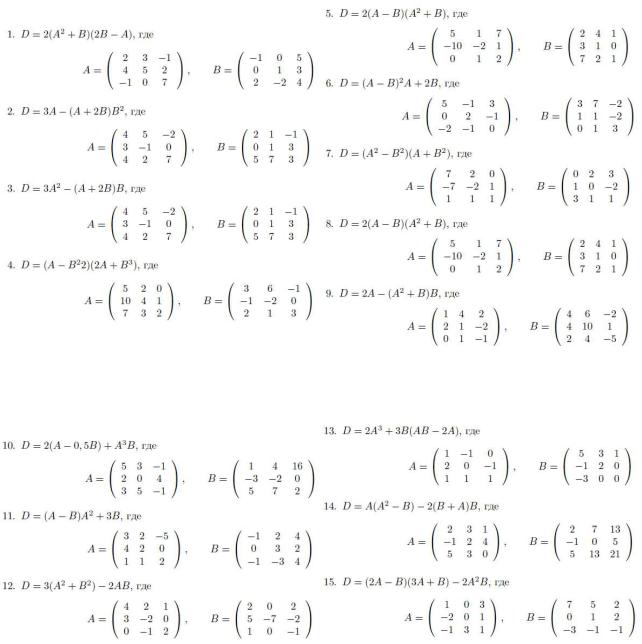
2. Если возможно, вычислить матрицу, обратную к матрице D.
9
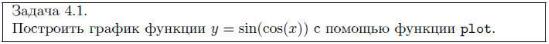
ЛАБОРАТОРНАЯ РАБОТА №2
Тема: Построение графиков в SciLab
Цель работы: Научиться строить двумерные и трехмерные графики.
1.Двумерные графики простейших функций
Рассмотрение графиков начнем с простейших функций вида y = f(x), для построения которых в Scilab существует функция plot.
Функция plot предназначена для построения графика одной функции y = f(x). Обращение к ней имеет вид:
plot(x,y,[xcap,ycap,caption])
Здесь x — массив абсцисс; y — массив ординат; xcap, ycap, caption — подписи осей и графика.
Пусть x изменяется на интервале [−2π; 2π] с шагом 0,1. Сформируем массив X. Вычисляя значение функции y = sin(cos(x)) для каждого значения массива X, создадим массив Y . Затем воспользуемся функцией plot(x,y) для построения кривой и выведем с ее же помощью подписи координатных осей ’X’, ’Y’, а также имя графика ’plot function y=sin(cos(x))’.
10
