Экспертный инженерный анализ расширения технологических функций маршрутного диагностического компьютера / 4 ВЕКТОРНО

4 ВЕКТОРНО–ЭНЕРГЕТИЧЕСКИЙ АНАЛИЗ ПАРЫ ТРЕНИЯ С ЦЕЛЬЮ КОНТРОЛЯ ИЗНОСА ДВИГАТЕЛЯ ВНУТРЕННЕГО СГОРАНИЯ АВТОМОБИЛЯ БОРТОВЫМ КОМПЬЮТЕРОМ

Векторная энергетика механических звеньев передачи энергии и мощности включает в себя статику и динамику одновременно. Это комплексный анализ механического звена передачи сигнала. Пара трения – это типичный вид канализации энергии, когда один из элементов пары передает энергию и мощность (поршень), а второй элемент пары является каналом передачи энергии и мощности (цилиндр). В чистом виде это может быть ДВС автомобиля или теплохода; нанос для перекачки жидкостей, газов, пульпы; гвоздь – дерево. Даже этих параметров достаточно, чтобы понять, что векторная энергетика пар трения определяет эффективность передачи энергии и мощности практически во всех технических системах, которыми, как известно, нужно эффективно управлять.

Анализ векторной энергетики пар трения рассматривают на примере математической модели механического гвоздика, который забивают в среду (например, в дерево), подобно тому, как поршень передвигается в цилиндре.

Расчетная формула вектора Умова энергетической реакции цилиндрической поверхности гвоздя при забивании

, ()

где R_r – радиус гвоздя, м;

– нормальный тензор (коэффициент трения) цилиндрической поверхности гвоздя;

– глубина вхождения гвоздя при одном ударе, м;

Е_дер – модуль упругости дерева, Па;

t – время удара молотком по гвоздю, с;

– максимальное расстояние, допустимое для данной породы дерева, при котором, после извлечения гвоздя, дерево восстанавливается, м.

Задача заключается в том, чтобы проанализировать на чувствительность вектор Умова энергетической реакции цилиндрической поверхности гвоздя при забивании. Диапазон измеряемого параметра плюс/минус 50% от заданного начального значения, с интервалом 10%.

Задаются следующие значения параметров:

R_r0 = 0,0026 м;

= 0,3;

= 0,0014 м;

Е_дер = 1,4 ^. 10⁵ Па;

t = 0,13 с;

= 0,0021 м.

Первым моделируемым параметром будет радиус гвоздя (R_r). Начальное значение этого параметра будет R_r0 = 0,0026 м.

Шаг измеряемого параметра

, () где 0,5 – диапазон значений (плюс/минус 50%);

5 – число точек;

R_r – радиус гвоздя.

м.

м;

м;

м;

м;

м;

м;

м;

м;

м;

м.

Полученные значения подставляют в расчетную формулу, при этом значения остальных параметров остаются неизменными

;

;

;

;

;

;

;

;

;

;

.

По полученным данным строят график зависимости вектора Умова от изменяемого параметра (рисунок ).

Вектор Умова энергетической реакции цилиндрической поверхности гвоздя прямо пропорционален изменению радиуса гвоздя. Чем больше радиус гвоздя, тем больше затрачивается энергии на один квадратный метр и, наоборот, чем тоньше гвоздик, тем меньше энергетическая реакция цилиндрической поверхности при забивании гвоздя.

Рисунок – Зависимость вектора Умова энергетической реакции цилиндрической поверхности от изменения радиуса гвоздя

Следующим моделируемым параметром будет нормальный тензор (коэффициент трения) цилиндрической поверхности гвоздя (). Начальное значение этого параметра будет = 0,3.

Шаг измеряемого параметра

, ()

где 0,5 – диапазон значений (плюс/минус 50%);

5 – число точек;

– нормальный тензор цилиндрической поверхности гвоздя.

.

;

;

;

;

;

;

;

;

;

.

Полученные значения подставляют в расчетную формулу, при этом значения остальных параметров остаются неизменными

;

;

;

;

;

;

;

;

;

;

.

По полученным данным строят график зависимости вектора Умова от изменяемого параметра (рисунок ).

Рисунок– Зависимость вектора Умова энергетической реакции

цилиндрической поверхности от изменения нормального тензора цилиндрической поверхности гвоздя

Вектор Умова энергетической реакции цилиндрической поверхности гвоздя прямо пропорционален изменению нормального тензора цилиндрической поверхности. Чем выше нормальный тензор цилиндрической поверхности. Чем выше нормальный тензор цилиндрической поверхности, тем выше энергетическая реакция при забивании гвоздя, и соответственно, чем меньше коэффициент трения, тем меньше энергетическая реакция вектора Умова на один квадратный метр.

Следующим моделируемым параметром будет глубина вхождения гвоздя при одном ударе (). Начальное значение этого параметра будет = 0,0014 м.

Шаг измеряемого параметра

, () где 0,5 – диапазон значений (плюс/минус 50%);

5 – число точек;

– глубина вхождения гвоздя при одном ударе.

м.

м;

м;

м;

м;

м;

м;

м;

м;

м;

м.

Полученные значения подставляют в расчетную формулу , при этом значения остальных параметров остаются неизменными

;

;

;

;

;

;

;

;

;

;

.

По полученным данным строят график зависимости вектора Умова от изменяемого параметра (рисунок).

Рисунок – Зависимость вектора Умова энергетической реакции цилиндрической поверхности от изменения глубины вхождения гвоздя при одном ударе

Вектор Умова энергетической реакции цилиндрической поверхности гвоздя прямо пропорционален изменению глубины вхождения гвоздя при одном ударе. При увеличении глубины вхождения гвоздя, нужно затратить больше энергии на один квадратный метр, соответственно для того, чтобы забить гвоздь на небольшую глубину энергии затрачивается меньше на один квадратный метр.

Следующим моделируемым параметром будет модуль упругости дерева (Е_дер). Начальное значение этого параметра будет Е_дер = 1,4 ^. 10⁵ Па.

Шаг измеряемого параметра

, ()

где 0,5 – диапазон значений (плюс/минус 50%);

5 – число точек;

Е_дер – модуль упругости дерева.

Па.

Па;

Па;

Па;

Па;

Па;

Па;

Па;

Па;

Па;

Па.

Полученные значения подставляют в расчетную формулу , при этом значения остальных параметров остаются неизменными

;

;

;

;

;

;

;

;

;

;

.

По полученным данным строят график зависимости вектора Умова от изменяе

мого параметра (рисунок).

Рисунок – Зависимость вектора Умова энергетической реакции цилиндрической поверхности от изменения модуля упругости дерева

Вектор Умова энергетической реакции цилиндрической поверхности гвоздя при забивании прямо пропорционален модулю упругости дерева. Чем выше модуль упругости, то есть крепче дерево, тем больше энергетическая реакция вектора Умова, и, наоборот, для того чтобы забить гвоздь в мягкую породу дерева, энергетическая реакция цилиндрической поверхности гвоздя меньше на один квадратный метр.

Следующим моделируемым параметром будет время удара молотком по гвоздю (t). Начальное значение этого параметра будет t₀ = 0,13 с.

Шаг измеряемого параметра

, () где 0,5 – диапазон значений (плюс/минус 50%);

5 – число точек;

t – время удара молотком по гвоздю.

с.

с;

с;

с;

с;

с;

с;

с;

с;

с;

с.

Полученные значения подставляют в расчетную формулу 4, при этом значения остальных параметров остаются неизменными

;

;

;

;

;

;

;

;

;

;

.

По полученным данным строят график зависимости вектора Умова от изменяемого параметра (рисунок).

Рисунок Зависимость вектора Умова энергетической реакции

цилиндрической поверхности от изменения времени удара молотком

по гвоздю

Вектор Умова энергетической реакции цилиндрической поверхности гвоздя обратно пропорционален изменению времени удара молотком по гвоздю. При уменьшении времени удара молотком по гвоздю, затрачивается больше энергии

на один квадратный метр, энергетическая реакция увеличивается.

Определяют чувствительность зависимости вектора Умова от изменениявремени удара молотком по гвоздю. Для этого рассчитывают коэффициент крутизны.

Рассматриваются максимальные точки А₁ и А₂ (рисунок) и рассчитывается коэффициент к₁

, ()

где у_А1, у_А2, х_А1, х_А2 – значения максимальных соседних точек вектора Умова ивремени удара молотком по гвоздю.

Рассматриваются минимальные точки В₁ и В₂ (рисунок и рассчитывается коэффициент к₂

, ()

где у_В1, у_В2, х_В1, х_В2 –значения минимальных соседних точек вектора Умова и времени удара молотком по гвоздю.

Рисунок 30 – Расчет коэффициента крутизны изменения вектора Умова от изменения времени удара молотком по гвоздю

Из расчетов видно, что коэффициент к₁ максимальный. Значит, реакция вектора Умова на изменение времени удара молотком по гвоздю на данном участке наиболее чувствительна.

Следующим моделируемым параметром будет максимальное расстояние, допустимое для данной породы дерева, при котором, после извлечение гвоздя, дерево восстанавливается. Начальное значение этого параметра будет = 0,0021м.

Шаг измеряемого параметра

() м.

м;

м;

м;

м;

м;

м;

м;

м;

м;

м.

Полученные значения подставляют в расчетную формулу , при этом значения остальных параметров остаются неизменными

;

;

;

;

;

;

;

;

;

;

.

По полученным данным строят график зависимости вектора Умова от изменяемого параметра (рисунок).

Рисунок– Зависимость вектора Умова энергетической реакции

цилиндической поверхности от изменения максимального

расстояния, которое допустимо для данной породы дерева

Вектор Умова энергетической реакции цилиндрической поверхности гвоздя обратно пропорционален изменению максимального расстояния, допустимого для данной породы дерева, при котором после извлечения гвоздя, дерево восстанавливается. Данная порода дерева восстанавливается на 0,0021 м, при этом затрачивается 560 Вт на один квадратный метр. При уменьшении максимального расстояния допустимого для восстановления дерева, увеличивается энергетическая реакция цилиндрической поверхности, а при увеличении максимального расстояния, энергетическая реакция уменьшается.

Определяют чувствительность зависимости вектора Умова от изменения максимального расстояния, допустимого для данной породы дерева. Для этого рассчитывают коэффициент крутизны

Рассматриваются максимальные точки А₁ и А₂ (рисунок) и рассчитывается коэффициент к₁

, ()

где у_А1, у_А2, х_А1, х_А2 – значения максимальных соседних точек вектора Умова и времени удара молотком по гвоздю.

Рассматриваются минимальные точки В₁ и В₂ (рисунок) и рассчитывается коэффициент к₂

, ()

где у_В1, у_В2, х_В1, х_В2 – значения минимальных соседних точек вектора Умова и времени удара молотком по гвоздю.

.

Из расчетов видно, что коэффициент к₁ максимальный. Значит, реакция вектора Умова на изменение максимального расстояния допустимого для данной породы дерева, на данном участке наиболее чувствительна.

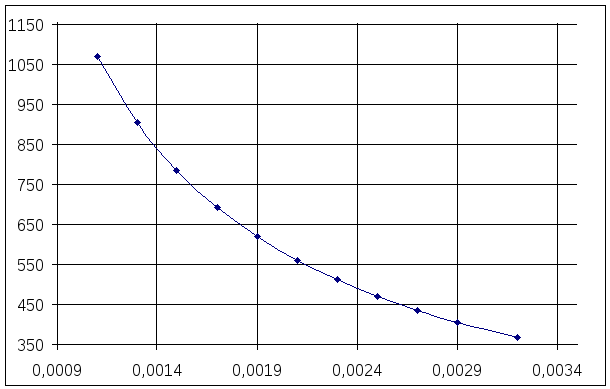
Рисунок – Расчет коэффициента крутизны изменения вектора Умова от изменения максимального расстояния допустимого для дан ной породы дерева на восстановление

Рассчитав и проанализировав все параметры, рассмотренные выше, можно сделать следующие выводы.

Рассмотрев структуру дерева, ее модуль упругости, понятно то, что в более мягкую породу дерева гвоздь вбить, конечно же, легче. Но если брать такое дерево, при котором энергетическая реакция вектора Умова будет минимальной, при этом возрастает такой параметр как максимальное расстояние допустимое для восстановления дерева .

Если рассмотреть этот параметр подробнее (рисунок), то из расчетов и графиков видно, что при уменьшении максимального расстояния допустимого на восстановление дерева на 50% – вектор Умова увеличивается на 50%, а при увеличении максимального расстояния допустимого на восстановление на 50% – вектор Умова уменьшается всего лишь на 33%. И далее, при все большем увеличении , интервалы между изменениями вектора Умова будут уменьшаться незначительно. Отсюда видно, что далее увеличивать максимальное расстояние, допустимое для данной породы на восстановление дерева, будет бессмысленным, так как энергетическая реакция вектора Умова будет уменьшаться очень медленно, что будет не эффективно для работы.

Энергетическую реакцию цилиндрической поверхности можно снизить уменьшением коэффициента трения (нормального тензора цилиндрической поверхности), также глубины вхождения гвоздя при одном ударе, так как эти параметры прямо пропорциональны. Но при этом возрастает такой параметр как увеличении времени одного удара молотком по гвоздю (t).

Если рассмотреть этот параметр подробнее,то из расчетов и графиков видно, что, увеличивая время одного удара молотком на 50%, вектор Умова при этом уменьшается всего лишь на 33%. Дальнейшее увеличение времени одного удара молотком по гвоздю будет бессмысленно, так как вектор Умова при этом уменьшается незначительно.