Экспертный инженерный анализ расширения технологических функций маршрутного диагностического компьютера / 3 ВЕКТОРНО

3 ВЕКТОРНО–ЭНЕРГЕТИЧЕСКИЙ АНАЛИЗ ПРУЖИНЫ ПЕРЕДНЕЙ ПОДВЕСКИ С ЦЕЛЬЮ КОНТРОЛЯ АКТИВНОЙ ПОДВЕСКИ

АВТОМОБИЛЯ БОРТОВЫМ КОМПЬЮТЕРОМ

Векторно-энергетический анализ элементов систем управления базируется на основополагающих работах классиков по векторной энергетике. Суть его заключается в том, что рассматривается миграция вектора Умова , [Вт/м²] по всем участкам конструкции того или иного элемента системы управления. Механическая пружина является одним из наиболее часто используемых приборных элементов.

Пружина и амортизатор при проектировании автомобиля подбираются, не зависимо друг от друга. Параметры пружины выбираются исходя из нагрузок на ось, чтобы обеспечить оптимальный диапазон собственных частот колебаний системы – в районе 1 Гц, а также с учетом параметров другой оси и с учетом обеспечения требуемой угловой жесткости для управляемости и устойчивости.

Рисунок 1 – Расчетная схема пружины амортизатора

Данные, необходимые для расчета:

D – диаметр пружины, м;

d – диаметр материала проволоки пружины, м;

– угол навивки пружины, рад;

n – число витков пружины;

Е – модуль упругости материала проволоки пружины, Па;

t – время действия силы на пружину, с;

J – момент инерции поперечного сечения проволоки пружины, м⁴;

– перемещение пружины под воздействием сжимающего усилия, м.

Реактивный вектор Умова при сжатии пружины

, (1)

Формула (1) показывает поведение вектора Умова при варьировании каждого конструктивного параметра. Но для оценки чувствительности полученного решения при изменении каждого параметра проводят, например, «плюс/минус» пятипроцентное изменение каждого из параметров от начального значения.

Задают конкретные значения параметров:

D = 0,15 м;

n = 8;

d = 0,0024 м;

Н = 0,03 м;

= 0,523 рад;

G = 0,71^.10¹¹ Па;

t = 2 с;

J = 1,659^.10^-9 м⁴.

Методика моделирования будет следующей: один из параметров изменяем на +- 5 % от заданного значения (начальное значение - за­данный номинал, 2 точки влево от него и 2 точки вправо от него), при этом остальные оставляем постоянными на заданном уровне.

Первым девиантным аргументом является величина ∆H = 0,003 м, шаг девиации равен 10% от 0,003м, получаем 0,0003 м, делим его на 5 , получаем 0,00008 м, следовательно, аргументные точки моделирования будут следующими:

Аргументные точки моделирования

м;

м;

м;

м;

м.

Каждый аргумент подставляют в формулу 1 для получения пяти значений вектора Умова

По полученным данным строят график зависимости вектора Умова от деформации пружины (рисунок).

Рисунок - Девиация вектора Умова при изменении деформации пружины ∆H на ±5%

При изменении Н на 10% (± 5% от ) вектор Умова изменяется на 8,33%.

Следующим варьируемым параметром будет момент инерции геометрического сечения проволоки пружины (J). Начальное значение этого параметра будет составлять J₀ = 1,659^.10^-12 м⁴.

Аргументные точки моделирования

м⁴;

м⁴;

м⁴;

м⁴;

м⁴.

Каждый аргумент подставляют в формулу 1 для получения пяти значений вектора Умова

По полученным данным строят график зависимости вектора Умова от момента инерции геометрического сечения проволоки (рисунок ).

При возрастании момента инерции геометрического сечения проволоки пружины, вектор Умова также растет.

рИСУНОК – Девиация вектора Умова при изменении геометрического моента инерции поперечного сечения проволоки пружины

Следующим варьируемым параметром будет модуль упругости материала пружины (G). Начальное значение этого параметра будет составлять G = 0,71 ^.10¹¹ Па. Опять берется десяти процентный диапазон из пяти точек.

Аргументные точки моделирования

Па;

Па;

Па;

Па;

Па.

Каждый аргумент подставляют в формулу 1 для получения пяти значений вектора Умова

полученным данным строят график зависимости вектора Умова от модуля упругости материала пружины (рисунок ).

Рисунок – Девиация вектора Умова при изменении модуля упругости

материала пружины передней подвески

При увеличении вектора Умова улучшается качество пружины (растет упругость). С изменением модуля упругости материала пружины G на десять процентов вектор Умова изменяется на 1,5%.

Следующим варьируемым параметром будет угол навивки пружины (). Начальное значение этого параметра будет составлять = 0,262 рад.

Аргументные точки моделирования

;

;

;

;

.

Каждый аргумент подставляют в формулу 1 для получения пяти значений вектора Умова

По полученным данным строят график зависимости вектора Умова от угла навивки пружины (рисунок ).

Рисунок – Девиация вектора Умова при изменении угла навивки

пружины передней подвески

Вектор Умова зависит от угла навивки пружины, в данном случае угол увеличивается, а вектор Умова уменьшается. С изменением угла навивки пружины на 10% вектор Умова изменяется на 12,5%.

Следующим варьируемым параметром будет число витков пружины (n). Существует повальное стремление автолюбителей приподнять или опустить задок своего автомобиля. Самый распространенный вариант – это обрезка пружин, чего делать нельзя, так как обязательно должен быть опорный виток. Наличие этого витка обеспечивает правильное складывание и работу пружины, иначе пружина будет ломаться. Лучший вариант – это заказать пружину с необходимым количеством витков у производителя. Начальное значение этого параметра будет составлять n = 8.

Шаг девиации будет равен: 8 ^. 10% : 5 = 0,16.

Аргументные точки моделирования

;

;

;

;

.

Каждый аргумент подставляют в формулу 1 для получения пяти значений вектора Умова

По полученным данным строят график зависимости вектора Умова от количества витков (рисунок ). При возрастании числа витков в пружине вектор Умова уменьшается, что приводит к ухудшению упругости пружины. С изменением числа витков пружины на 10% вектор Умова изменяется на 37,4%.

Рисунок – Девиация вектора Умова при изменении числа витков

пружины передней подвески

Следующим варьируемым параметром будет внешний диаметр пружины (D). Начальное значение этого параметра будет составлять D = 0,15 м.

Шаг девиации будет равен: 0,15 ^. 10% : 5 = 0,003 м.

Аргументные точки моделирования

м;

м;

м;

м;

м.

Каждый аргумент подставляют в формулу 1 для получения значений

;

;

;

;

.

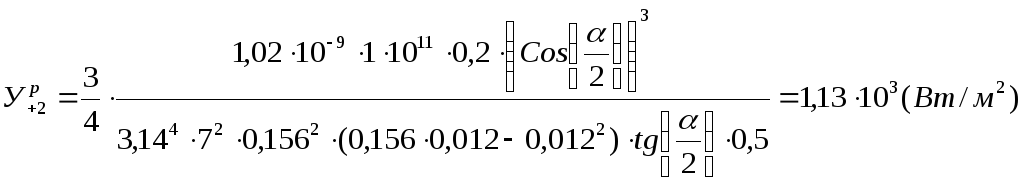По полученным данным строят график зависимости вектора Умова от диаметра пружины (рисунок ).

Рисунок – Девиация вектора Умова при изменении диаметра пружины

Диаметр пружины увеличивается, а вектор Умова уменьшается, что приводит к ухудшению качества пружины. С изменением диаметра пружины на 10% вектор Умова изменяется на 28,05%.

Следующим варьируемым параметром будет диаметр проволоки пружины (d). Начальное значение этого параметра будет составлять d = 0,012 м.

Шаг девиации будет равен: 0,012 ^. 10% : 5 = 0,00024 м.

Аргументные точки моделирования

м;

м;

м;

м;

м.

Каждый аргумент подставляют в формулу 1 для получения пяти значений вектора Умова

;

;

;

;

.

По полученным данным строят график зависимости вектора Умова от диаметра проволоки пружины (рисунок 22).

Рисунок– Девиация вектора Умова при изменении диаметра проволоки

При увеличении диаметра проволоки пружины вектор Умова уменьшается, при этом ухудшается качество пружины. С изменением диаметра пружины на 10% вектор Умова изменяется на 6,3%.

Следующим варьируемым параметром будет время воздействия силы на пружину (t). Начальное значение этого параметра будет составлять t = 2 с.

Шаг девиации будет равен: 2 ^. 10% : 5 = 0,04 с.

Берем 10%-ный диапазон из 5 точек.

Подставляем каждый аргумент в формулу (1) и получаем 5 значений вектора Умова.

По полученным данным строят график зависимости вектора Умова от времени воздействия силы на пружину (рисунок ).

Рисунок – Девиация вектора Умова при изменении времени воздействия силы на пружину

При увеличении времени действия на пружину вектор Умова уменьшается.

Чем меньше вектор Умова, тем дольше по времени пружина возвращается в первоначальное положение. С изменением времени действия на пружину на десять процентов вектор Умова изменяется на 8,3%.

Проведенное многопараметрическое моделирование позволяет дать инженерные рекомендации для проектирования пружины передней подвески при заданных начальных значениях параметров, взятые по максимальному значению вектора Умова: D = 0,15 м; n = 8; d = 0,0024 м; Н = 0,03 м; = 0,523 рад; G = 0,71^.10¹¹ Па; t = 2 с; J = 1,659^.10^-9 м⁴.

Эти параметры должны обеспечивать наиболее долговечные эксплуатацию пружины как элемента систем управления автомобилями, машиностроительными станками, элементами приборов.