5 Графическое изображение магнитного поля
Существует несколько основных способов графического изображения магнитных (и электрических) полей. Так как электромагнитное поле в общем случае является функцией координат и времени, то, для магнитного поля, магнитная индукция зависит от четырех переменных. Кроме того, магнитная индукция является векторной величиной и в каждой точке пространства имеет свое направление и величину.
Изображение магнитного поля с помощью графиков: это зависимости индукции от координат, времени. В этом случае строят отдельные графики (точнее, их семейства) для разных координат. Если поле двумерное, или рассматривается только одна плоскость трехмерного пространства, то возможно построение трехмерного графика, где по оси z откладывается величина индукции магнитного поля. Такие графики строят для каждого момента времени.
Построение графиков не дает наглядной картины поля, поэтому чаще используют построение магнитных силовых линий. Силовые линии - замкнутые сами на себя воображаемые кривые, касательные к которым в каждой точке показывают направление вектора магнитной индукции, а густота линий – величину магнитной индукции. Построение силовых линий возможно как для двумерного, так и для трехмерного случая. Для каждого момента времени строится отдельная картина силовых линий.
В последнее время все большее распространение получил метод цветного отображения магнитного поля. Каждая точка пространства (плоскости) получает свой цвет в зависимости от величины (модуля) магнитной индукции. Например, более сильное поле закрашивается в красный цвет, слабое – в синий с соответствующим переходом и промежуточными цветами. Направление вектора магнитной индукции в этом случае можно указывать отрезками прямых или силовыми линиями. Этот метод является наиболее точным для графического изображения поля. Как и в предыдущих случаях строится картина для каждого момента времени. Современные средства мультимедиа позволяют при помощи ЭВМ составить из отдельных изображений полную картину в виде анимации, как в реальном масштабе времени, так и растянутом (сжатом).
6 Расчет управляющего поля катушек
В составе ГЭПП имеются 2 катушки, питаемые переменным током с частотой 1000 Гц. Они имеют общую среднюю точку и включены согласно. Средняя точка подключена к усилителю, поэтому ток, ответвляемый из средней точки, мал по сравнению с током в катушке. Следовательно, можно считать, что через обе катушки протекает одинаковый ток.
Магнитное поле согласно включенных катушек складывается, поэтому при расчете две катушки будем учитывать как одну.
На рисунке 4 приведена конфигурация и расположение катушек.
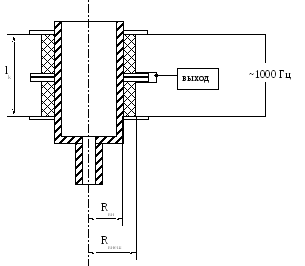
Рисунок 4 – Конфигурация и расположение катушек
Катушки имеют осевую симметрию, поэтому для расчета целесообразно использовать цилиндрическую систему координат. Изобразим схематически катушку в выбранной системе координат (рисунок 5).
Рисунок 5 – Цилиндрическая система координат
Начало координат располагается в верхней части катушек. Система координат обозначена синим цветом и имеет 3 координаты: r, z, α, то есть радиальную составляющую, осевую составляющую и угол α. Точка M с координатами M(RM, ZM, αM) – любая точка внутри катушки, то есть точка источника магнитного поля. Точка Q(RQ, ZQ, αQ) – любая точка вне катушки, то есть точка наблюдения.
Катушка состоит из множества витков, поля которых складываются согласно принципу суперпозиции. Таким образом, для расчета поля катушки следует рассчитать поле одного витка. При намотке катушки ее витки получают некоторый наклон. Расчет поля такой катушки /4, с.350/ показывает, что магнитное поле приобретает наклон с тем же углом. Но, так как управляющая катушка состоит из нескольких слоев, а наклон каждого слоя противоположен наклону предыдущего, то каждые два слоя компенсируют наклон друг друга. При большом числе слоев и малом, по сравнению с диаметром катушки, диаметре провода, что применимо и к нашему случаю, наклон поля катушки либо совсем отсутствует, либо пренебрежимо мал. Поэтому в дальнейших расчетах будем предполагать, что витки образованы концентрическими кольцами и наклон поля отсутствует.