4.5 Расчет передаточной функции системы автоматического

регулирования. Определение устойчивости системы автоматического

регулирования

Структурную схему на основе передаточных функций полученных ранее.

Рисунок 15 – Функциональная схема

Передаточная функция микропроцессора имеет вид:

Передаточная функция электрогидроусилителя типа "сопло–магнитожид­костная заслонка" имеет вид

Передаточная функция гидроцилиндра имеет вид:

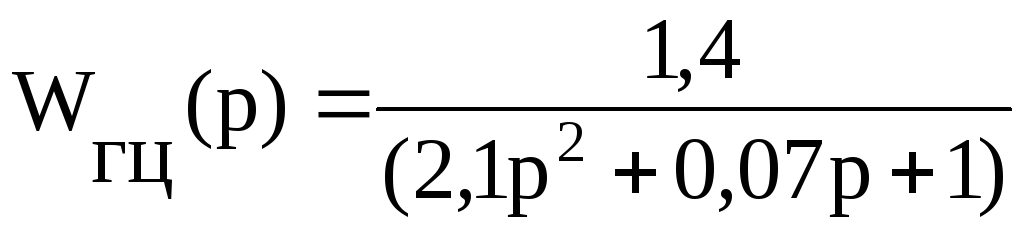
Передаточная функция датчика перемещения имеет вид:

Выделим в функциональной схеме изменяемую и неизменяемую части. Изменяемая часть состоит из микропроцессора, АЦП и ЦАП. Неизменяемая часть состоит из гидроцилиндра W_ГЦ, электрогидроусилителя сопло–магнитожидкосная заслонки W_ЭГУ и датчика перемещения W_ДП.

Передаточная функция замкнутой системы имеет вид:

Передаточная функция разомкнутой системы имеет вид:

Оценим устойчивость системы по критерию Найквиста. Для этого рассмотрим разомкнутую систему. Для того, чтобы система была устойчивой в замкнутом состоянии, необходимо и достаточно, чтобы кривая АФЧХ разомкнутой системы при изменении частоты ω от 0 до  не охватывала точку (-1, j0).

Заменим в передаточной функции разомкнутой системы р на jω.

Найдем мнимую и действительную части:

Тогда АФЧХ представлена на рисунке 11.

Рисунок 11 – АФЧХ разомкнутой системы

Условие устойчивости Найквиста выполняется (кривая не охватывает точку (-1, j0)), следовательно, система устойчива.

Для наглядного отображения свойств рассматриваемой системы построим переходный процесс, воспользовавшись обратным преобразованием Лапласа от передаточной функции замкнутой системы.

Рисунок 12 – Переходный процесс нескорректированной системы

По графику переходного процесса (рисунок 12) определим показатели качества системы:

а) Время регулирования (время переходного процесса) - время, за которое система приходит к установившемуся значению с некоторой долей погрешности. Обычно она составляет 5% (пятипроцентная трубка). Приблизительно время регулирования составляет 2,9·10⁴ (с). t_p = 2,9·10⁴

б) Перерегулирование отражает в процентах максимальное отклонение от установившегося значения.

Максимальное значение отсутствует, тогда перерегулирование:

По характеру переходного процесса можно судить об устойчивости системы: характеристика устойчивая монотонно возрастающая.

4.6 Построение логарифмической амплитудно-частотной и фазо-частотной характеристик системы и их анализ

Рисунок 13 – ЛАЧХ системы

Рисунок 14 – ЛФЧХ системы

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) и логарифмическая фазо–частотная характеристика (ЛФЧХ) определяются по передаточной функции разомкнутой системы следующим образом:

где U(ω), V(ω) – действительные и мнимые части передаточной функции.

Для найденных раннее выражений имеем ЛАЧХ и ЛФЧХ, представленные на рисунках 13 и 14 соответственно.

По построенным характеристикам определим запасы по фазе и амплитуде. Запас по амплитуде определяется следующим образом. Находится частота при которой ЛФЧХ первый раз пересекает прямую со значением -180⁰, в этой частоте проводится вертикальная прямая до пересечения с ЛАЧХ. Расстояние от этой точки пересечения до оси составляет запас устойчивости по амплитуде в децибелах. В нашем случае он составляет 82 дб. Кроме этого можно сделать вывод об устойчивости системы. ЛАЧХ в этой точке пересечения должна находиться ниже оси. Если она находится выше, то система неустойчива, пересекает ось в этой точке – на границе устойчивости.

Запас устойчивости по фазе определяется следующим образом. Определяется частота при которой ЛАЧХ пересекает ось (0 децибел). При этой частоте проводится вертикальная прямая вниз до пересечения с ЛФЧХ. Расстояние от точки пересечения до прямой -180⁰ составит запас по фазе в градусах. В нашем случае ЛАЧХ не пересекает ось 0, следовательно, судить о запасе по фазе нельзя.