§ 4.5. Функциональные потенциометрические датчики

Для получения выходного сигнала, изменяющегося по определен­ному закону, применяют функциональные потенциометрические датчики. В этих датчиках зависимость сопротивления обмотки от перемещения движка является нелинейной. Требуемая нелиней­ность обеспечивается различными способами: изменением профиля

каркаса; изменением материала или размера провода; изменением

I шага намотки или длины витка.

1 Функциональные потенциометрические датчики нашли приме-

1 нение в автоматических вычислительных системах. Например, в ав-

I тематических навигационных системах самолетов и кораблей ис-

I пользуются электромеханические счетно-решающие устройства, вы-

I полняющие операции умножения скорости на синус или косинус

1 курсового угла. С помощью функциональных датчиков может быть

I скомпенсирована исходная нелинейность первичного чувствитель-

I ного элемента. Например, в баке сложного профиля уровень горю-

I чего не связан линейно с объемом. С помощью функционального

I датчика можно обеспечить линейную зависимость между выходным

I сигналом датчика и количеством горючего в баке.

I Чаще всего получение необходимой функциональной зависимо-

I сти обеспечивается подбором определенного профиля каркаса по-

| тенциометра. Конструкция так называемого «профильного» потен-

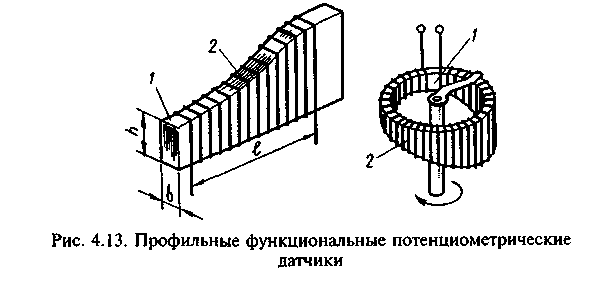
I циометрического датчика показана на рис. 4.13. Изоляционный

1 каркас 1 имеет небольшую постоянную толщину Ь, а высота его Л

I изменяется по длине намотки /. На каркас наматывается проволока

I 2с высоким удельным сопротивлением. При входных сигналах в

I виде угловых перемещений каркас с непрерывной обмоткой изгиба-

I ют в цилиндр. Напряжение питания подается на концы обмотки.

I Выходное напряжение U_eax=f(x), функционально зависящее от пе-

I ремещения движка х, снимается между одним из концов обмотки и

движком (щеткой).

Вид функциональной зависимости U_BbK =f(x) определяется фор- \ мой выреза каркаса потенциометра, т. е. зависимостью его профиля • (конкретнее — высоты Л) от перемещения движка х. Если намотка

проволоки на каркас выполнена с постоянным шагом, т. е. равно-

мерно, и потенциометр работает в режиме, близком к холостому ходу (Л„ » R; р -»оо), то высота каркаса определяется по формуле

где / — длина намотки потенциометра; q — сечение провода; R — общее сопротивление намотки; U — напряжение питания; ш— чис­ло витков; р — удельное сопротивление материала провода; b — толщина каркаса.

Анализ этого уравнения показывает, что форма профиля карка­са зависит от производной функции, воспроизводимой при помощи данного датчика. Для определения нужного профиля каркаса надо продифференцировать по перемещению х заданную зависимость выходного напряжения.

Рассмотрим несколько примеров расчета профиля потенциомет-рических датчиков.

Пример 4.1. Определить форму профиля каркаса линейного по­тенциометра с выходной характеристикой U_eta = ex.

Решение. Производная выходного напряжения по перемеще­нию df/_Bblx/dx = c. Высота каркаса по уравнению (4.10) равна h = kc - b. Все величины, входящие в это выражение, постоянны, значит, и высота каркаса h для линейного потенциометра должна быть постоянной.

Пример 4.2. Определить форму профиля каркаса функционального потенциометра с выходной характеристикой U_eax = сх².

Решение. Производная выходного напряжения по перемещению dU_em/dx = = 2сх. Высота каркаса h = 2kcx - b.

Для получения квадратичной функцио­нальной зависимости форма каркаса дол­жна быть треугольной с высотой h, возрас­тающей пропорционально перемещению х. Из (4.10) следует, что строгое выполнение зависимости £/_вых -f(x) из-за конечной тол­щины каркаса b может быть получено толь­ко от некоторого начального значения х* О при /_min = b/(2kc). Если же /_min считать за на­чальную точку потенциометра, то график выходной характеристики будет начинаться не с нулевого значения, как это показано на рис. 4.14.

Пример 4.3. Определить форму профиля каркаса функциональ­ного потенциометра с выходной характеристикой t/_Bblx = сух,

Решение. Производная выходного напряжения по перемеще­нию

Высота каркаса h = kc/(2jx) - b.

Из формул для h в примерах 4.2 и 4.3 следует, что при х -» 0 вы­сота каркаса потенциометра, воспроизводящего функцию f(x) = сх², стремится к нулю, а при /(х) = сух — к бесконечности.

Изготовить каркасы с нулевой или бесконечной высотой невоз­можно. Из условий прочности и технологичности рекомендуется выбирать минимальную высоту каркаса h_mln = 3-Й- мм, а максималь­ную Л_тах = 50-й50 мм.

Необходимую функциональную зависимость выходного напря­жения можно получить только не от нулевого, а от некоторого нача­льного значения перемещения х, не равного нулю при / = /_min. Сле­довательно, если принять за начальную точку потенциометра /_min, то вид зависимости и_вш =/(х) будет начинаться не с нулевого значе­ния (рис. 4,15).

Пример 4.4. Определить форму профиля каркаса функциональ­ного потенциометра с выходной характеристикой и_вш = с sin х.

Решение. Производная выходного напряжения по перемеще­нию

dt/_BbIX/dx=ccosx.

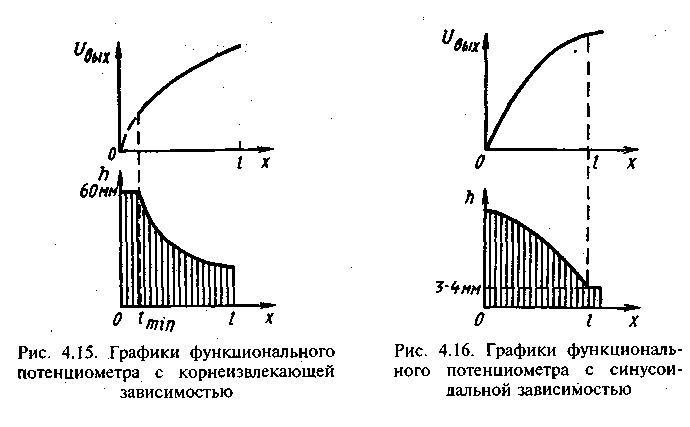
Высота каркаса h = kc cos x - b, т. е. профиль каркаса будет иметь вид косинусоиды (рис. 4.16).

Из формулы (4.10) и рассмотренных выше примеров построе­ния потенциометров с необходимым профилем видно, что высота каркаса выражается функцией, которая пропорциональна производ­ной заданной функции по перемещению.

Выполнить каркас и намотку профильного потенциометра тех­нологически довольно трудно, поэтому в большинстве случаев для получения функциональной выходной характеристики применяют ступенчатые потенциометры.

При расчете ступенчатого функционального потенциометра кривую U_Bm=f(x) заменяют отрезками прямых (т. е. аппроксими­руют). Нелинейная функция заменяется близкой к ней ломаной прямой. Количество отрезков берут таким, чтобы максимальное значение ошибки аппроксимации не превышало заданного опреде­ленного значения. При кусочно-линейной аппроксимации функци­ональный потенциометр как бы делится на несколько линейных потенциометров.

Пусть функция /(дс) задана в виде графика на рис. 4.17, а. Ап­проксимируем ее приближенной ломаной 0123. Для получения та­кой функциональной зависимости выходного напряжения от пере­мещения можно изготовить потенциометр со ступенчатым каркасом (рис. 4.17, б). Высота участков А,, А₂, А₃ выбирается таким образом, чтобы обеспечить заданные углы наклона а,, а₂, а₃ для линейных выходных характеристик на каждом из участков длиной /,, /₂, /₃.

Требуемую функциональную характеристику можно приближен­но получить, применяя каркас по­стоянной высоты h с намоткой, ко­торая на разных участках (/,, /₂, /₃.) выполняется разным шагом (рис. 4.18). Иногда на разных уча­стках намотки используют провода различных сечений или материалов с отличающимися удельными со­противлениями.

Довольно распространенным способом получения функциональ­ной зависимости между выходным напряжением и перемещением яв­ляется включение дополнительных постоянных резисторов, сопротив-

ление которых шунтирует участки намотки (рис. 4.19). На шунтиро­ванном участке наклон характеристики уменьшается, т. е. шунтиро­вание равносильно уменьшению ширины каркаса.

Контрольные вопросы

1. Как устроен потенциометрический датчик?

2. Схема включения и принцип действия потенциометрического датчика.

3. Как зависит точность потенциометрического датчика от сопротивле­ния нагрузки?

4. Что такое функциональный потенциометрический датчик?