
- •Введение
- •2 Описание работы структурной схемы
- •3.3 Вывод передаточной функции распределенного блока w2
- •3.4 Вывод передаточной функции индуктивного дифференциального
- •4 Расчет векторной энергетической системы
- •5.3.2 Прямые оценки качества сау. Передаточная функция всей системы имеет вид:
- •6.2 Прогнозирование живучести электрогидравлического преобразователя
- •8.4 Определение плановой себестоимости проведения нир
- •8.6 Оценка научной и научно – технической результативности
- •9 Безопасность жизнедеятельности
- •9.1 Охрана труда
- •9.1.1 Характеристики помещения. Лабораторные исследования и проведение экспериментов на комплексной атмосферно- вакуумной установки проводились в подвальном помещении кафедры уит, аудитории № 123.
- •9.2 Классификация и общая характеристика чрезвычайных ситуаций
- •9.3 Условия возникновения и стадии развития чрезвычайных ситуаций
- •9.4 Принципы и способы обеспечения безопасности жизнедеятельности в
- •9.3 Основные сценарии управления в чрезвычайных ситуациях
- •Список используемых источников
- •5 Беклешов в. К. Технико-экономическое обоснование дипломных проектов. – м.: Высшая школа, 1991.
- •Приложение а
3.3 Вывод передаточной функции распределенного блока w2
Входным сигналом для второго блока является выходной сигнал первого распределенного блока, то есть изменение давления Р, описываемое уравнением (6). Выходным сигналом второго распределенного блока является величина смещения поплавка относительно положения равновесия Х.
Уравнения (1), (3),(4) можно предложить для описания процессов, происходящих во втором распределенном блоке W2 ГЭПП в виде следующих уравнений:
 (26)
(26)
![]()
r 0, t 0, a 0.
 (27)
(27)
Нормирующая функция для уравнения (19) будет иметь вид:
![]() ,
(28)
,
(28)
где (t) – функция Дирака;
r – координата точки смещения поплавка ГЭПП, где определяется функция отклика;
а – кинематическая вязкость, м2/с;
Q(r,t) – величина изменения давления.
Функция Грина для (19) будет иметь вид выражения (3).
Континуальная передаточная функция для (19) в распределенных параметрах для второго блока будет иметь вид выражения (4).
Решение искомой функции запишется через функцию Грина и нормирующую функцию можно представить следующим образом:
 (29)
(29)
Для определения интегральной передаточной функции необходимо найти операторное выражение выходной величины.
Зададимся, что а = 3 м2/с.
Таким образом континуальная передаточная функция равна:
 (30)
(30)
Для дальнейших вычислений необходимо определить изображение по Лапласу нормирующей функции:
![]() ,
(31)
,
(31)
Давление потока изменяется в пределах 0 Р 5,29 Па.
Таким образом, операторное изображение выходной величины запишется:
 ,
(32)
,
(32)
Тогда интегральная передаточная функция примет вид:
 (33)
(33)
 .
(34)
.
(34)
Интегральную передаточную функцию в операторном изображении W2(r,) преобразуем в частотную, то есть произведем замену рj. В преобразованном выражении выделим действительную и мнимую части:
![]() (35)
(35)
![]() ,
(36)
,
(36)
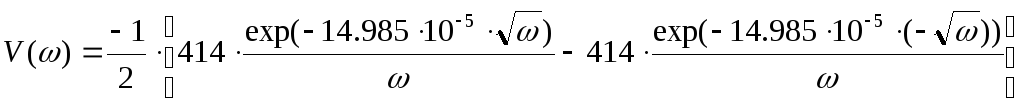 ,
(37)
,
(37)
![]() .
(38)
.
(38)
По формуле (31) строится график ЛАЧХ (рисунок 5) режима работы распределенного блока W2.

Рисунок 16 – Логарифмическая амплитудно-частотная характеристика распределенного блока W2
Передаточная функция второго блока в системе с распределенными параметрами может быть идентифицирована для дальнейшего анализа передаточной
функцией вида:
 ,
(39)
,
(39)
где k – коэффициент передачи.
Значение коэффициента k определим из графика построенной ЛАЧХ для распределенного блока W2 по формуле:
![]() (дБ),
(40)
(дБ),
(40)
k = 0,418.
При проведении аппроксимации асимптотами логарифмической функции сопрягающаяся частота имеет следующее значение:
1 = 11,7 (с-1).
Соответственно определяется постоянная времени Т1 по формуле:
 ,
(41)
,
(41)
Т1 = 0,085 (с).
Численное значение передаточной функции примет вид:
 .
(42)
.
(42)
В результате определения передаточных функций распределенных блоков W1 и W2 их можно рассматривать как блоки с сосредоточенными параметрами, что необходимо для нахождения общей передаточной функции ГЭПП.
