Математическая обработка результатов экспериментальных данных ГЭПП / Обоснов метод

4 ОБОСНОВАНИЕ МЕТОДИКИ ОБРАБОТКИ ДАННЫХ

4.1 Общие сведения

Установление закономерностей, которыми подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных – результатов наблюдений.

Первая задача математической статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.

Вторая задача математической статистики – разработать­ методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:

• оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин.

• проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого неизвестен.

Современная математическая статистика способы распределения числа необходимых испытаний до начала исследования (планирование эксперимента), в ходе исследования (последовательный анализ) и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности /8/.

Ошибки в основном происходят от несовершенства органов чувств наблюдателя, от недостатков измерительных приборов и под влиянием внешней среды. Точным или истинным значением объекта называют практически неизменный в течение определенного промежутка времени размер измеряемого объекта. А разницу между истинным значением какой-то измеряемой величины Х и измеренным значением этой величины Х_i;

ΔХ=Х-Х_i (20)

называют истинной ошибкой измерения.

Так как увеличение точности измерения сопряжено с большой затратой труда и применением дорогостоящих инструментов, а недостаточная точность измерения может привести к большим материальным убыткам, то точность измерения в конечном счете должна определяться той точностью, которая требуется для решения прак­тических задач. Требуемая точность измерений определяет выбор необходимых инструментов и методику измерения ими.

В связи с тем, что измеряемая величина и единица измерения почти всегда являются величинами несоизмеримыми, это приводит к необходимости определять некоторые доли единицы измерения, что при самом тщательном исполнении и при самых совершенных инструментах неизбежно сопровождается ошибками. Различают четыре основных типа ошибок в зависимости от принятой единицы измерения ошибки (абсолютная или относительная) и постоянства ее величины (систе­матическая или случайная)

С этой же целью повышения точности измерения рекомендуют износ одному и тому же исследователю, одним инструментом, и одинаковой температуре. Это снижает величину случайной ошибки. Случайные ошибки обязаны своим происхождением ряду причин, действие которых неодинаково в каждом опыте и не может быть практически учтено. Случайной ошибкой называют такую, величина которой различна даже для измерений, выполненных одинаковым образом. Или по-другому если среднее из ошибок равноточных измерений одной и той же величины стремится к нулю при увеличении числа измере­нии до бесконечности, то такие ошибки называются случайными.

Другой тип ошибок, величина которых одинакова во всех измерениях одним и тем же методом с помощью одних и тех же измерительных приборов, называют систематическими ошибками. Средняя величина систематической ошибки при увеличения числа равноточных измерений одной и той же величины до бесконечности стремится к некоторому пределу, отличному от нуля. Если известен закон изме­нения систематических ошибок, применяют специальную методику измерений, в процессе которых систематические ошибки будут исключаться. Такие ошибки называются исключаемыми систематическими ошибками (например, температурные).

Однако полностью исключить систематические ошибки невозможно, и поэтому измерения содержат остаточные систематические ошибки. При измерении стараются учесть и исключить систематические ошибки. Различают систематические ошибки:

- природа которых известна и величина может быть достаточно точно определена (например, температурные ошибки);

- известного происхождения, но неизвестной величина (например, погрешность измерительного прибора, в частности и, измерительной линейки);

- о существовании которых не знают, хотя величина их может быть значительной. Например, при определении плотности металла по образцу, внутри которого оказался пузырек воздуха, ошибка может быть большой. Одним из наиболее надежных способов убедиться в отсутствии таких погрешностей - проведение измерения интере­сующей величины другим методом и в других условиях;

-обусловленные свойствами измеряемого объекта.

Ошибки при эксперименте являются суммой элементарных ошибок различного происхождения. В зависимости от источника появления ошибки (объект измерения, наблюдатель, инструменты и внешняя среда) и типа ошибок (грубые, и неизбежные, систематические или случайные) можно дать схему классификации ошибок результатов эксперимента.

Систематическая ошибка по величи­не постоянна при каждом опыте ,не зависит от числа опытов. А так как величина случайной ошибки различна при каждом опыте, то точность результата эксперимента повышается с увеличением числа экспериментов. Этот вывод можно сформулировать в виде двух правил.

– Если определяющей является систематическая ошибка, то ее величина существенно больше величины случайной ошибки то присущей данному методу, то достаточно выполнять измерение, опыт один раз.

– Если определяющей является случайная ошибка, то опыт , измерения следует производить несколько раз. Число измерений выбирают таким, чтобы среднее арифметическое случайной ошибки» было бы меньше систематической ошибки. Окончательную ошибку результата опыта будет снова определять систематическая ошибка. Таким образом, необходимое число измерений определяется в конечном итоге соотношением величины и систематической и случайной ошибок. С точки зрения повышения точности измерения, необходимо добиваться, чтобы систематические ошибки были больше случайных.

Это позволит снизить число измерений (а следовательно, и экспериментов), в принципе свести к одному. Этой цели и должна быть подчинена методика исследования, в которую входит не только методика проведения исследования, но и методика измерения.

С увеличением числа измерений среднее значение случайной ошибки сходится по вероятности к математическому ожиданию, которое свободно от случайности. С увеличением числа измерений величина случайной ошибки приближается к систематической, никогда не будет меньше. Здесь опять справедливо правило: нельзя сделать ошибку меньшей, чем та, которая определяется погрешностью измерительного устройства.

Для этого следует знать свойства случайных ошибок, установить закономерности возникновения и накопления ошибок, уметь производить оценку точности и наметить пути увеличения точности при разработке методики исследования.

Таким образом под ошибками измерения нужно иметь в виду ошибки эксперимента. Для снижения величины ошибок результатов исследования необходимо прежде всего снизить величину случайной ошибки результатов эксперимента:

– из-за непостоянства внешних условий.(под постоянством внешних условий имеется в виду не абсолютное постоянство, а одинаковость условий для эталона и экспереминтального объекта);

– из-за непостоянства остальных факторов: состояния объекта исследования, наблюдателя, инструмента. ; В какой мере внешние условия могут оказать влияние на ошиб­ку результата исследования, можно судить по анализу влияния раз­личных факторов на интенсивность изнашивания деталей.

Число опытов, экспериментов зависит от соотношения требуемой с практической точки зрения точности результатов и точности, получаемой при единичном эксперименте.

При измерениях, когда основную роль играют случайные ошибки, все оценки точности измерения можно сделать только с некоторой вероятностью. Случайные ошибки имеют нормаль­ный закон распределения, математическое ожидание которого равно нулю. Теория вероятностей дает возможность подсчитать вероятность любой величины ошибки. Если каждое измерение дает несколько отличные от других измерений результаты, то случайная ошибка играет существенную роль. За наиболее вероятное значение измеряе­мой величины (при нормальном законе распределения ошибок) следует принять ее среднее арифметическое значение

, (21)

где Х1 , -Х2... , Хn- результаты отдельных измерений.

Суждение о точности выполненных измерений можно получить по величине колебаний результатов измерений: чем больше разбросаны результаты измерений в ряду, чем сильнее они отличаются друг от друга, тем менее точны измерения. Для оценки величины случайной ошибки измерения существует несколько способов. Иногда применяют среднюю арифметическую ошибку. Наиболее распространена оценка с помощью стандартной или средней квадратической ошибки (ее часто называют стандартом измерений). Средняя квадратическая ошибка характеризует условия измерений. Средней квадратической ошибкой называется

. (22)

Когда n стремится к бесконечности , то подверженная случайным колебаниям величина стремится к некоторому постоянному значению б , которое можно назвать статистическим пределом ,

б=limб*. (23)

Собственно говоря, именно этот предел и называется средней квадратической ошибкой. Квадрат этой величины называется дисперсией. В действительности, однако, всегда вычисляют не величину б, а ее приближенное значенье б*, которое тем ближе к б, чем больше n.

Так как никогда не бывает бесконечного ряда наблюдений, стандарт (среднее квадратаческое отклонение) б остается неизвестным, приходится пользоваться его приближенным значением б*, которое в свою очередь, определяется со средней квадратичеокой ошибкой вычисленной по приближенной формуле:

(24)

или в относительном выражении

. (25)

4.2 Статистический анализ данных

Предварительные данные о соответетвии экспериментальных данных принятой гипотезе получают по результатам их статистической обработки. С помощью критерия Пирсона проверяют правомерность принятой формы распределения, коэффициента корреляции - линейной зависимости и т. д.

4.2.1 П р о в е р к а з н а ч и м о с т и с п о м о щ ь ю λ² критерия. С помощью статистического критерия λ² проверяют справедливость выдвинутой гипотезы (соответствия распределения экспериментальных данных принятому аналитическому, например, нормальному две группы экспериментальных данных, полученных в разных условиях имеют одинаковую функцию распределения, принадлежат к одной совокупности).

Например, с помощью λ², так называемого критерия Пирсона можно проверить согласованность статистического распределения полученного по экспериментальным данным, и аналитического, после определения расчетом параметров распределения. Распределение λ², мера расхождения между аналитическим и статистическим распределениями, по Пирсону практически не зависят от функции распределения и от числа опытов n, а зависит только от числа разрядов К. Для удобства вычислений, чтобы иметь дело с целыми числами, λ² определяют по формуле

(26)

где n_i - число значений в i-м разряде;

p_i - аналитическая вероятность в i-м разряде;

- общее число независимых опытов, экспериментов.

Распределение λ² зависит от параметров f, от числа “степеней свободы” распределения, от числа независимых групп наблюдений. Число "степеней свободы" f равно числу разрядов К, минус число независимых условий ("связей"), наложенных на частость р распределения экспериментальных данных. Так, во всех случаях накладывается требование

. (27)

Если же аналитическое распределение подбирают с таким условием чтобы совпадали аналитические и статистические средние значения, то должно быть

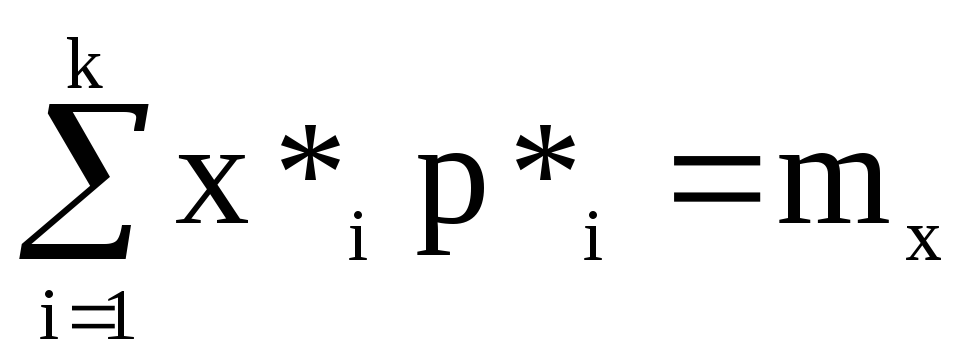. (28)

Если же требуется, чтобы совпали аналитическая и статистическая дисперсии, то должно быть

. (29)

Так что, если число наложенных связей S (в данном случае перечислено три вида связи), то число степеней свободы

f=K-S. (30)

При определении параметров нормального распределения исходят из условия, чтобы

m_x= m_x*, D_x = D_x*. (31)

Для распределения λ² составлены специальные таблицы, по которым для каждого значения λ² и числа степеней свободы f можно найти вероятность р расхождения за счет чисто случайных причин.

При большой р вероятность расхождения между статистическим и аналитическими распределениями случайные, вероятность которых р. Если же вероятность р очень малая, то это означает, что вероятность случайности в расхождении между статистическим и аналитическим распределениями очень мала, они органически несов­местимы; эти расхождения не случайны. При малой вероятности р гипотезу отвергают, как неправдоподобную; а если вероятность р относительно большая, то гипотезу можно признать не противореча­щей опытным данным. Следует обратить внимание на слова, что гипотеза не противоречит опытным данным. Это вовсе не означает, что гипотеза справедлива. Нельзя дать рецепта и по величине веро­ятности р, при которой гипотезу можно решительно отвергнуть.

При использовании критерием λ² число наблюдений n_i в отдельных разрядах рекомендуется иметь не менее 5. При меньшей величине n_i лучше объединить разряды.

С помощью критерия λ² можно проверить принадлежность к одной совокупности двух и более групп событий.

Нужно отметить что статистический анализ даёт лишь общие или частично сформулировавшиеся представления, является начальной стадией анализа, после которой выдвинутую гипотезу проверяют тщательно или отвергают.

4.2.2 П о р я д о к с т а т и с т и ч е с к о й о б р а б о т к и р е з у л ь т а –

т о в э к с п е р и м е н т а . Определим среднеарифметическое значение для каждого значения случайной величины по формуле /10/.

, (32)

где X_i – значения случайных величин. Это значение представляет собой оценку истинного значения.

Применительно к нашим данным формула 13 примет вид:

, (33)

где I_1-7 – значения случайных величин силы тока.

Вычислим отклонения результатов измерений от среднего значения по формулам:

_i=X–X_i; (34)

₁=I–I₁; ₂=I–I₂; ₃=I–I₃; ₄=I–I₄; ₅=I–I₅; ₆=I–I₆; ₇=I–I₇. (35)

Определим оценку значения средней квадратичной погрешности измерения по формуле:

. (36)

Определим среднеквадратическое отклонение среднеарифметического значения Х по формуле:

. (37)

Вычислим доверительный интервал, соответствующий доверительной вероятности Р_g=0,95 и числу измерений n: – значение квантиля определяется по таблице [ ], где это значение равно 2,45.

Определим нижнюю границу доверительного интервала по формуле

; (38)

. (39)

Определим верхнюю границу доверительного интервала по формуле

; (40)

. (41)

Определим нижнюю и верхнюю границы погрешностей измерения по формуле:

. (42) . (43)

Рассчитаем значения коэффициента корреляции для случайных величин

. (44)

Применительно к нашим данным формула 25 примет вид:

. (45)

Выбрав для I и t только средние значения формула 26 примет вид

. (46)

В результате обработки экспериментальных данных статистическим методом изучим закономерности массовых случайных явлений, сможем спрогнозировать их характеристики и повлиять на ход этих явлений, а также контролировать их и ограничивать область действия случайности.