шпоргалка / электроника / решение задач по электронике

РЕШЕНИЕ ЗАДАЧ ПО ЭЛЕКТРОНИКЕ

1. Имеется сплавной германиевый p-n-переход с N_д = 10³N_а , причем на каждые 10⁸ атомов германия приходится один атом акцепторной примеси. Определить контактную разность потенциалов при температуре Т=300 К (плотности атомов N и ионизованных атомов n_i принять равными 4,4*10²²см^-3 и 2,5*10¹³ см ^-3 соответственно).

Решение. Определим концентрацию акцепторных атомов:

(N=4,4*10²² см^-3 — плотность атомов германия).

Концентрация атомов доноров N_Д=10³ N_a=4,4*10¹⁷cм^-3.

Контактная разность потенциалов

2. Имеется кремниевый p-n-переход с N_д = 10³N_а , причем на каждые 10⁸ атомов кремния приходится один атом акцепторной примеси. Определить контактную разность потенциалов при температуре Т=300 К (плотности атомов N и ионизованных атомов n_i принять равными 5*10²²см^-3 и 10¹⁰ см ^-3 соответственно).

Решение. Определим концентрацию акцепторных атомов:

(N=5*10²² см^-3 — плотность атомов кремния).

Концентрация атомов доноров N_Д=10³ N_a=5*10¹⁷cм^-3.

Контактная разность потенциалов

3. Удельное сопротивление р-области германиевого p-n-перехода ρ_р=2 Ом*см, а удельное сопротивление n-области ρ_n =1 Ом*см. Вычислить контактную разность потенциалов (высоту потенциального барьера) при Т = 300 К. n_i = 2,5*10¹³ см ^-3.

Решение. Известно, что удельное сопротивление р-области полупроводника , где N_a — концентрация акцепторов; е — заряд электрона; µ_р — подвижность дырок. Отсюда

Аналогично найдем концентрацию доноров в n-области полупроводника:

Контактная разность потенциалов

4. В германиевом p-n-переходе удельная проводимость р-области σ_р=10⁴ См/м и удельная проводимость n-области σ_n=10² См/м. Подвижности электронов μ_п и дырок μ_p в германии соответственно равны 0,39 и 0,19 м²/(В*с). Концентрация собственных носителей в германии при Т=300К n_i=2,5*10¹⁹ м^-3. Вычислить контактную разность потенциалов (высоту потенциального барьера) при Т=300 К.

Решение. Для материала р-типа σ_P≈р_Peµ_p, где σ_р — удельная проводимость; µ_p — подвижность дырок; р_р—концентрация дырок; е — заряд электрона. Отсюда

Аналогично для материала n-типа

Концентрация

Контактная разность потенциалов

5. Прямой ток эмиттера транзистора п-р-п составляет I_Э=2 мА, коллекторная цепь разорвана. Определить: а)напряжение на эмиттерном и коллекторном переходах; б)напряжение эмиттер—коллектор, полагая I_КБ0 = 2 мкА, I_ЭБ0=1,6 мкА, α = 0,98. В каком режиме работает транзистор?

Решение.

Откуда

Напряжение база—коллектор

Следовательно, транзистор работает в режиме насыщения.

б) Напряжение эмиттер — коллектор

6. Транзистор, имеющий α = 0,995, α_I = 0,1, I_ЭБК = 10^-14 А, I_КБК = 10^-13 А, включен в схему. Определить напряжение коллектор—эмиттер U_КЭ, ток I_К..

Решение. Напряжение коллектор — эмиттер найдем из выражения

Откуда

Ток коллектора

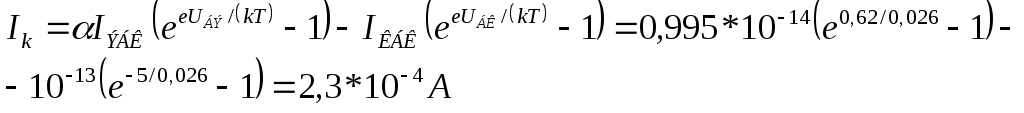
7. Дана схема, изображенная на рис. Известно, что транзистор работает в активном режиме. Предполагая, что сопротивление резистора R_Э достаточно велико по сравнению с сопротивлением эмиттерного перехода и что сопротивление коллекторного перехода r_K »R_H, найти коэффициент усиления по напряжению к_U. Пренебречь обратным током коллектора I_КБ0.

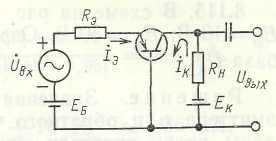
Решение. Выходное напряжение

Пренебрегая падением напряжения на эмиттерном переходе, можно написать:

Пренебрегая обратным током коллектора I_КБ0, найдем ток коллектора

Следовательно,

Коэффициент усиления по напряжению

8. В схеме на рис. R_Э = 2 кОм, E_Э = 2 B, R_б =15 кОм, E_Б = 3B, R_Н = 4 кОм, E_к=16 В. Транзистор имеет α = 0,98; I_КБ0 = 10 мкА. Определить ток коллектора.

Решение. Используя второй закон Кирхгофа для входной цепи (эмиттер — база), запишем: . Но ток базы

следовательно, .

Откуда

Ток коллектора:

9. В усилителе на рис. при ток стока . Определить: а) сопротивление резистора R_И, если падением напряжения I_ЭR_Э пренебречь; б) Е_с, если R_Н =10 кОм, U_CИ = 4 В.

Решение.

10. В усилительном каскаде с общим истоком сопротивление нагрузки R_Н = 20 кОм. Эффективное входное сопротивление полевого транзистора 20 кОм, рабочая крутизна S=2 мА/В. Определить коэффициент усиления каскада.

Решение. Результирующее сопротивление нагрузки

Коэффициент усиления каскада