Косвенные оценки качества

При гармонических воздействиях качество системы оценивают по АФХ, АЧХ, ФЧХ и ЛАЧХ. Для оценки качества переходного процесса используются:

Показатель колебательности М – это отношение максимального значения АЧХ замкнутой системы к ее значению при w=0. М=A_max(w)/A(0), при А(0)=1 показатель колебательности М= A_max(w).

Резонансная частота w_p, при которой АЧХ замкнутой САУ имеет максимум. При ней колебания проходят через систему с наибольшим усилением.

Полоса пропускания системы – интервал частот от w=0 до w₀, при котором выполняется условие A(w₀)<=0.707A(0).

Частота среза w_ср, при которой АЧХ принимает значение, равное 1.

8. Критерий устойчивости Михайлова, кривая Михайлова.

Данный метод используется для исследования устойчивости замкнутой системы.

Является геометрической интерпретацией принципа аргумента.

Пусть дано характеристическое уравнение системы

Необходимо привести характеристический полином к комплексной форме D(jw)=X(w)+jY(w)=D(w)e^j(w). Функции D(w) и (w) представляют собой модуль и фазу (аргумент) вектора D(jw). При изменении частоты w он будет описывать некоторую кривую, называемую кривой (годографом) Михайлова.

Для того, чтобы система была устойчивой необходимо, чтобы все корни характеристического уравнения принадлежали левой полуплоскости, тогда ArgD(jw)=n/2 при 0<w<

Для того чтобы САУ была устойчива, необходимо и достаточно, чтобы кривая (годограф) Михайлова при изменении частоты w от 0 до , начинаясь при w=0 на вещественной положительной полуоси, обходила против часовой стрелки последовательно n квадрантов координатной плоскости, где n – порядок характеристического уравнения.

Эта кривая для устойчивых систем имеет спиралевидную форму, причем конец ее уходит в бесконечность в том квадранте координатной плоскости, номер которого равен степени характеристического уравнения.

9. Типовые нелинейные звенья систем управления, их графические характеристики.

Нелинейные звенья САУ описываются нелинейными уравнениями. Нелинейные звенья и системы классифицируются по физическим принципам действий, по способам аппроксимации, по статическим и динамическим характеристикам. Чаще всего используют нелинейные звенья:

1. С гладкой нелинейной характеристикой.

2. С кусочно-линейной характеристикой.

3. Характеристики, описываемые уравнениями, которые содержат произведения переменных или их производные.

4. Логические нелинейные звенья.

Различают статические и динамические нелинейные системы. Статические представляют в виде нелинейных статических характеристик. Они могут быть однозначными, неоднозначными релейными, неоднозначными и неоднозначными в виде поля.

Динамические нелинейности представляются в виде нелинейных диф.уравнений с переменными коэффициентами при производных. Все нелинейные звенья делят на аналитические и неаналитические. Все нелинейности делятся на сопутствующие и преднамеренные. В зависимости от этого все нелинейные САУ делятся на группы:

1. С сопутствующими нелинейностями, то есть нелинейности, спроектированные как линеаризованные, но из-за насыщения люфта, мертвого хода, сухого трения являющиеся практически нелинейными.

2. С преднамеренными нелинейностями – системы, проектированные как нелинейные.

10. Фазовый портрет нелинейной системы управления. Анализ поведения системы по фазовому портрету.

Н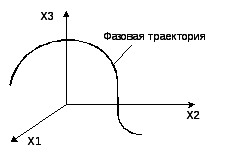елинейные системы описываются нелинейными дифференциальными уравнениями, общих методов решения которых нет. В случае отсутствия решения анализ систем выполняется методом фазового пространства. Фаза или состояние системы характеризуется рядом параметров: X – вход, U – выход, - скорость изменения входного сигнала,  - точность управления. Чем выше порядок системы, тем больше параметров, описывающих состояние системы. Для системы n-го порядка параметров будет n. В этом случае система описывается n-мерным пространством с одноименным названием координат. Такое пространство называется фазовым. Траектория получается при перемещении точки, характеризующей состояние системы. Наибольшей информативностью обладает фазовая траектория в пространстве отклонений. Для каждой координаты Х переходит к ее приращениям относительно установившегося значения. . В качестве другой координаты обычно используется скорость изменения приращения. Фазовая траектория построения на осях X и есть фазовый портрет. Пусть некоторая система выведена из состояния устойчивости. В точке М₀. Состояние системы изменится в соответствии с линией 1. Эта линия в процессе работы системы приближается к началу координат, что соответствует устойчивой системе. Если систему вывести в точку М₁, то состояние системы описывается фазовой траекторией 2, которая удаляется от начала координат, что соответствует неустойчивой системе. Фазовый портрет строится следующими способами: метод изоклин, метод припасовывания.

По данным фазового портрета можно косвенным образом оценить качество переходного процесса.