1. Понятие соединения систем и их элементов. Струк­турные схемы.

Каждая сложная система состоит из ряда более простых сис­тем, взаимодействующих между собой определенным образом. В зависимости от характера взаимодействия этих систем они могут быть связаны между собой различными способами. Ос­новными типами соединений систем в сложных системах явля­ются последовательное соединение, параллельное соединение и обратная связь.

Последовательным соединением систем называется такое со­единение, когда выход каждой системы связывается с входом следующей системы, т. е. когда выходная переменная каждой системы служит входной переменной для следующей системы. Последовательное соединение стационарных линейных систем дает стационарную линейную систему, передаточная функция которой Ф(s) равна произведению передаточных функций со­единяемых систем: Ф(s)= Ф₁(s) Ф₂(s)

Параллельным соединением систем называется такое соеди­нение, при котором входная переменная подается одновременно на несколько систем, а их выходные переменные суммируются. передаточная функция параллельного соединения стационар­ных линейных систем равна сумме передаточных функций со­единяемых систем: Ф(s)= Ф₁(s)+ Ф₂(s).

Рассмотрим систему, состоящую из стационарной линейной системы с передаточной функцией Ф₁(s), замкнутой отрица­тельной обратной связью, содержащей стационарную линейную систему с передаточной функцией Ф₂(s). Для определения пере­даточной функции Ф(s) этой системы рассмотрим обратную систему, которая по доказанному имеет передаточную функцию 1/Ф(s). Обратная система представляет собой параллельное со­единение системы с передаточной функцией 1/Ф₁(s) и системы с передаточной функцией Ф₂(s)

Отсюда находим передаточную функцию интересующей нас

системы с обратной связью:

Очевидно, что при любых видах соединений линейных сис­тем система, полученная в результате соединения, будет линей­ной.

2. Критерий устойчивости рауса — гурвица.

Критерий Рауса

Критерий устойчивости Рауса заключается в том, что все клетки таблицы заполняются коэффициентами характеристического уравнения. В первой строке располагаются все коэффициенты с четными индексами: а₀, а₂, а₄…; во второй строке все коэффициенты с нечетными индексами: а₁, а₂, а₃… Любой элемент таблицы записывается с индексом № столбца k и № строки i, т.е. С_ik. Элементы остальных клеток таблицы начиная с третьей строки составляются на основе следующего выражения:

С_ik=C _{(i -2) ,(k+1)} –C_{(i-1), (k+1)}

Для того, чтобы система была устойчива необходимо и достаточно, чтобы все коэффициенты первого столбца были положительны.

Критерий Гурвица

Это алгебраический критерий, по которому условия устойчивости сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы.

Возьмем характеристический полином, определяющий левую часть уравнения системы, где полагаем а₀>0, что всегда можно обеспечить умножением при необходимости полинома на -1.

Составим из коэффициентов этого полинома определитель.

Этот определитель называется определителем Гурвица. Он имеет п строк и п столбцов. Первая строка содержит все нечет­ные коэффициенты до последнего, после чего строка заполняет­ся до положенного числа п элементов нулями. Вторая строка включает все четные коэффициенты и тоже заканчивается ну­лями. Третья строка получается из первой, а четвертая — из второй сдвигом вправо на один элемент. На освободившееся при этом слева место ставится нуль. В результате в главной диа­гонали определителя оказываются последовательно все коэф­фициенты, кроме a₀..

Условие устойчивости заключается в требовании положи­тельности определителя Гурвица и всех его диагональных ми­норов.

Д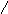ля , и условия устойчивости сводятся к не­равенствам: а₀>0; а1>0.Отсюда, например, звено первого поряд­ка с передаточной функцией является k/(Tp+1)устойчивым, а звено с передаточной функцией k/(Tp -1)- неустойчивым.