5. Построение логарифмической характеристики корректирующего устройства по лачх исходной системы и желаемой лачх

Если в САР имеется последовательное корректирующее устройство, то ее желаемую передаточную функцию можно представить в следующем виде:

W_ж(s)=W_к(s)W_н(s), откуда при s = jω имеем логарифмические амплитудную H_к(ω)= H_ж(ω)-H_н(ω) и фазовую θ_к(ω)= θ_ж(ω)-θ_н(ω) частотные характеристики. Подняв неизменяемую логарифмическую амплитудную характеристику до уровня желаемой и построив фазовую частотную характеристику θ_ж(ω), определим запасы устойчивости системы по фазе и модулю. Если они соответствуют требованиям технических условий, то, получим логарифмическую амплитудную характеристику последовательного корректирующего устройства.

Рассмотрим синтез САР с параллельным корректирующим устройством. Запишем передаточную функцию системы в виде

При условии, что |W_н(jω)W_к(jω)| » 1 имеем | W_к |=1/| W_ж |, или Н_к(ω)= -Н_ж(ω), где Н_ж(ω) —желаемая логарифмическая амплитудная характеристика синтезируемой системы.

Для обеспечения требуемого порядка астатизма проектируемой системы необходимо, чтобы порядок нуля передаточной функции W_к(s) был не ниже порядка полюса W_н(s) при S = 0.

6. Показатели качества управления, их определение по переходным и ач характеристикам системы.

Прямые показатели:

Время переходного процесса - время регулирования системы; определяется как интервал времени от момента приложения какого-либо воздействия до времени вхождения в пятипроцентную трубку ().

Перерегулирование или (максимальная динамическая ошибка) – определяется выражением .

Колебательность n – число колебаний системы от момента воздействия на нее до перехода в установившееся состояние.

Время нарастания регулируемой величины – время, при котором выходная величина достигает своего максимального значения.

Время первого согласования - время, за которое регулируемая величина первый раз достигает своего установившегося значения.

Качество переходных процессов численно характеризуется следующими показателями качества.

Косвенные показатели

Показатель колебательности определяется выражением .

Резонансная частота - частота, при которой АЧХ достигает максимального значения .

Частота среза - частота, при которой значение АЧХ равно единице. Характеризует длительность переходного процесса (чем меньше , тем хуже быстродействие системы, то есть больше время регулирования системы).

Полоса пропускания – время наилучшего прохождения сигнала по системе. Для ее определения вычисляется величина ,

В первом приближении дли­тельность переходной характе­ристики может быть оценена по величине резонансной частоты _p .Так как частота колебаний переходной характеристики примерно равна _p, время t_max1 дос­тижения первого максимума переходной характеристикой близко

половине периода колебании этой частоты t_max1=/_p.

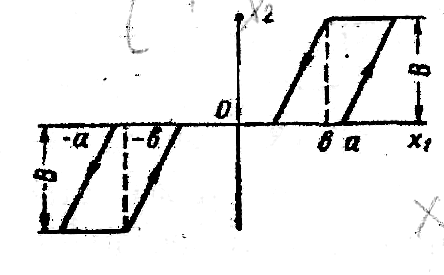
7. Типовые нелинейные звенья систем управления, их графические характеристики.

Нелинейные системы по способу аппроксимации

- с гладкой нелинейной характеристикой

- с кусочно-линейной характеристикой

- логические нелинейные элементы

Нелинейные статические характеристики

1. однозначная нелинейная характеристика

2. неоднородная гистерезисного типа

3. релейная гистерезисного типа

4. неоднородная в виде поля (свет-фотодиоды)

Зоны нечувствительности характеристик различных элементов систем регулирования можно объяснить различными причинами, зависящими от конструктивного выполнения данного устройства, типа его и т. д. Схема управления электродвигателем при помо­щи реле. Нелинейная характеристика с зоной нечувствительности. При отклонении контакта больше чем на а (т.е., если |x| >а) на зажимы двигателя подается постоянное напряжение х₂=u. Характеристика схемы которая может быть записана

Нелинейная характеристика элемента ограниченной мощности при наличии зоны нечувствительности. Уравнение этой характеристики может быть записано в виде:

Нелинейная характеристика гистерёзисного типа. Эта характе­ристика отличается от предыдущей наличием гистерезисной петли. При изменении x₁ от нуля до а выходная величина остается равной нулю. При х₁ > а х₂= к(х1 — а). При уменьшении x₁ до значения b х₂ остается постоянным и равным b. При х₁<а — bх₂= к(х1 — b)