16 Математическая модель сау
Большинство ЛСА можно привести к двум структурам, упрощенная схема которых:
а
)
б)
Рисунок 33
На этих схемах управляющий сигнал 2 формируется в задающем устройстве З. Он сравнивается в устройстве 3 с выходными сигналами, который измеряется датчиком Д параллельно. В результате сравнения сигналов образуется сигнал разности 4, поступающий через устройство управления 5 и 6 на объект регулирования ОУ. От действия сигнала возмущения 8, поступающего в систему через сумматор 9, происходит некоторое искажение выходного сигнала 10. Замыкание системы осуществляется с помощью главной ОС 12. Если в этих рисунках исключить задатчик, то получим систему автоматической стабилизации, обрабатывающий сигнал возмущения.
Рисунок 33 б) от а) отличается тем, что в нем для получения более высокой точности, применяются три датчика параллельно. Которые не только измеряют выходной сигнал 10, но и сигнал управления 2 и возмущения 8. Эти два сигнала после прохождения устройства 5, поступают на сумматор 13 и уменьшают влияние синтеза и анализа на ошибку ЛСА. Практически все ЛСА при решении задач синтеза и анализа сводится к этим двум схемам. При этом пользуются правилами преобразования структурных схем, выделяют линейную, нелинейную и цифровую части.
17 Математические модели нелинейных объектов лсу
Существенные нелин. Элементы – это те элементы, которые нельзя аппроксимировать касательной с малой погрешностью в некоторой окрестности близкой к рабочей точке. К ним относятся: ступенчатые, кусочно-линейные и многозначные функции с точками разрыва первого рода, а также степенные и транстендентые функции.
Для математического описания таких нелинейностей применяют эквивалентные передаточные функции, зависящие от коэффициентов линеаризации, которые получают путем минимизации среднего квадрата ошибки воспроизведения заданного входного сигнала. Форма входных сигналов, поступающих на вход нелинейностей, может быть произвольна. На практике наибольшее распространение получили гармонические и случайные виды входных сигналов и их временные комбинации. Соответственно и методы линеаризации называются гармоническими и статическими.
Весь класс существенных нелинейностей
разделен на две группы. К 1ой группе
относятся однозначные нелинейности, у
которых связь между входными
и выходными
сигналами, зависит только от формы
статической характеристики нелинейности
.
.
В этом случае, при определенной форме
входных сигналов:
,
с помощью матрицы линеаризации
можно найти приближенное значение
выходных сигналов:
.
В этом случае эквивалентная передаточная
функция равна коэффициентов линеаризации:
.
(V)
Ко второй группе относят двузначные
(многозначные) нелинейности, у которых
связь между входными и выходными
сигналами зависит не только от формы
статической характеристики, но так же
определяется предысторией входного
сигнала.
.
Для учета влияния предыстории входного
сигнала будем учитывать не только сам
сигнал
,
но и скорость его изменения, дифференциал
.
При входных сигналах:
приближенное значение входного сигнала
будет:
,
(W)
где
и
- матрицы коэф. гармонической линеаризации
двухзначных нелинейностей;
- период колебания по правой гармонике;
- гармоническая функция.
Эквивалентная передаточная функция:
.
Существуют нелинейности более общего вида:
,
,
где
и
- коэффициенты гармонической линеаризации;
- номер гармоники.
.
(N)
Пользуясь (V), (W) и (N) определим обобщенную формулу для вычисления передаточной функции однозначных и двухзначных нелинейностей.
В случае однозначной нелинейности
матрица коэффициентов линеаризации
,
зависящая от параметров вектора
,
выбирается, таким образом, чтобы
линеаризовать среднее значение квадрата
разности между точным
и приближенным
сигналами на входе:
,
где «черта сверху» - это силовое усреднение.
.
После преобразований, упрощений,
ухищрений и усыпления бдительности,
получим эквивалентную передаточную
функцию в виде системы матриц:
,
.
,
.
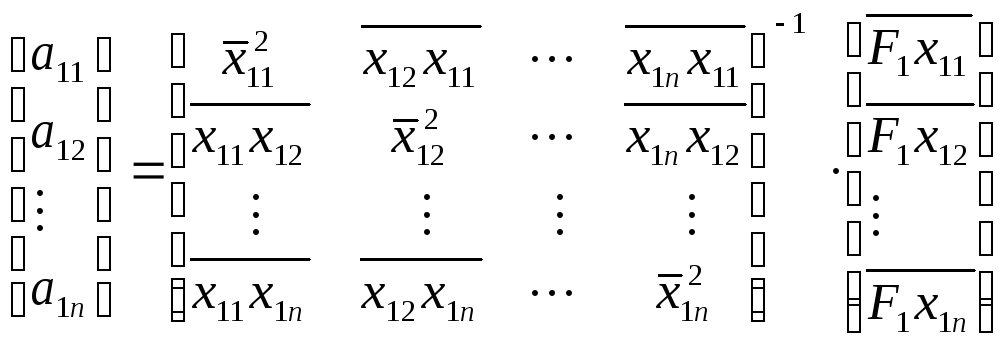Существует два типа двухзначных нелинейностей: пассивные и активные.
Под пассивными – понимаются такие двузначные нелинейности, которые за один период входного сигнала нелинейной характеристики обходится против часовой стрелки. В этом случае в выходном сигнале наблюдается фазовое запаздывание. Если обход нелинейной характеристики проходит по часовой стрелке, то двузначная нелинейность является активной и в выходном сигнале имеет место фазовое опережение. Активные нелинейности применяют в устройствах коррекции СА для обеспечения устойчивости. Реализация таких устройств может быть выполнена на электронных элементах или в виде рабочей программы.