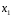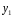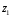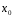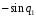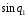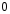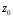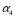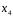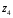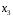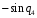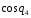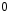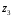Расчет промышленного манипулятора

7

Задание

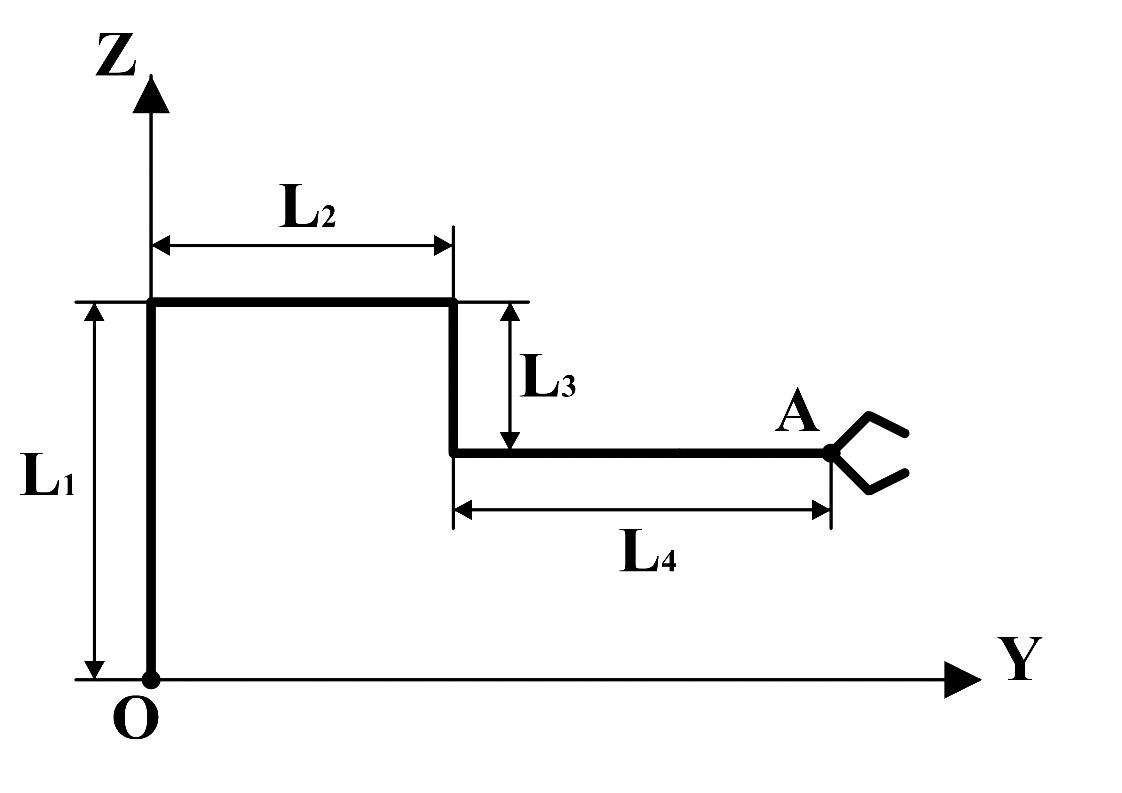
Разработать векторно-матричную модель кинематики четырехзвенного манипулятора (положение точки А в подвижной системе координат относительно неподвижной системы координат) по имеющемуся рисунку (см. рисунок 1).

Рисунок 1 (исходная схема)

Расположим 1СК так чтобы она совпадала с неподвижной или нулевой системой координат 0СК. Направим ось Z1 вдоль оси вращения 1-ого звена, ось Y1 сонаправлена с направлением звена 1, а ось X1 дополняет систему 1СК до правосторонней системы координат.

Расположим 2СК на сочленении 2 и 3 звеньев. Ось Z2 параллельна оси Z1, ось Y2 параллельна Y1, а ось X2 дополняет систему до правосторонней системы координат.

Расположим 3СК на сочленении звеньев 3 и 4.Ось Z3 параллельна оси Z2, ось Y3 параллельна Y4, а ось X3 дополняет систему до правосторонней системы координат.

Ось 4СК также расположим на сочленении звеньев 3 и 4.Ось Z4 направлена вдоль оси вращения 4-ого звена, ось Y4 направлена вдоль оси 4-ого звена, а ось X4 дополняет систему координат до правосторонней системы координат.

Расположение систем координат показано на рисунке 2

Рисунок 2 (расчетная модель манипулятора)

Конфигурация механизма и положение рабочего органа определяется четырьмя обобщенными координатами: двумя линейными (q2 и q3) и двумя угловыми (q1 и q4)

Составим матрицу направляющих косинусов позволяющую определить направление осей 1СК по отношению к осям неподвижной системы координат 0СК.Система 1СК повернута относительно системы 0СК на угол q1 вокруг оси Z

Составим переходную матрицу которая позволит определить положение 1СК по отношению 0СК.Для этого в структуру матрицы направляющих косинусов добавим координаты вектора, определяющего положение начала 1СК относительно 0СК

Положение 1СК совпадает с 0СК

Составим матрицу направляющих косинусов позволяющую определить направление осей 2СК по отношению к осям неподвижной системы координат 1СК.

Составим переходную матрицу которая позволит определить положение 2СК по отношению 1СК.Для этого в структуру матрицы направляющих косинусов добавим координаты вектора, определяющего положение начала 2СК относительно 1СК

2СК смещена относительно 1СК по оси Z на (L1+q2) и по оси Y на L2

Составим матрицу направляющих косинусов позволяющую определить направление осей 3СК по отношению к осям неподвижной системы координат 2СК.

Составим переходную матрицу которая позволит определить положение 3СК по отношению 2СК.Для этого в структуру матрицы направляющих косинусов добавим координаты вектора, определяющего положение начала 3СК относительно 2СК

3СК смещена относительно 2СК по оси Z на (-L3) и по оси Y на q3

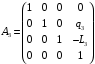
Составим матрицу направляющих косинусов позволяющую определить направление осей 4СК по отношению к осям неподвижной системы координат 3СК.

4СК смещена относительно 3СК по оси Z на (q4)

Составим переходную матрицу которая позволит определить положение 4СК по отношению 3СК.Для этого в структуру матрицы направляющих косинусов добавим координаты вектора, определяющего положение начала 4СК относительно 3СК

Положение 4СК совпадает с 3СК

Перемножаем переходную матрицу А1 и переходную матрицу А2 для получения матрицы В2

Далее перемножаем переходную матрицу А3 с матрицей В2 для получения матрицы В3

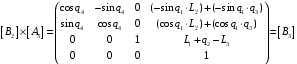
Далее перемножаем переходную матрицу А4 с матрицей В3 для получения матрицы В4

Для получения матрицы Нужно перемножить матрицу В4 и однородные координаты

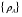
Необходимо выполнить проверку. Задаем обобщенным координатам следующие значения:

Подставим значения обобщенных координат в систему уравнений 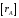, получаем;

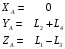
Схема манипулятора в режиме проверки

Вывод: расчетное значение совпадают с графическими - это значит что расчет произведен верно.