Добавил:

LuPuS Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Теоретические основы электротехники

Файл:

шпоры тоэ нов (1)

.pdf

Скачиваний:

Добавлен:

12.01.2019

Размер:

1.25 Mб

Скачать

☆

Б1. Электрическая цепь – совокупность

Б5. Двухполюсник, не содержащий внутри

устройств,

образующих

пути

для

себя

источников

энергии

называется

электрического

тока,

электромагнитные

пассивным.

Последовательное

процессы в которой могут быть описаны с

соединение — соединение, при котором

помощью

понятий

об

электродвижущей

конечный вывод (полюс, зажим) одного

силе,

токе

напряжении.

элемента

соединяется

начальным

Электромагнитные

процессы,

выводом (полюсом, зажимом) другого

протекающие

устройствах

элемента так, чтобы ток во всех

электрической цепи, могут быть описаны

элементах соединения

был одинаков.

при помощи понятий об электродвижущей

Параллельное соединение — соединение

силе (Э.Д.С.), токе и напряжении.

при котором начальные выводы (полюсы,

Электрические цепи, в которых получение

зажимы) элементов соединяются в один

электрической энергии, её передача и

узел и конечные выводы (полюсы,

преобразование

происходят

при

зажимы) элементов соединяются в другой

неизменных во времени токах и

узел так, что напряжения на всех

напряжениях,

называют

цепями

элементах

соединения

становятся

постоянного

тока.

Элементами

одинаковыми. Смешанное соединение —

электрических

цепей

постоянного

тока

сочетание

последовательного

являются

линейные

резисторы

параллельного

соединений.

Под

линейные источники. Резистор – элемент

преобразованием

электрической

цепи

электрической

цепи,

предназначенный

понимается такое изменение схемы и

для

использования

его

электрического

параметров ее отдельных частей, которое

сопротивления. В схемах электрических

не изменяет распределение токов и

цепей используют два типа идеальных

напряжений в оставшейся части цепи.

источников энергии – идеальный источник

напряжения (ЭДС) и идеальный источник

Б6.

Топологическое

представление

тока.

схемы электрической цепи, в которой

ветви представлены отрезками, а узлы –

Б2. Если зависимость U(I) или I(U) какого-

точками, называют графом электрической

либо

элемента

электрической

цепи

цепи. Если на графе имеется указание

линейна, то такой элемент называют

условно-положительных

направлений

линейным, а электрическую цепь,

токов ветвей в виде отрезков со

состоящую

только

из

линейных

стрелками, то такой граф называют

элементов -

линейной

цепью.

направленным

или

ориентированным

Электрическая

цепь

является

графом. Граф называют планарным, если

нелинейной, если она содержит хотя бы

его удается изобразить так, чтобы никакие

один нелинейный элемент.

две ветви не пересекались. Граф, между

Эл-ты:

Сопротивление

(резистор),

любой парой узлов которого имеется

Ёмкость

(конденсатор),

Индуктивность

ветвь или совокупность ветвей (путь),

(катушка). Активные, которые могут

называют связным.

генерировать

электрическую

энергию.

Матрица соединений (инцидентности)

Пассивные,

которые

только

потребляют

A={aij}(q-1)*p

(количество

строк

q-1,

(рассеивают или накапливают) энергию.

количество столбцов p).

Двухполюсники

бывают:

активные,

У матрицы соединений элемент аij = 1,

пассивные.

Двухполюсник,

не

если j-ая ветвь соединена с i-м узлом и 26

содержащий

внутри

себя

источников

направлена от узла, аij = –1, если j-ая

энергии называется пассивным.

ветвь соединена с i-м узлом и направлена

к этому узлу и аij = 0, если j-ая ветвь не

Б3. Закон Ома определяет связь между

соединена с i-м узлом. Матричная форма

основными

электрическими

величинами

записи первого закона Кирхгофа для

на участке

цепи

постоянного

тока

без

узлов: A*I=0

Матрица

главных

контуров

B={bij}p-(q-1)*p

активных

элементов

;

(количество

строк

p-(q-1),

количество

столбцов p). У матрицы В элемент bij = 1,

Обобщенный закон Ома определяет связь

если j-ая ветвь содержится в i-м контуре и

между

основными

электрическими

ее

направление

совпадает

обходом

величинами на участке цепи постоянного

этого

контура,

bij

–1,

если

j-ая

ветвь

тока, содержащем резистор и идеальный

содержится в i-м контуре и ее

источник ЭДС

;

Потенциальной

направление

противоположно

направлению обхода этого контура, bij = 0,

диаграммой называется

графическое

если

j-ая

ветвь

не

содержится

i-м

изображение

распределения

контуре. Матричная форма записи второго

электрического

потенциала

вдоль

закона Кирхгофа для контуров: B*U=0

замкнутого контура в зависимости от

Матрица сечений D={dij}(q-1)*p

(количество

сопротивления

участков,

входящих в

строк

q-1,

количество

столбцов

p).

выбранный контур.

матрицы сечений элемент dij = 1, если j-ая

Б4. Если в схеме двухполюсника имеются

ветвь

разрезается

i-м

сечением

ориентирована по отношению к сечению

некомпенсированные

источники,

он

так же, как и ветвь дерева,

образующая

называется

активным.

Активный

сечение,

dij

= –1, если j-ветвь разрезается

двухполюсник ведет себя

как генератор.

i-м

сечением

но

ориентирована

по

Находящиеся

внутри

него

отношению к сечению не так,

как ветвь

некомпенсированные

источники

отдают

дерева,

образующая сечение,

и dij = 0,

энергию

во

внешнюю

цепь.

схемах

если

j-ая

ветвь

не

разрезается

i-м

электрических цепей используют два типа

сечением.

Матричная

форма

записи

идеальных

источников

энергии

–

первого

закона

Кирхгофа

для

сечений:

идеальный источник напряжения (ЭДС) и

D*I=0.

Матрицы

называют

идеальный источник тока. Для идеального

топологическими

матрицами,

основное

источника напряжения (ЭДС) напряжение

свойство

этих

матриц

определяется

не зависит от тока в источнике.

соотношением A∙BТ = 0 или B∙АТ = 0.

Нагрузочная характеристика – прямая,

параллельная оси тока. Компонентное

уравнение U=Е. Схема замещения

отображает

свойства

цепи

при

определенных

условиях

облегчает

изучение процессов в ней. Схема

замещения:

источника

ЭДС

Б7.

Первый

закон

Кирхгофа:

Б10.

Метод

узловых

потенциалов

алгебраическая сумма токов ветвей,

(узловых

напряжений)

наиболее

соединенных в одном узле, равна нулю.

формализован

поэтому

часто

Уравнение, составленное по этому закону,

реализуется

машинном

анализе

имеете вид: Iк 0, причем токи,

сложных цепей. Для электрической цепи с

выходящие из узла, записывают в

q узлами можно составить q-1 уравнений

уравнении с положительным знаком, а

по первому закону Кирхгофа. Если схема

токи, входящие в узел – с отрицательным

содержит q=2 узла, то составляется одно

знаком. Необходимое и достаточное

уравнение.

количество уравнений по первому закону

1. Определить число независимых узлов

Кирхгофа равно кI=у-1, у – число узлов.

кI = (q-1), равное числу определяемых

Второй закон Кирхгофа: алгебраическая

узловых потенциалов.

сумма напряжений ветвей вдоль любого

2. Пронумеровать контура. Примем

контура

равна

нулю.

Уравнение,

потенциал любого узла (как правило, с

составленное

по

второму

закону

большим или нулевым номером) за

Кирхгофа, имеете вид: Uk 0, причем

нулевой. При наличии ветвей с

напряжения,

направления

которых

идеальным

источником

ЭДС

совпадают

направлением

обхода

рекомендуется

один

из

потенциалов

контура, берутся с положительным

граничного узла такой ветви принять за

знаком, а напряжения, направления

нулевой, тогда потенциал второго

которых

противоположны

направлению

граничного

узла считается

известным

обхода контура – с отрицательным

(особый узел).

знаком. Напряжение ветвей состоит из

3. Составить и решить узловые уравнения

напряжений

отдельных

элементов,

относительно

неизвестных

узловых

входящих в ветвь. Необходимое и

потенциалов.

Для

особых

узлов

достаточное

количество

уравнений

по

составляются особые узловые уравнения.

второму закону Кирхгофа равно кII=в-(у-1),

4. Определить токи ветвей из найденных

где в – число ветвей. Матричная форма

узловых

потенциалов

по

обобщенному

записи первого закона Кирхгофа для

закону Ома, для ветви с идеальным

узлов: A*I=0. Матричная форма записи

источником ЭДС – по первому закону

второго закона Кирхгофа для контуров:

Кирхгофа.

B*U=0. Матричная форма записи первого

Если число узлов в схеме равно двум, то

закона Кирхгофа для сечений: D*I=0.

количество уравнений, составленных по

МУП – одно. Формула двух узлов для

Б8. Для формализации математического

определения, к примеру, потенциала

описания

цепи

удобно

использовать

имеет вид: G11 1=J1(у) или

понятие обобщенной ветви, содержащей

1=( G*E+ J) / ( G)

три

типа

идеализированных элементов

цепей постоянного тока – резистор,

Б11. Для линейных электрических цепей

идеальный источник ЭДС и источник тока:

справедлив принцип наложения, согласно

Компонентное

уравнение

обобщенной

которому ток (напряжение) любой ветви

ветви (закон Ома для обобщенной ветви)

равен

сумме

частичных

токов

имеет

вид:

Uk=Rk(Ik+Jk)-Ek

или

(напряжений), создаваемых в этой ветви

Ik=Gk(Uk+Ek)-Jk.

каждым из источников в отдельности.

Частные случаи:

Этот принцип лежит в основе метода

RE – ветвь: Jk=0; Uk=RkIk-Ek; Ik=Gk(Uk+Ek)

наложения. Метод наложения применим

GJ– ветвь: Ek=0; Uk=Rk(Ik+Jk); Ik=GkUk-Jk.

только для расчета линейных цепей.

Обобщенные

ветви

позволяют

Для

удобства

использования

принципа

компонентные

уравнения

всех

типов

наложения вводят коэффициенты gij и kij,

ветвей записать в одинаковом виде, что

определяющие

связь

тока Ii со

позволяет формализовать описание цепи

значениями источников, так как при

для машинного расчета.

действии одного источника ток в линейной

цепи

пропорционален

величине

Б9. В своей основе он сводится к

источника:

составлению

уравнений

по

второму

Ii=gi1E1+gi2E2+...+ginEn+ki1J1+gi2J2+...+kimJm,

закону

Кирхгофа.

Уравнения

где gij – взаимная проводимость ветвей

составляются

не

относительно

i и j (при j=i gij=gii называют входной

напряжений ветвей, а относительно токов

проводимостью ветви i), а kij –

ветвей связи. Их называют контурные

коэффициент передачи по току между

токи. Зная токи ветвей связи, т.е.

ветвями i и j.

контурные

токи,

токи остальных

ветвей

(ветвей дерева) можно найти по первому

Б12.

Теор.

компен.

сложной

закону Кирхгофа. Число контурных токов

электрической цепи любой двухполюсник

равно числу независимых контуров кII=

с известным током может быть заменен

p(q-1).

ветвью с источником тока, равным

Определить

число

независимых

исходному и совпадающим с ним по

контуров кII= p-(q-1), равное числу

направлению. В оставшейся части схемы

неизвестных контурных токов.

токи

после

замены

останутся

2. Построить граф схемы, определить

неизменными.

ветви

дерева

ветви

связи.

В сложной электрической цепи любой

Пронумеровать

контура.

Направление

двухполюсник с известным напряжением

контурных токов и обхода контура

(или известным сопротивлением и током)

выбрать по направлению ветви связи.

может быть заменен ветвью с источником

3. При наличии особых ветвей выбрать

ЭДС, равным этому напряжению и

особые контура, состоящие из ветвей

направленным

противоположно

дерева и особой ветви. Контурный ток

напряжению ветви. В оставшейся части

особого контура известен и равен току

схемы

напряжения

после

замены

источника тока. 4. Составить и решить

останутся неизменными.

контурные

уравнения

относительно

неизвестных контурных токов. Для особых

Б13.

Электрическая

мощность

контуров составляются особые контурные

характеризует

скорость

передачи

или

уравнения. 5. Определить токи ветвей из

преобразования

электрической

энергии.

найденных контурных токов.

Равенство

мощностей

генераторов

Поэтому при наличии ветви с источником

(источников) и приемников (нагрузок)

тока

перед

формированием уравнений

называют балансом мощностей:

схему

электрической

цепи

можно

Pг = Pпр . Расчет мощности источников

эквивалентно преобразовать. Для этого

проводится следующим образом: Если

применяют несколько приемов: 1.

условно-положительные

направления

Перенос источника тока вдоль контура;

токов и напряжений на источниках

составляют

контурные

уравнения

для

выбраны соответственно рисунку, то

обобщенных ветвей.

E*I .

Мощность

приемника

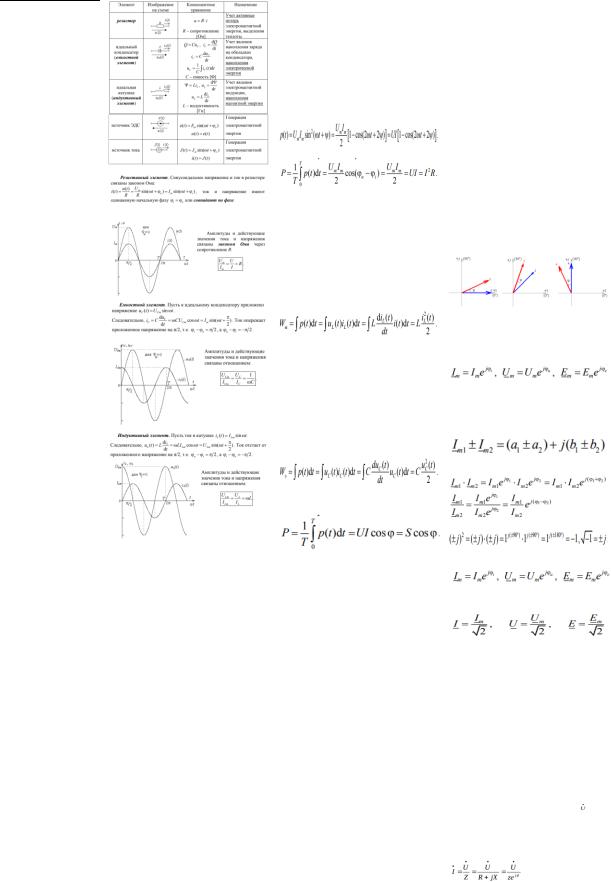
2.Компенсация тока источника токи (резистора) по формуле Джоуля-Ленца

введением эквивалентных ЭДС. Ток	равна PR = I2*R.	Таким образом, должно
источника замыкают по выбранному пути	выполняться	равенство.
(как контурный).

Б14. Суть метода эквивалентного Б17. генератора состоит в нахождении тока в одной выделенной ветви, при этом остальная часть сложной электрической цепи заменяется эквивалентным ЭДС Еэкв, с её внутренним сопротивлением

rэкв. При этом часть цепи, в которую входит источник ЭДС называют эквивалентным генератором или активным двухполюсником.

Теорема Тевенена – Гельмгольца: если активный двухполюсник, к которому присоединена выделенная ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви и сопротивлением, равным входному сопротивлению, то ток в этой ветви не изменится.

Б15. Режим, при котором в нагрузке будет выделяться максимальная мощность, называется режимом естественно передаваемой мощности или режимом согласованной работы активного двухполюсника и нагрузки.

Отношение мощности Pпр к мощности Pг называется к.п.д. эквивалентного активного двухполюсника

Б16. Токи и напряжения, мгновенные значения которых повторяются через равные промежутки времени в неизменной последовательности, называются периодическими, а наименьший промежуток времени, по истечении которого мгновенные значения повторяются называется период Т: i(t) = i(t+nТ), u(t) = u(t+nТ), где n – целое число.

В установившемся режиме в линейных цепях периодические токи и напряжения могут быть вызваны только действием источников периодических ЭДС и токов: e(t) = e(t+nТ), J(t) = J(t+nТ). При описании процессов в линейных электрических цепях все токи, напряжения и ЭДС которых изменяются по синусоидальному закону, т.е. имеют вид i(t)=Imsin( t+ i), u(t)=Umsin( t+ u), e(t)=Emsin( t+ e)

используются следующие понятия:

Im, Um, Em, – амплитуды (максимальные значения) величин i(t), u(t) и e(t);

аргументы синусоидальных функций

( t+ i), ( t+ u), ( t+ e) – фазы синусоидального тока, напряжения и ЭДС;начальные значения аргументов (начальные фазы) i , u , e тока, напряжения и ЭДС.

Б18. Для двухполюсника с напряжением

Б19. Для расчета напряжений и токов в

u(t)=Umsin( t+ u)

и током i(t)=Imsin( t+ i) ,

цепи с

синусоидальными

источниками

i мгновенной мощностью

токов и напряжений могут быть

называется

произведение

мгновенных

использованы

законы

Кирхгофа

для

значений

напряжения

тока

мгновенных значений. При дополнении

p=p(t)=u(t)*i(t), а полной мощностью –

компонентными

уравнениями

получаем

произведение действующего напряжения

полную

систему

алгебро

–

и тока S=U*I

дифференциально

–

интегральных

Мгновенная

мощность

резистора

уравнений. Для линейной цепи параметры

напряжением u(t)=Umsin( t+ u) и током

R, L и С идеализированных резистивного,

i(t)=Imsin( t+ i),

имеет

индуктивного и емкостного элементов не

постоянную

составляющую

зависят от значений и направлений токов

и напряжений

в цепи. Для

расчета

составляющую,

изменяющуюся

синусоидальных

величин

(токов,

удвоенной

частотой:

напряжений, ЭДС), т.е. для выполнения

алгебраических операций над ними,

переходят

комплексную расчетную

Активная мощность как среднее за период

область. Вращение вектора против

часовой стрелки с угловой скоростью

можно

представить

использованием

оператора поворота ej t. Поскольку все

Мгновенная мощность идеальной катушки

синусоидальные токи,

напряжения,

ЭДС

имеют одинаковую частоту , то взаимное

с напряжением u(t)=Umsin( t+ u) и током

i(t)=Imsin( t+ i)

i= /2 не имеет

расположение этих векторов в любой

постоянной составляющей:

момент времени остается неизменным, в

любой момент времени между векторами

p(t)=UmImcos( t+ i)sin( t+ i)=UIsin(2 t+2 i)

Активная

мощность,

поступающая

угол

идеальную катушку, равна нулю. Когда

p(t)>0 энергия от источника поступает в

катушку и накапливается, когда p(t)<0,

накопленная в магнитном поле энергия

отдается источнику. Энергия, запасенная

в каждый момент в магнитном поле

катушки:

Следовательно,

мгновенному

значению

тока (напряжения, ЭДС) можно поставить

Мгновенная

мощность

идеального

в соответствие комплексное число для

конденсатора

напряжением

момента

времени

t=0

( t

0).

напряжением u(t)=Umsin( t+ u) и током

Комплексные

числа

i(t)=Imsin( t+ i)

, u i=- /2 не имеет

постоянной

составляющей:

называют

комплексными

амплитудами

p(t)=UmImcos( t+ u)sin( t+ u)=UIsin(2 t+2 i

u).

Активная

мощность

идеального

соответственно тока, напряжения и ЭДС

Математические

операции

над

конденсатора

равна

нулю.

Когда

p(t)>0

комплексными числами.

энергия

от

источника

поступает

Сложение

(вычитание)

проводится в

конденсатор

накапливается в

его

алгебраической

форме

записи:

электрическом

поле,

когда

p(t)<0

накопленная энергия отдается источнику.

Запасенная

энергия

Умножение (деление) проводится в

показательной (полярной) форме записи:

Активной

мощностью

двухполюсника

называют

среднее значение мгновенной

мощности

за

период:

Для

мнимой

единицы:

Б20.

Комплексные

числа

называют

комплексными

амплитудами

соответственно тока, напряжения и ЭДС,

комплексные

числа

комплексными действующими значениями тока, напряжения и ЭДС. Введенные комплексы Im, Um , Em ( I, U, E ) однозначно описывают переменные i(t), u(t) , e(t) (существует взаимно-однозначное соответствие). Каждому комплексу Im, Um , Em ( I, U, E ) соответствует мгновенное значение синусоидального тока, напряжения и ЭДС: амплитуда равна длине (модулю) комплексной амплитуды или в корень из 2 раз больше длины (модуля) комплекса действующего значения, а начальная фазы равна углу комплексной амплитуды и комплекса действующего значения.

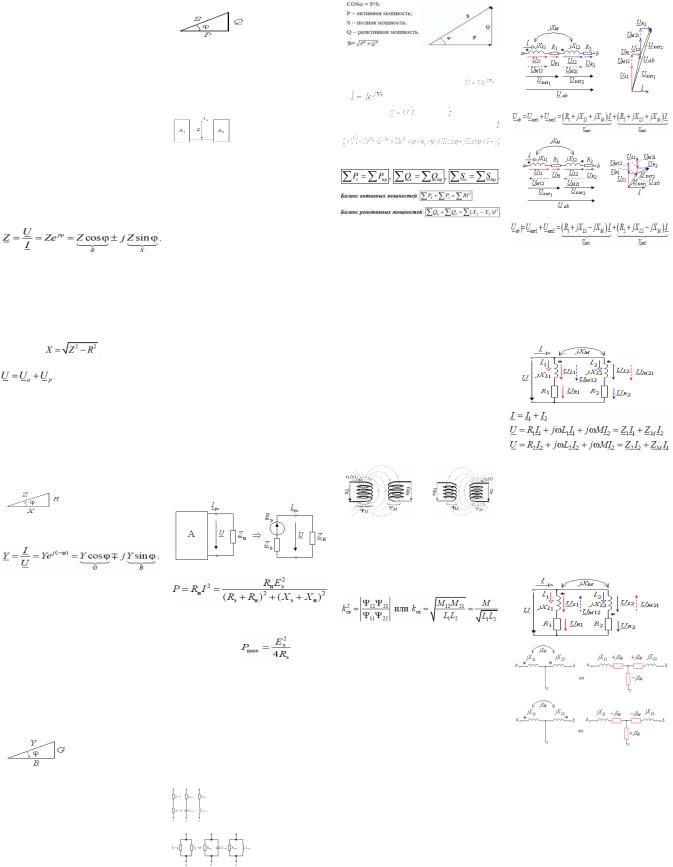
Б21.	Комплексное
сопротивление Z включено	в	цепь
переменного тока с напряжением		Точка

над буквой Z не ставится, точку принято ставить над комплексными величинами,

которые	представляют		синусоидальные
функции	времени.		Ток	в	цепи
определяется		по	закону		Ома:
		где: R –		активное
сопротивление		цепи;	X – реактивное

сопротивление цепи, которое может быть индуктивным или емкостным; z – модуль комплексного сопротивления; φ – угол сдвига по фазе.

Б22. Топографические диаграммы – это

Б24. Для участка цепи с комплексным

Б27.

Модуль

комплексной

мощности

Б30.

Различают

согласное

и встречное

изображение на

комплексной

плоскости

напряжением U U u и комплексным

равен

полной

мощности S,

активная

включение

индуктивно-связанных

точек, соответствующих концам векторов

током I I i вводят понятие комплексной

реактивная

мощности P= Re[S]=Scos ,

катушек. При согласном включении токи в

комплексных потенциалов точек схемы.

мощности. S=U*I, где I = I i комплексно-

Q Im[S]=Ssin .

Из

равенств

S=U*I,

любой момент

времени

направлены

Такая

картинка

позволяет

начертить

сопряженный вектор комплексного

тока.

P=UIcos

=UaI=UIa,

IQI=UI│sin

одинаково

относительно

одноименных

комплексные напряжения между точками,

│=UpI=UIp

зажимов,

потоки

само и взаимной

Модуль

комплексной

мощности

равен

следует,

что

стороны

треугольника

не загромождая чертёж. Такую диаграмму

индукции

сонаправлены

(напряжения

полной мощности S, активная и

напряжения

токов

пропорциональны

строят либо по результатам расчёта, либо

реактивная

мощности

Re[S]=Scos ,

мощностям и можно построить подобный

само и взаимной индукции суммируются).

качественно.

Активная

мощность

Q Im[S]=Ssin . Из равенств S=U*I,

им треугольник мощностей.

При встречном включении токи в любой

измеряется ваттметром. Ваттметр имеет

P=UIcos =UaI=UIa,

IQI=UI│sin │=UpI=UIp

Для

резистивного элемента

Sr=Pr=RI2,

момент

времени

направлены

две

цепи

(обмотки)

–

токовая

следует,

что

стороны

треугольника

противоположно

относительно

(последовательная неподвижная обмотка)

для индуктивного элемента Sl=jQl=jXlI ,

одноименных

зажимов,

потоки

само

напряжения

токов

пропорциональны

для емкостного элемента Sc=-jQc=-jXcI2

по

напряжению

(параллельная

Коэффициент мощности:

взаимной

индукции

направлены

мощностям и можно построить подобный

подвижная

обмотка). Ваттметр измеряет

противоположно

(напряжения

само

им треугольник мощностей

величину Pw=UwIwcos w, где Uw, Iw –

взаимной индукции вычитаются).

действующие значения напряжения и тока

ваттметра, а φw – угол сдвига фаз между

ними, который соответствует одинаковым

положительным

направлением

Для резистивного элемента Sr=Pr=RI2 ,

Активную, реактивную и полную мощности

комплексов

напряжения

тока

для индуктивного элемента Sl=jQl=jXlI2 ,

относительно зажимов, отмеченных * или

для емкостного элемента Sc=-jQc=-jXcI2.

можно

определить,

пользуясь

• (как правило, от отмеченных зажимов к

комплексными

изображениями

неотмеченным).

Стрелка

ваттметра

Б25. Пусть два активных двухполюсника

напряжения

тока.

Пусть

отклоняется по шкале, если w

/2 и

А1 и А2 соединены друг с другом. Пусть

Тогда

комплекс

полной

(поток

мощности

соответствует

комплекс напряжения в рассматриваемом

Согласное вкл.:

подключению прибора);

(поток

сечении U=U 0,

комплекс

тока

I=I ᴪ.

мощности:

, где

комплекс,

мощности не соответствует подключению

сопряженный

комплексом

прибора) при │ w│ /2 . Если │ w│

то

Pw 0 . Согласно

При ψ >0 ток опережает

вышесказанному,

по

показаниям

напряжение,

при

ψ<0

ток

отстает

от

Баланс

мощностей

генераторов

ваттметра

можно

определить

не

только

напряжения, при ψ =0 ток и напряжение

приемников

электромагнитной

энергии:

активную мощность, но и направление

совпадают по фазе. Если P>0, то активная

передаваемой энергии.

мощность передается от А1 к А2. По

аналогии с понятием активной мощности

Б23. Полное комплексное сопротивление

для случая Q>0, полагают, что реактивная

(входное сопротивление) двухполюсника

мощность передается от от А1 к А2, при

определяют

как

отношение

комплекса

Q<0 реактивная мощность передается от

Встречное

вкл.:

напряжения

к комплексу

входного

тока:

от А2 к А1, Q=0 нет передачи реактивной

Б28.

В том случае, если изменение тока в

мощности.

Активная

мощность

одном

из элементов цепи

приводит

измеряется ваттметром.

Ваттметр имеет

появлению ЭДС в другом элементе цепи,

две

цепи

(обмотки)

–

токовая

говорят,

что эти

элементы

индуктивно

Знак

«+»

соответствует

индуктивному

(последовательная неподвижная обмотка)

Б31.

При

параллельном соединении к

связаны,

возникающую

ЭДС

называют

характеру двухполюсника (φ >0), знак «–»

по

напряжению

(параллельная

двум неидеальным индуктивно связанным

ЭДС

взаимоиндукции.

Рассмотрим

две

емкостному

характеру

двухполюсника

подвижная

обмотка). Ваттметр измеряет

катушкам

приложено

одинаковое

катушки, которые намотаны в виде тонких

(φ <0). Активное сопротивление R=Zcos

величину Pw=UwIwcos w, где Uw, Iw –

напряжение. Пусть одноименные зажимы

колец

большого

диаметра

числом

определяют

как

отношение

активной

действующие значения напряжения и тока

витков w1 и w2. При указанной форме

находятся в общем узле.

Выберем

мощности на зажимах двухполюсника к

ваттметра, а φw – угол сдвига фаз между

катушек с большой степенью точности

условно-положительные

направления

квадрату действующего значения тока:

ними, который соответствует одинаковым

можно считать, что витки каждой катушки

тока в ветвях. Напряжение

на

катушках

R=P/I2.

Реактивное

сопротивление

положительным

направлением

сцепляются

одинаковым

магнитным

будет иметь три составляющие. Составим

X=Zsin связано соотношением Z2= R2+X2,

комплексов

напряжения

тока

потоком. Пусть в первой катушке ток i1 ,

уравнения:

относительно зажимов, отмеченных * или

тогда: Ψ11= w1Φ11 – собственное

при

этом

Напряжение

• (как правило, от отмеченных зажимов к

потокосцепление первой катушки (Φ11 –

можно

разложить

на

составляющие:

неотмеченным).

Стрелка

ваттметра

магнитный поток в одном витке), Ψ12 –

отклоняется по шкале, если w

потокосцепление

взаимной

индукции

–

Составляющую

вдоль

Pw 0 (поток мощности соответствует

часть потокосцепления Ψ11, сцепленная с

вектора тока Ua называют активной

подключению прибора); Pw 0 (поток

витками второй катушки. Ψ12 создан

составляющей

напряжения,

мощности не соответствует подключению

током первой катушки, пронизывает витки

перпендикулярную вектору тока Up –

прибора) при │ w│ /2 . Если │ w│ /2

второй. Пусть во второй катушке ток 2 i ,

реактивной

составляющей

напряжения.

, то Pw 0. Согласно вышесказанному, по

тогда: Ψ22= w2Φ22 – собственное

Вектора U, Ua и Up образуют треугольник

показаниям ваттметра можно определить

потокосцепление второй катушки, Ψ21 –

напряжений. Можно построить подобный

не только активную мощность, но и

потокосцепление

взаимной

индукции

ему треугольник сопротивлений, длины

направление

передаваемой

энергии.

(создан

током

второй

катушки,

катетов

которого

пропорциональны

Пусть приемник Zн=Rн+jXн получает

пронизывает витки первой).

этих

уравнениях

комплексные

выбранном

масштабе

активному

энергию от активного двухполюсника.

напряжения

взаимной

индукции ZмI2

реактивному

сопротивлениям,

Представим

активный

двухполюсник

ZмI1 взяты со знаком «+», т.к. токи

гипотенуза

–

полному

сопротивлению

эквивалентной

схемой

замещения

ориентированы

относительно

параметрами Eэ и Zэ=Rэ+jXэ

одноименных

зажимов

одинаково,

следовательно, напряжения само и

взаимной

индукции

имеют

одинаковое

Входной

проводимостью

называют

В таком

случае

катушки

являются

направление. Если одноименные зажимы

отношение

комплекса входного

тока

присоединены

разным узлам, то

индуктивно-связанными элементами.

для

комплексу

напряжения:

напряжения взаимной индукции при том

характеристики индуктивной связи вводят

же

выборе

условно-положительных

параметр

M=M12M21

–

взаимная

направлений

токов

будут

входить

индуктивность

[Генри].

Для

Мощность

приемника

(нагрузки)

уравнения

со

знаком

«–»:

Здесь G=Ycos – эквивалентная активная

количественной оценки

влияния

одной

катушки

на

другую

вводят

понятие

проводимость,

B=Ysin

–

коэффициента связи.

эквивалентная реактивная проводимость.

Реактивная

проводимость

может

быть

будет максимальна при Xн=-Хэ и Rн=Rэ.

положительна

отрицательна,

Таким

образом,

приемник

получает

зависимости от знака φ.

максимальную

мощность,

если Zн=Zэ.

Составляющую

вдоль

вектора

Б29.

Для

определения

направления

напряжения

называют

активной

напряжения

(ЭДС)

взаимной

индукции,

составляющей тока, а перпендикулярную

При этом условии

т.е. знака,

которым

это

напряжение

вектору

напряжения

–

реактивной

будет

входить

алгебраическую

сумму

составляющей тока. Вектора и образуют

Б26.

Существуют

различные

напряжения

на

катушке,

размечают

треугольник

тока.

Можно

построить

экспериментальные методы определения

зажимы индуктивно связанных элементов

подобный

ему

треугольник

параметров

пассивных

двухполюсников.

цепи.

Два

зажима

разных

катушек

проводимостей,

длины катетов которого

Рассмотрим

метод,

основанный

на

называют

одноименными,

если

при

пропорциональны в выбранном масштабе

измерении

тока, напряжения и

активной

одинаковых направлениях токов катушек

значениям

активной

реактивной

мощности на входе двухполюсника.

относительно

этих

зажимов

магнитные

проводимости,

гипотенуза

–

полной

Определив по приборам U, I и P, найдем

потоки

самоиндукции

взаимной

проводимости.

Z=U/I; y=I/U; r=P/I2; g=P/U2.

индукции

направлены

одинаково

Затем

вычислим

абсолютные

значения

(суммируются). Одноименные зажимы

реактивных

сопротивления

обозначаются одинаковыми значками.

проводимости

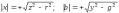Последовательная схема замещения

Параллельная схема

замещения

Б32.

простейшем

случае

Б33. Резонансом называется такой режим

Б36. При расчете электрических цепей с

Б38.

Коэффициент

формы

kф

трансформатор представляет

собой две

пассивной

цепи,

содержащей катушки

периодическими

несинусоидальными

определяется

как

отношение

индуктивно связанные катушки, которые

индуктивности и

конденсаторы,

при

токами

и напряжениями

пользуются

действующего

значения

к среднему

по

называют обмотками. Как правило,

котором

ее

входное

реактивное

разложением несинусоидальной функции

обмотки

расположены

на

общем

сопротивление

или

ее

входная

f(t) с

периодом

T в

ряд Фурье

модулю

сердечнике.

Воздушный

трансформатор

реактивная проводимость равны нулю.

Для

синусоиды

не имеет сердечника и используется: 1.

При резонансе ток на входе цепи, если он

Для развязки электрических цепей. 2. При

отличен от нуля, совпадает по фазе с

согласовании нагрузки и генератора для

напряжением. Угловая частота, при

(1.0), где

получения

максимальной

мощности

которой наступает резонанс, называется

нагрузки.

резонансной

угловой

частотой

(1.1)

Отношение напряжения на индуктивности или емкости к входному напряжению при резонансе называют добротностью контура:

Обозначим:

Коэффициент амплитуды равен отношению амплитуды к действующему

значению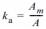 . Для синусоиды

			В электротехнике	часто пользуются	Коэффициент искажения есть отношение
			представлением f(t)	тригонометрическим
Величина	ρ	называется			действующего	значения	основной
			рядом, записанным в амплитудно-фазной
характеристическим сопротивлением цепи					гармоники к действующему значению всей
			форме:
или		контура.

Составим уравнения по второму закону
Кирхгофа для первичной и вторичной	Б34. При параллельном соединении
обмотки:	Б34. При параллельном соединении
обмотки:	резистивного, индуктивного и емкостного
	резистивного, индуктивного и емкостного
	элементов	I=Ir+IL+Ic=GU-jBLU+jBcU.

Обозначим активное сопротивление вторичного контура RII=R2+Ri, реактивное сопротивление XII=X2+Xi . Ток вторичной цепи:

Входное сопротивление трансформатора

Реактивные проводимости BL=1/ L и

Bc= C зависят от частоты, комплексная

проводимость		цепи
При	равенстве	реактивных

проводимостей BL=Bc на участке (b, c) наблюдается резонанс токов

Выделим вещественную и мнимую части

комплексного входного сопротивления:

комплексная проводимость на участке

(b,c)

Вносимое сопротивление:

сопротивление участка Zbc . При

условии BL=Bc входной ток I=Ir+IL+Ic=GU,

ток и напряжение на входе совпадают по

фазе.

Б35. В разветвленных цепях, содержащих

-активное

реактивное

вносимое

реактивные

элементы,

условием

резонанса

является

равенство

нулю

сопротивление.

Активное

вносимое

мнимой части

комплексного

входного

сопротивление

всегда

больше нуля,

сопротивления или проводимости:

реактивное имеет знак, противоположный

XII.

Требования

идеальному

трансформатору:

Активное

У разветвленной

цепи с

несколькими

сопротивление первой и второй обмоток

реактивными элементами

может

быть

должно быть минимальным:

несколько резонансных частот. Для чисто

2) Коэффициент связи или kсв=1;

реактивных

участков

может

быть

3) Реактивные сопротивления первой и

обеспечен резонанс токов или резонанс

второй

обмоток

должны

быть

напряжений. Условие резонанса для

максимально большими: L1 , L2 .

цепей,

содержащих

активные

4) Для

идеального

трансформатора

сопротивления,

определяет

также

условие

максимальной

активной

мощности, т.к. в таком случае входное

5) Комплексная мощность первичной цепи

сопротивление

оказывается

чисто

активным,

ток

напряжение

на

входе

равна комплексной мощности вторичной

совпадают по фазе, cos 1.

Энер. соот.:

цепи: S1=S2

Пусть

последовательном

Идеальный

трансформатор

колебательном

контуре R,

L, С

при

преобразует

сопротивление

нагрузки

	пропорционально квадрату коэффициента	резонансе ток равен
	трансформации без изменения аргумента
		Тогда напряжение на конденсаторе равно

кривой,

Для синусоиды kи = 1.

Коэффициент гармоник h находится как

(1.2), где

отношение

действующего

значения

высших гармоник

действующему

значению

основной

гармоники:

каждый k-й член (k = 0, 1, 2 …) ряда (1.2)

называют k-й гармоникой

Если постоянная

функции

(t).

качестве

примера

составляющая

отсутствует,

то

рассмотрим

две

несинусоидальные

функции u′ и u″ (см. 1.0). На (1.1) эти

функции

приближенно

представлены

усеченным рядом, состоящим только из

двух гармоник — первой и третьей:

u′(t) ≈ u1 + u3 = U1m sin ωt + U3m sin 3ωt,

Б39. Резонансным

режимом

работы

u″(t) ≈ u1 – u3 = U1m sin ωt – U3m sin 3ωt.

электрической

цепи

называется режим

Учет большого числа гармоник повышает

работы, при котором ток на входе

точность представления функции f(t).

совпадает с напряжением. Если на входе

Синусоидальная

функция

основной

действует

несинусоидальная

частоты называется основной или первой

периодическая ЭДС, то резонансные

гармоникой,

функция u3

тройной

частотой называется третьей гармоникой. режимы (в частности, резонанс токов или

Вобщем случае несинусоидальная напряжений) могут возникать на разных

кривая при разложении		в ряд Фурье	гармониках.		Пусть		на	вход
может	содержать	постоянную	последовательного RLC контура подается
может	содержать	постоянную	напряжение, состоящее из трех гармоник:
составляющую (нулевую гармонику) A0,			напряжение, состоящее из трех гармоник:
составляющую (нулевую гармонику) A0,
первую гармонику A1msin(ωt + ψ1)
и высшие гармоники, у которых			Индуктивность катушки может меняться
k = 2, 3, 4, …, n. Здесь k — кратность			Индуктивность катушки может меняться
k = 2, 3, 4, …, n. Здесь k — кратность			L (0; ). Для		k 1, 2,	3	действующее
частоты	гармоники	относительно	L (0; ). Для		k 1, 2,	3	действующее
частоты	гармоники	относительно
основной частоты, k > 1.
Б37. Действующее значение переменного			значение тока
тока (напряжения) определяется как			значение тока
тока (напряжения) определяется как
среднеквадратичное значение функции за
			где		. При L 0 (подставь нуль в
период	=		формулу).	При L действующее
период	=		значение тока k-ой гармоники I(k) 0.
			значение тока k-ой гармоники I(k) 0.
			Максимальное значение тока будет при
=	=	=	резонансе	напряжений		на	k 1,	2, 3
=	=	=
	. Аналогично получим		гармонике		равным			при
	. Аналогично получим
для напряжения:			выполнении		условия
			выполнении		условия
			Действующее значение тока
			На графике видно, что явления резонанса
			наблюдаются при разных значениях L на
			разных				гармониках

Суммарная энергия электрического поля

конденсатора

магнитного

поля катушки индуктивности равна

При выводе этих формул учитывалось

следующее

(при

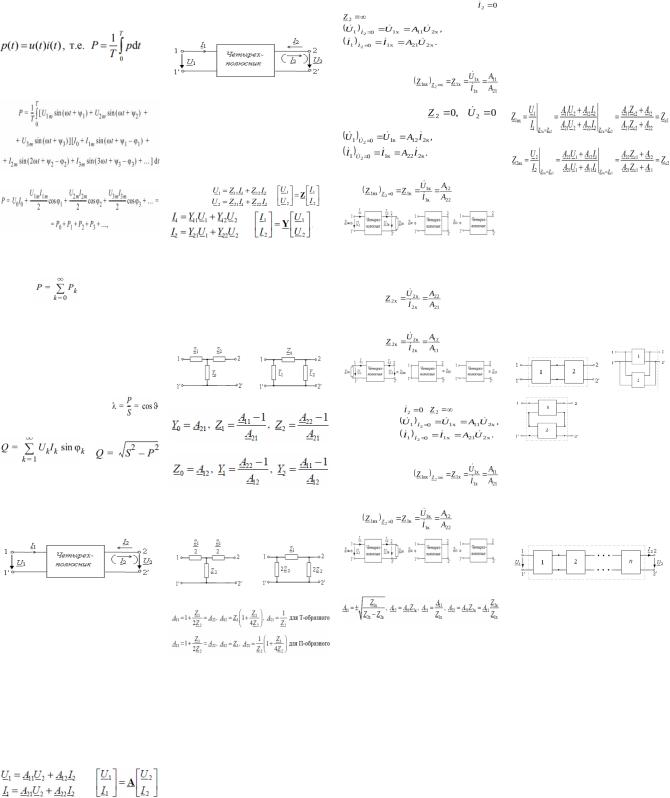
Б40.

Активная

мощность

при

Б42.

Четырехполюсники

часть

Б44.

Прямое питание.

Режим

холостого

Б46.

Вторичными

параметрами

периодическом несинусоидальном токе i и

электрической

цепи,

подключенная

хода. Принимая во внимание,

что

четырехполюсника

называются

его

напряжении u определяется как средняя

остальным участкам цепи двумя парами

характеристические сопротивления Zс1 и

формула

принимает

вид

мощность

за

период: выводов: первичных 1 – 1′ и вторичных 2 –

Zс2

постоянная

передачи

Г.

2′.

Характеристическими

называют

входные

Со

стороны

сопротивления

режиме

согласованной

1–1

нагрузки,

когда

входное

сопротивление

выводов

режиме холостого

хода

численно равно нагрузочному: Z1вх = Z2н

Выражая

несинусоидальные

токи

входное

сопротивление

(при прямом питании) и Z2вх = Z1н (при

напряжения через разложения i и u в ряд

обратном

питании).

режиме

Фурье,

получаем

интеграл

от

Если

четырехполюсник

не

содержит

четырехполюсника

согласованной

нагрузки

при

прямом

произведения двух рядов:

зависимых или

независимых источников

питании

Режим короткого замыкания. Учитывая,

энергии или эти источники взаимно

компенсируются,

то

его

называют

что

этом

случае

пассивным,

противном

случае

–

соотношение

будет

иметь

вид

активным четырехполюсником.

Активные

при

обратном

питании

четырехполюсники принято подразделять

на

автономные,

содержащие

независимые

источники

ЭДС

тока, и

Входное

сопротивление

неавтономные,

содержащие

зависимыt

После

перемножения

вычисления

четырехполюсника

со

стороны выводов

источники. Уравнения

в Z -

параметрах

Для

симметричного

четырехполюсника

интеграла

получим

Zс1=Zс2, в режиме согласованной

1–1

имеют вид:

нагрузки должно выполняется численное

равенство

Z1вх=U1/I1=U2/I2=Zн.

Сопротивление

нагрузки,

где P0, P1, P2, P3 … — соответственно

обеспечивающее

это

равенство,

называют сопротивлением согласования,

активные мощности по каждой гармонике.

Коэффициенты

уравнений

Обратное

питание

Учитывая, что при

входное

сопротивление

Таким

образом,

средняя

мощность

четырехполюсника

называются

его

обратном

питании А11иА22меняются

характеристическим

сопротивлением

несинусоидального тока за период равна

первичными параметрами. Для А-

местами,

можно

получить

еще

два

обозначают Zс . В согласованном режиме

сумме

средних

мощностей

отдельных

параметров

справедливо

уравнение

уравнения.

Входное сопротивление со

сопротивление

нагрузки

должно быть

A11A22-A12A21=1, для Z-параметров

согласовано

характеристическим

стороны выводов 2–2 в режиме холостого

Z12=Z21, Y-параметров Y12=Y21

сопротивлением четырехполюсника.

гармоник

. Для k = 0 получаем

нулевую гармонику с cosϕ0 =

Кроме

Б43. Две наиболее простые схемы

хода

Входное

Б47. Основными типами соединений

понятий

активной

мощности

вводят

замещения четырехполюсника

называют

сопротивление

четырехполюсника

со

четырехполюсников

являются

каскадное

понятие

полной

мощности

= UI. Это

Т – образной (а) и П – образной (б)

стороны выводов 2–2 в режиме короткого

(а), параллельное (б) и последовательное

связано

необходимостью

учитывать

схемами замещения.

(в) соединения.

действующие

значения

напряжений

замыкания

токов, которые характеризуют работу

электротехнических

устройств.

Отношение активной мощности Р к

полной

называют

коэффициентом

мощности λ, который иногда определяют

Для

Т-образной схемы

замещения:

Б45. Режим холостого хода. Принимая во

косинусом условного угла ϑ:

внимание,

что

формула

Иногда также условно вводят и понятие

реактивной

мощности

принимает вид

1–1 в режиме

Для П-образной схемы замещения:

Со

стороны

выводов

При замене каждого из этих соединений

холостого

хода

входное сопротивление

эквивалентным

четырехполюсником

его

Для цепей несинусоидального тока всегда

параметры могут

быть

определены

как

произведение

А-параметров

(A A1*A2)

имеет место соотношение S2≥P2 + Q2

четырехполюсника

при каскадном, как сумма Y-параметров

Б41.

Четырехполюсники

часть

Для

симметричного

четырехполюсника

Входное

сопротивление

четырехполюсника

со

стороны выводов

(Y Y1+Y2) при параллельном и как сумма

электрической

цепи,

подключенная

Z1=Z2,

Y1=Y2.

Для

симметричного

Z-параметров

(Z Z1 Z2)

при

остальным участкам цепи двумя парами

четырехполюсника

принято

таким

последовательном

соединении.

образом задавать Т- и П- образные схем

выводов: первичных 1 – 1′ и вторичных 2 –

1–1

Последовательность

каскадных

замещения:

2′.

соединений называют цепной схемой

При

расчете А-параметры можно

Если

четырехполюсник

не

содержит

определить по входным сопротивлениям

Связь А-параметров с параметрами схем

холостого хода и короткого замыкания:

зависимых или

независимых источников

Эквивалентные

А-параметры

цепи

со

замещения:

энергии

или

эти

источники

взаимно

схемой рис. 8, рассматриваемой как один

компенсируются,

то

его

называют

эквивалентной

всей

цепочке

пассивным,

противном

случае

–

Аналогично по опытам холостого хода и

четырехполюсник

определяются

как

активным четырехполюсником.

Активные

короткого

замыкания

со

стороны

матричное произведение Aц=A1*A2*...*An.

четырехполюсники принято подразделять

первичных

вторичных

выводов

Если

при

этом

если

все

на

автономные,

содержащие

определяют Z и Y-параметры. Для выбора

четырехполюсники

i=1,2,…n

имеют

независимые

источники

ЭДС

и тока,

знака A11 дополнительно определяют этот

одинаковые

А-параметры,

т.е.

неавтономные,

содержащие

зависимыt

параметр

по

опыту

холостого

хода:

A1=A2=...=An=a,

то

Aц=A*A*...*A=A

источники.

Наиболее

распространенной

A11=U1x/U2x

Отдельные четырехполюсники

называют

являются уравнения, в которых в качестве

звеньями цепной схемы.

известных (заданных) считаются ток и

напряжения

вторичных

выводов,

Б48.

Частотный электрический

фильтр

качестве

неизвестных (определяемых)

–

представляет

собой

четырёхполюсник,

ток и

напряжение

первичных.

Такие

включаемый

между

источником

уравнения

называют

«уравнения

А-

нагрузкой

для

того,

чтобы

пропускать

параметрах»,

направление

выходного

определённый спектр частот. Основными

тока I2 выбирают слева направо (на рис в

параметрами

фильтров

являются:

скобках).

Уравнения

имеют

вид:

коэффициент

затухания

а(ω)

коэффициент фазы b(ω). Фильтрами

низкой частоты (ФНЧ) называют фильтры,

,мат.

для

которых

полоса

пропускания

находится

интервале

0 c.

Замечаем,

что

уравнения

Фильтрами

высокой

частоты

(ФВЧ)

четырехполюсника при обратном питании

называют фильтры,

для которых полоса

отличаются

от

уравнений

прямого

пропускания находится в интервале

питания

местоположением

с . Граничную частоту c называют

коэффициентов А11 и А22. Отсюда условие

частотой

среза.

Полосовые

фильтры

симметричности чет.полюсников: А11 = А22

имеют полосу пропускания, ограниченную

Симметричный четырехполюсник

– это

158

частотами

среза

c2 :

четырехполюсник, в котором перемена

с1 с2, у заграждающих фильтров

местами его входных и выходных зажимов

не изменяет его входных и выходных

полоса пропускания разделена на две

токов и напряжений. A Z Y равны

части: 0 c1

и с2 . Фильтры,

для

которых

произведение продольного

сопротивления

на

соответствующее

поперечное сопротивление представляет

собой некоторое постоянное для данного

фильтра число k2 , не зависящее от

частоты,

называют

k-фильтрами.

Фильтры, для которых это произведение

зависит от частоты, называют

m-фильтрами.

Б49. Низкочастотный k-фильтр собирается из реактивных элементов по двум схемам:

Б50. Высокочастотный k-фильтр собирается из реактивных элементов по двум схемам:

Соседние файлы в папке Экзамен ИЭТ

#
12.01.20191.25 Mб29шпоры тоэ нов (1).pdf
#
12.01.20191.07 Mб27шпоры тоэ нов.docx